TOP 20 câu Trắc nghiệm Ôn tập chương 4 (Chân trời sáng tạo 2024) - Toán 10
Bộ 20 bài tập trắc nghiệm Toán lớp 10 Ôn tập chương 4 có đáp án đầy đủ các mức độ sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 10 Bài 4.
Chỉ 150k mua trọn bộ Trắc nghiệm Toán lớp 10 Chân trời sáng tạo bản word (cả năm) có đáp án chi tiết:
B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận tài liệu.
Xem thử tài liệu tại đây: Link tài liệu
Trắc nghiệm Toán 10 Ôn tập chương 4 - Chân trời sáng tạo
I. Nhận biết
Câu 1. Với điểm M(45;35), ta gọi ^xOM=α. Khẳng định nào sau đây đúng?
A. sinα=35 và cosα =45;
B. sinα=45 và cosα =35;
C. sinα=1625 và cosα =925;
D. sinα=925 và cosα =1625..
Đáp án: A
Giải thích:
Với điểm M(45;35), ta có ^xOM=α. Khi đó theo định nghĩa, ta có:
⦁ sinα = yM = 35;
⦁ cosα = xM = 45.
Vậy ta chọn phương án A.
Câu 2. Với mọi góc α thỏa mãn 0° ≤ α ≤ 180°, ta luôn có sin(90° – α) và tan(90° – α) lần lượt bằng:
A. cotα và cosα;
B. sinα và tanα;
C. cosα và cotα;
D. cosα và tanα.
Đáp án: C
Giải thích:
Với mọi góc α thỏa mãn 0° ≤ α ≤ 180°, ta luôn có:
⦁ sin(90° – α) = cosα;
⦁ tan(90° – α) = cotα.
Do đó ta chọn phương án C.
Câu 3. Với mọi góc α thỏa mãn 0° ≤ α ≤ 180°, ta luôn có cos(180° – α) bằng:
A. –cosα;
B. cosα;
C. sinα;
D. tanα.
Đáp án: A
Giải thích:
Với mọi góc α thỏa mãn 0° ≤ α ≤ 180°, ta luôn có cos(180° – α) = –cosα.
Do đó ta chọn phương án A.
Câu 4. Giá trị của tan103° bằng:
A. tan77°;
B. –tan77°;
C. cot77°;
D. –cot77°.
Đáp án: B
Giải thích:
Ta có tan103° = tan(180° – 77°) = –tan77°.
Vậy ta chọn phương án B.
Câu 5. Nếu góc α thỏa mãn 90° ≤ α ≤ 180° thì:
A. cotα > 0;
B. tanα > 0;
C. cosα > 0;
D. sinα > 0.
Đáp án: D
Giải thích:
Nếu góc α thỏa mãn 90° ≤ α ≤ 180° thì α là góc tù.
Khi đó sinα > 0, cosα < 0, tanα < 0, cotα < 0.
Do đó ta chọn phương án D.
Câu 6. Cho tam giác ABC bất kì có BC = a, AC = b và AB = c. Đẳng thức nào đúng?
A. b2 = a2 + c2 – ac.cosB;
B. a2 = b2 + c2 + 2bc.cosA;
C. c2 = b2 + a2 + ab.cosC;
D. c2 = b2 + a2 – 2ab.cosC.
Đáp án: D
Giải thích:
Theo định lí côsin ta có:
a2 = b2 + c2 – 2bc.cosA;
b2 = a2 + c2 – 2ac.cosB;
c2 = b2 + a2 – 2ab.cosC.
Do đó phương án D là đúng.
Vậy ta chọn phương án D.
Câu 7. Cho tam giác ABC có AB = c, BC = a và AC = b. Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC. Trong các mệnh đề sau, mệnh đề nào sai?
A. asinA=2R;
B. b=a.sinBsinA.
C. b = 2R.sinA;
D. c = 2R.sinC.
Đáp án: C
Giải thích:
Theo định lí sin ta có: asinA=bsinB=csinC=2R. Do đó A đúng.
Từ asinA=bsinB ta suy ra b=asinA.sinB=a.sinBsinA. Do đó B đúng.
Ta cũng có hệ quả định lí sin: b = 2R.sinB và c = 2R.sinC.
Do đó C sai và D đúng.
Vậy ta chọn phương án C.
Câu 8. Cho tam giác ABC bất kì có BC = a, AC = b và AB = c. Gọi ha, hb, hc độ dài các đường cao lần lượt ứng với các cạnh BC, CA, AB. Biết tam giác ABC có diện tích là S. Khẳng định nào sau đây là đúng?
A. ha = Sa
B. hb = 2Sb;
C. hc = S2c;
D. ha = 4Sa.
Đáp án: B
Giải thích:
Ta có công thức tính diện tích tam giác ABC là:
S = 12aha = 12bhb = chc
Do đó ta có: ha =2Sa; hb = 2Sb; hc = 2Sc
Vậy ta chọn phương án B.
Câu 9. Cho tam giác ABC bất kì có BC = a, AC = b và AB = c. Gọi R, r lần lượt là bán kính đường tròn ngoại tiếp và nội tiếp tam giác; p, S lần lượt là nửa chu vi và diện tích tam giác. Khẳng định nào sau đây là đúng?
A. S = 12abc;
B. asinA=R;
C. cosB=b2+c2−a22bc;
D. r=Sp.
Đáp án: D
Giải thích:
Theo hệ quả định lí côsin ta có: cosB=a2+c2−b22ac. Do đó C sai.
Theo định lí sin ta có: asinA=2R. Do đó B sai.
Ta có các công thức tính diện tích tam giác như sau:
• S = abc4R. Do đó A sai.
• S = pr, suy ra r=Sp. Do đó D đúng.
Vậy ta chọn phương án D.
Câu 10. Cho tam giác ABC có BC = a, AC = b và AB = c. Biết ˆC=120°. Khẳng định nào sau đây là đúng?
A. c2 = a2 + b2 – ab;
B. c2 = a2 + b2 + ab;
C. c2 = a2 + b2 – 3ab;
D. c2 = a2 + b2 + 3ab.
Đáp án: B
Giải thích:
Theo định lí côsin ta có: c2 = a2 + b2 – 2ab.cosC.
Mà ˆC=120° nên cosC = −12
Do đó c2 = a2 + b2 – 2ab.(−12) = c2 = a2 + b2 + ab.
Vậy ta chọn phương án B.
II. Thông hiểu
Câu 1. Giá trị của biểu thức B = 3 – sin290° + 2cos260° – 3tan245° bằng:
A. 2;
B.12;
C. −12;
D. 0.
Đáp án: C
Giải thích:
Ta có B = 3 – sin290° + 2cos260° – 3tan245°.
= 3 – 12 + 2.(12)2 – 3.12 = −12.
Vậy ta chọn phương án C.
Câu 2. Cho hai góc α và β (với 0° ≤ α, β ≤ 180°) thỏa mãn α + β = 180°. Giá trị của biểu thức P = sinα.cosα + sinβ.cosβ bằng:
A. 0;
B. 1;
C. –1;
D. 2.
Đáp án: A
Giải thích:
Với 0° ≤ α, β ≤ 180° và α + β = 180° ta có:
⦁ sinα = sin(180° – β) = sinβ;
⦁ cosα = cos(180° – β) = –cosβ.
Suy ra P = sinα.cosα + sinβ.cosβ
= sinβ.(–cosβ) + sinβ.cosβ
= 0.
Vậy ta chọn phương án A.
Câu 3. Giá trị của biểu thức M = sin50° + cos70° + cos110° – sin130° bằng:
A. –1;
B. 12;
C. 0;
D. 1;
Đáp án: C
Giải thích:
Ta có M = sin50° + cos70° + cos110° – sin130°
= sin50° + cos70° + cos(180° – 70°) – sin(180° – 50°)
= sin50° + cos70° – cos70° – sin50°
= (sin50° – sin50°) + (cos70° – cos70°)
= 0 + 0
= 0.
Vậy ta chọn phương án C.
Câu 4. Giá trị của biểu thức H = cot5°.cot10°.cot15°…cot80°.cot85° bằng:
A. –1;
B. 1;
C. 0;
D. 2.
Đáp án: B
Giải thích:
Ta có H = cot5°.cot10°.cot15°…cot80°.cot85°
= cot5°.cot10°.cot15°…cot(90° – 10°).cot(90° – 5°)
= cot5°.cot10°.cot15°…tan10°.tan5°
= (cot5°.tan5°).(cot10°.tan10°)…(cot40°.tan40°).cot45°
= 1.1…1.cot(45°) (Áp dụng kết quả Bài tập 5b, trang 65, Sách giáo khoa Toán 10, Tập một)
= cot45°
= 1.
Vậy ta chọn phương án B.
Câu 5. ∆ABC có AB = 3, AC = 6 và ˆA=60°. Độ dài bán kính R của đường tròn ngoại tiếp ∆ABC bằng:
A. 3;
B. 3√3;
C. √3;
D. 6.
Đáp án: A
Giải thích:
Áp dụng định lí côsin cho DABC, ta có:
BC2 = AB2 + AC2 –2.AB.AC.cosA
= 32 + 62 – 2.3.6.cos60°
= 27.
Suy ra BC=√27=3√3.
Áp dụng định lí sin, ta có BCsinA=2R.
Suy ra R=BC2.sinA=3√32.sin60°=3.
Vậy ta chọn phương án A.
Câu 6. ∆ABC có AB = 5, AC = 10, ˆA=60°. Độ dài đường cao ha của ∆ABC bằng:
A. 3√5;
B. √5;
C. 5;
D. 32.
Đáp án: C
Giải thích:
Áp dụng định lí côsin cho ∆ABC, ta có:
BC2 = AB2 + AC2 – 2AB.AC.cosA
= 52 + 102 – 2.5.10.cos60°
= 75.
Suy ra BC = = .
Diện tích ∆ABC là:
(đơn vị diện tích)
Ta có
Suy ra .
Vậy ta chọn phương án C.
Câu 7. Cho hình thoi ABCD có cạnh bằng 1 cm và có đường chéo AC = cm. Số đo bằng:
A. 30°;
B. 45°;
C. 60°;
D. 120°.
Đáp án: C
Giải thích:
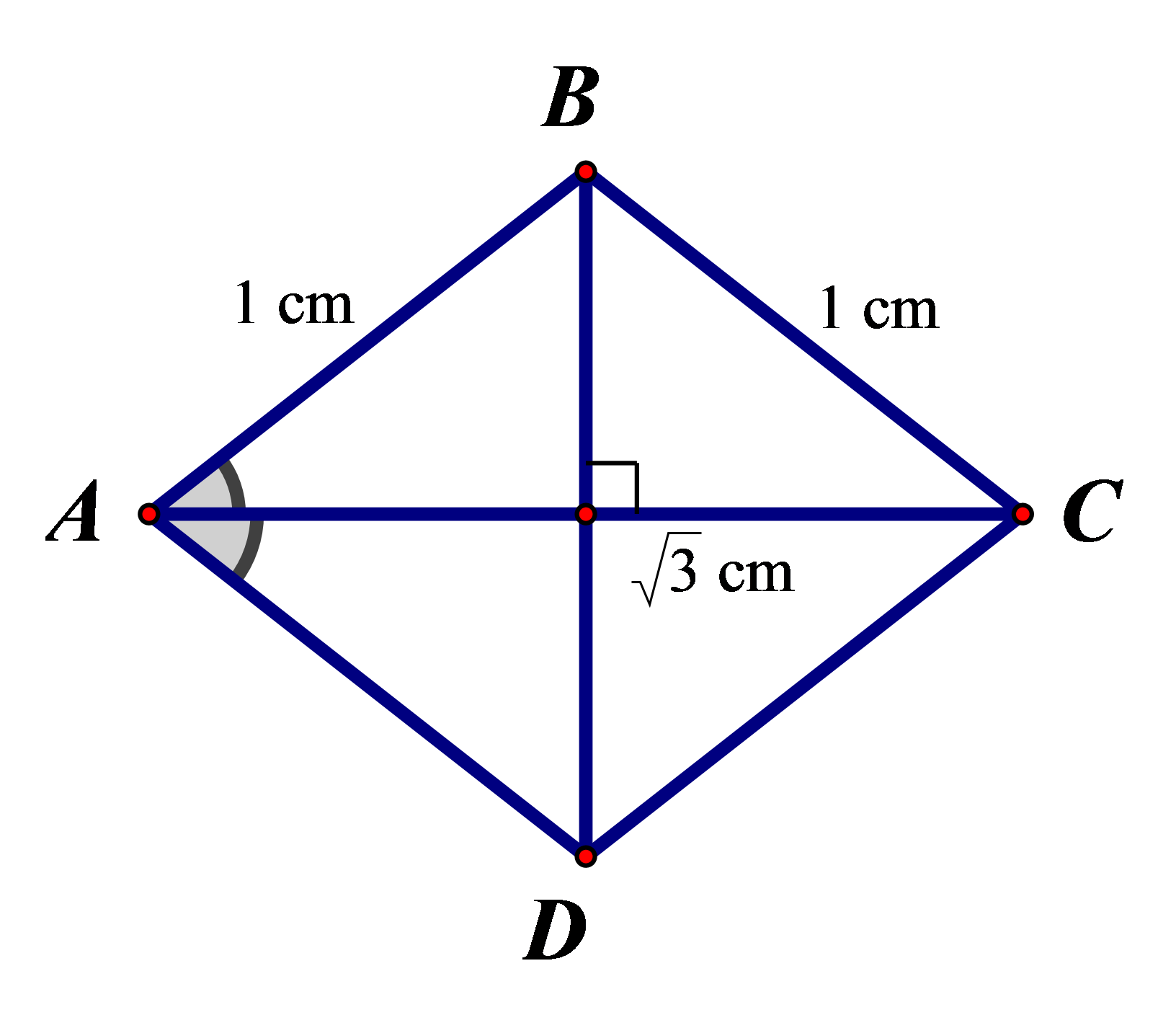
Vì ABCD là hình thoi có cạnh bằng 1 cm nên ta có AB = BC = 1 cm và AC = cm.
Áp dụng hệ quả của định lí côsin cho ABC, ta có:
.
Suy ra .
Vì ABCD là hình thoi nên đường chéo AC là tia phân giác của .
Suy ra .
Vậy ta chọn phương án C.
Câu 8. Tam giác đều nội tiếp đường tròn bán kính R = 4 cm có diện tích bằng:
A. 13 cm2;
B. cm2;
C. cm2;
D. 15 cm2.
Đáp án: C
Giải thích:
Do ∆ABC đều nên .
Áp dụng định lí sin cho ∆ABC, ta có
⇔ BC = 2R.sinA = 2.4.sin60° = .
Vì ∆ABC đều nên ta có AB = AC = BC = .
Diện tích ∆ABC là:
(cm2)
Do đó ta chọn phương án C.
Câu 9. Cho ∆ABC biết b = 32, c = 45, . Khẳng định nào sau đây đúng?
A. a ≈ 53,8, ;
B. a ≈ 2898,3, ;
C. a ≈ 53,8, ;
D. a ≈ 55,2, ;.
Đáp án: A
Giải thích:
Áp dụng định lí côsin cho DABC, ta có:
a2 = b2 + c2 – 2bc.cosA
= 322 + 452 – 2.32.45.cos87°
≈ 2898,3
Suy ra a ≈ ≈ 53,8.
Theo định lí sin, ta có
Suy ra .
Do đó
( không thỏa mãn do
∆ABC có: (định lí tổng ba góc trong một tam giác)
Suy ra .
Vậy a ≈ 53,8, .
Do đó ta chọn phương án A.
Câu 10. Cho ∆ABC, biết , , R = 6. Khẳng định nào sau đây đúng?
A. ;
B. ;
C.
D. .
Đáp án: B
Giải thích:
⦁ Theo hệ quả định lí sin, ta có:
a = 2R.sinA = 2.6.sin60° = .
⦁ Ta có S = .
Suy ra hc = b.sinA
Do đó .
⦁ Theo định lí côsin, ta có a2 = b2 + c2 – 2bc.cosA
Suy ra
Khi đó c2 – 4c – 92 = 0
Vì vậy hoặc .
Vì c là độ dài một cạnh của ∆ABC nên c > 0.
Do đó ta nhận .
Vậy ta chọn phương án B.
III. Vận dụng
Câu 1. Cho biết tanα = –3 (0° ≤ α ≤ 180°). Giá trị của bằng:
A. ;
B. ;
C. ;
D. .
Đáp án: D
Giải thích:
Vì tanα = –3 nên do đó cosα ≠ 0.
Ta có
(vì cosα ≠ 0)
.
Vậy ta chọn phương án D.
Câu 2. Cho biết sinα – cosα = (0° ≤ α, β ≤ 180°). Giá trị của bằng:
A. ;
B. ;
C. ;
D. .
Đáp án: B
Giải thích:
Ta có sinα – cosα = .
(Vì sin2α + cos2α = 1, áp dụng Bài tập 5a, trang 65, Sách giáo khoa Toán 10, Tập một)
Ta có
Vậy ta chọn phương án B.
Câu 3. Cho biết , với 0° < α < 90°. Giá trị của cotα bằng:
A. ;
B. ;
C. ;
D. .
Đáp án: D
Giải thích:
Ta có
⇒ 2sin2α = (2 – 2cosα)2
⇔ 2(1 – cos2α) = 4 – 8cosα + 4cos2α
⇔ 6cos2α – 8cosα + 2 = 0 (1)
Đặt t = cosα.
Vì 0° < α < 90° nên 0 < t < 1.
Phương trình (1) tương đương với: 6t2 – 8t + 2 = 0
Vì 0 < t < 1 nên ta nhận .
Với , ta có .
Suy ra
Áp dụng Bài tập 5a, trang 65, Sách giáo khoa Toán 10, Tập một, ta có:
sin2α + cos2α = 1
.
Vì 0° < α < 90° nên α là góc nhọn.
Do đó sinα > 0.
Vì vậy ta nhận .
Ta có .
Vậy ta chọn phương án D.
Câu 4. Cho ∆ABC và các khẳng định sau:
(I) b2 – c2 = a(b.cosC – c.cosB);
(II) (b + c)sinA = a(sinB + sinC);
(III) ha = 2R.sinB.sinC;
(IV) S = R.r.(sinA + sinB + sin C);
Số khẳng định đúng là:
A. 1;
B. 2;
C. 3;
D. 4.
Đáp án: D
Giải thích:
⦁ Ta xét khẳng định (I):
Áp dụng định lí côsin cho ∆ABC ta có:
b2 – c2 = c2 + a2 – 2ca.cosB – (a2 + b2 – 2ab.cosC)
= c2 + a2 – 2ca.cosB – a2 – b2 + 2ab.cosC
= c2 – b2 + 2a(b.cosC – c.cosB)
Þ b2 – c2 = c2 – b2 + 2a(b.cosC – c.cosB)
Þ 2(b2 – c2) = 2a(b.cosC – c.cosB)
Þ b2 – c2 = a(b.cosC – c.cosB).
Do đó khẳng định (I) đúng.
⦁ Ta xét khẳng định (II):
Áp dụng hệ quả định lí sin cho ∆ABC ta có:
(b + c)sinA =
= a(sinB + sinC).
Vì vậy khẳng định (II) đúng.
⦁ Ta xét khẳng định (III):
Áp dụng hệ quả định lí sin cho ∆ABC ta có:
2R.sinB.sinC =
.
Vì vậy khẳng định (III) đúng.
⦁ Ta xét khẳng định (IV):
Áp dụng hệ quả định lí sin cho ∆ABC ta có:
R.r.(sinA + sinB + sin C) =
.
Vì vậy khẳng định (IV) đúng.
Vậy có 4 khẳng định đúng, ta chọn phương án D.
Câu 5. Cho ∆ABC thỏa mãn . Khi đó ∆ABC là:
A. Tam giác vuông;
B. Tam giác cân;
C. Tam giác tù;
D. Tam giác đều.
Đáp án: A
Giải thích:
• Theo hệ quả của định lí côsin, ta có:
và .
• Theo hệ quả định lí sin, ta có:
.
• Ta có
⇔ sinA(cosB + cosC) = sinB + sinC
⇔ a2b + bc2 – b3 + a2c + b2c – c3 = 2b2c + 2bc2
⇔ b3 + c3 – (a2b + a2c) + (b2c + bc2) = 0
⇔ (b + c)(b2 – bc + c2) – a2(b + c) + bc(b + c) = 0
⇔ (b + c)(b2 – bc + c2 – a2 + bc) = 0
⇔ (b + c)(b2 + c2 – a2) = 0
⇔ b + c = 0 (vô lí vì b, c > 0) hoặc b2 + c2 = a2
⇔ AC2 + AB2 = BC2
Áp dụng định lí Pytago đảo, ta được ∆ABC vuông tại A.
Vậy ta chọn phương án A.
Câu 6. Cho ∆ABC có a.sinA + b.sinB + c.sinC = ha + hb + hc. Khi đó ∆ABC là:
A. Tam giác cân;
B. Tam giác đều;
C. Tam giác thường;
D. Tam giác vuông.
Đáp án: B
Giải thích:
Diện tích ∆ABC là: .
Suy ra .
Diện tích ∆ABC là:
.
Suy ra .
Ta có a.sinA + b.sinB + c.sinC = ha + hb + hc
⇔ a2 + b2 + c2 = bc + ac + ab
⇔ 2a2 + 2b2 + 2c2 = 2bc + 2ac + 2ab
⇔ (a2 – 2ab + b2) + (a2 – 2ac + c2) + (b2 – 2bc + c2) = 0
⇔ (a – b)2 + (a – c)2 + (b – c)2 = 0
⇔ a = b = c.
Vậy ∆ABC là tam giác đều.
Do đó ta chọn phương án B.
Câu 7. Từ vị trí A, người ta quan sát một cái cây cao mọc vuông góc với mặt đất như hình vẽ.
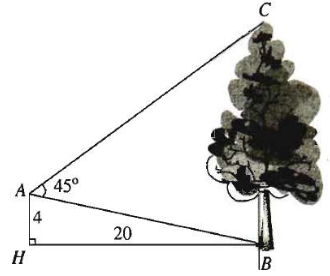
Biết vị trí quan sát cách mặt đất một khoảng AH = 4 m và khoảng cách từ chân đường vuông góc của vị trí quan sát A trên mặt đất tới gốc cây là HB = 20 m, . Chiều cao của cây gần nhất với giá trị nào sau đây?
A. 17,5 m;
B. 17 m;
C. 16,5 m;
D. 16 m.
Đáp án: A
Giải thích:
Xét ∆ABH vuông tại H có .
Suy ra .
Ta có CB ⊥ BH (cái cây vuông góc với mặt đất)
Suy ra .
Do đó
Vì vậy
∆ABC có (định lí tổng ba góc trong một tam giác)
Suy ra .
∆ABH vuông tại H nên theo định lí Pythagore ta có:
AB2 = AH2 + BH2
= 42 + 202 = 416
Suy ra AB = (m)
Áp dụng định lí sin cho ∆ABC, ta được
Suy ra
Do đó (m).
Giá trị này gần với 17,5 (m)
Vậy ta chọn phương án A.
Câu 8. Giả sử CD = h là chiều cao của tháp, trong đó C là chân tháp.
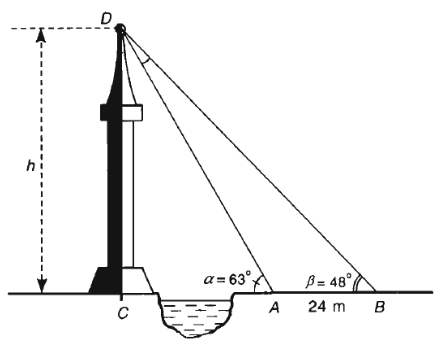
Một người đứng tại vị trí A ( không sang được bờ bên kia để đo chiều cao h của tháp nên chọn thêm một điểm B (ba điểm A, B, C thẳng hàng) cách A một khoảng 24 m và để tính toán được chiều cao của tháp. Chiều cao h của tháp gần nhất với:
A. 18 m;
B. 18,5 m;
C. 60 m;
D. 60,5 m.
Đáp án: D
Giải thích:
Ta có (hai góc kề bù).
.
∆ABD có: (định lí tổng ba góc trong một tam giác)
.
Áp dụng định lí sin cho ∆ABD, ta được
Suy ra
Do đó (m)
∆BCD vuông tại C: .
Suy ra (m)
Giá trị này gần với 60,5 m.
Vậy ta chọn phương án D.
Câu 9. Trên nóc một tòa nhà có một cột ăng-ten cao 5 m. Từ vị trí quan sát A cao 7 m so với mặt đất, có thể nhìn thấy đỉnh B và chân C của cột ăng-ten dưới góc 50° và 40° so với phương nằm ngang.
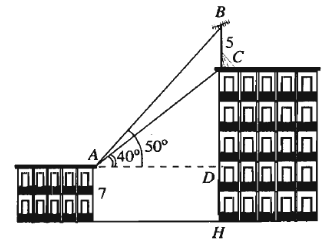
Chiều cao của tòa nhà gần nhất với giá trị nào sau đây?
A. 12 m;
B. 19 m;
C. 24 m;
D. 29 m.
Đáp án: B
Giải thích:
Ta có
Do đó .
∆ABD có: (định lí tổng ba góc trong một tam giác)
.
Áp dụng định lí sin cho ∆ABC, ta được
Suy ra (m)
∆ACD vuông tại D: .
Suy ra (m)
Chiều cao của tòa nhà là:
CH = CD + DH = 11,9 + 7 = 18,9 (m)
Giá trị này gần với 19 m nhất.
Vậy ta chọn phương án B.
Câu 10. Từ hai vị trí A và B của một tòa nhà, người ta quan sát được đỉnh C của ngọn núi. Biết rằng độ cao của tòa nhà là AB = 70 m, phương nhìn AC tạo với phương ngang AH một góc bằng 30°, phương nhìn BC tạo với phương ngang BD một góc bằng 15°30’.
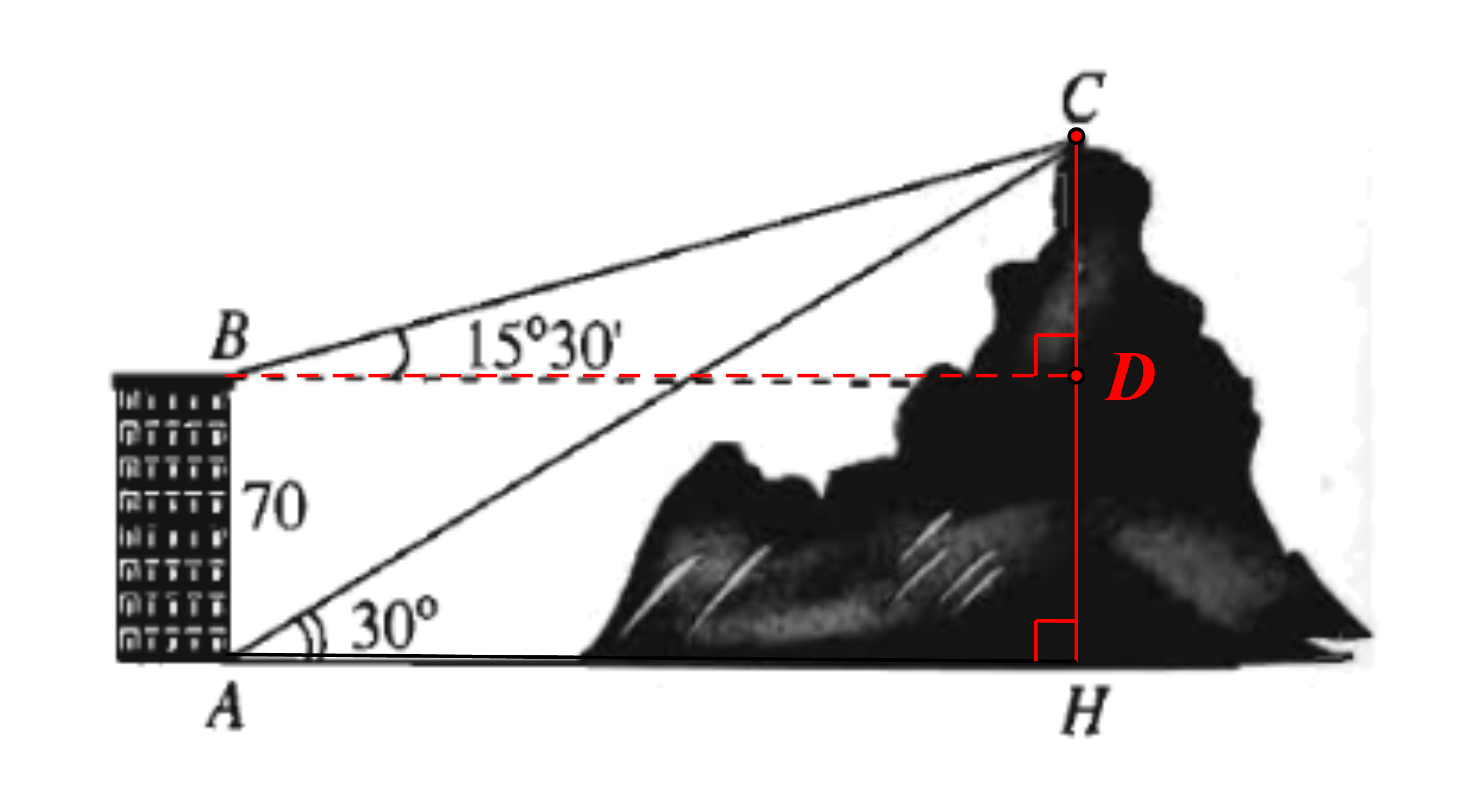
Ngọn núi đó có độ cao so với mặt đất gần nhất với giá trị nào sau đây?
A. 135 m;
B. 234 m;
C. 165 m;
D. 195 m.
Đáp án: A
Giải thích:
Ta có .
.
Ta có .
∆ABC có (định lí tổng ba góc trong một tam giác)
Suy ra .
Áp dụng định lí sin cho ∆ABC, ta được
Suy ra (m)
∆ACH vuông tại H:
Suy ra (m)
Vậy ngọn núi cao khoảng 134,7 m.
Giá trị này gần với 135 m nhất.
Do đó ta chọn phương án A.
Các câu hỏi trắc nghiệm Toán lớp 10 sách Chân trời sáng tạo có đáp án, chọn lọc khác:
Trắc nghiệm Bài 1: Giá trị lượng giác của một góc từ 0° đến 180°
Trắc nghiệm Bài 2: Bài tập Định lí côsin và định lí sin
Trắc nghiệm Bài 3: Giải tam giác và ứng dụng thực tế
Xem thêm các chương trình khác:
- Trắc nghiệm Toán lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Hóa học lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Địa Lí lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Công nghệ lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Giáo Dục Quốc Phòng lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Vật Lí lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Lịch sử lớp 10 có đáp án - Kết nối tri thức
- Trắc nghiệm Sinh học lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Tin học lớp 10 có đáp án - Kết nối tri thức
- Trắc nghiệm Kinh tế pháp luật lớp 10 có đáp án - Kết nối tri thức
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án - Global Success Kết nối tri thức
- Trắc nghiệm Hóa học lớp 10 có đáp án – Cánh Diều
- Trắc nghiệm Vật Lí lớp 10 có đáp án – Cánh Diều
- Trắc nghiệm Địa Lí lớp 10 có đáp án – Cánh Diều
- Trắc nghiệm Công nghệ lớp 10 có đáp án – Cánh Diều
- Trắc nghiệm Giáo Dục Quốc Phòng lớp 10 có đáp án – Cánh Diều
