TOP 20 câu Trắc nghiệm Dấu của tam thức bậc hai (Chân trời sáng tạo 2024) có đáp án - Toán 10
Bộ 20 bài tập trắc nghiệm Toán lớp 10 Bài 1: Dấu của tam thức bậc hai có đáp án đầy đủ các mức độ sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 10 Bài 1
Chỉ 150k mua trọn bộ Trắc nghiệm Toán lớp 10 Chân trời sáng tạo bản word (cả năm) có đáp án chi tiết:
B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận tài liệu.
Xem thử tài liệu tại đây: Link tài liệu
Trắc nghiệm Toán 10 Bài 1: Dấu của tam thức bậc hai - Chân trời sáng tạo
I. Nhận biết
Câu 1. Biểu thức nào sau đây là tam thức bậc hai?
A. f(x) = 2x3 + 3x2 + 1;
B. f(x) = –x2 + 2x – 10;
C. f(x) = x – 4;
D. f(x) = –7.
Đáp án: B
Giải thích:
Tam thức bậc hai có dạng f(x) = ax2 + bx + c, với a ≠ 0.
Ta thấy chỉ có đa thức ở phương án B có dạng f(x) = ax2 + bx + c với a = –1, b = 2 và c = –10.
Vậy ta chọn phương án B.
Câu 2. Biệt thức và biệt thức thu gọn của tam thức bậc hai f(x) = –x2 – 4x – 6 lần lượt là:
A. ∆ = –2 và ∆’ = –8;
B. ∆’ = –8 và ∆ = –2;
C. ∆ = 8 và ∆’ = 2;
D. ∆ = –8 và ∆’ = –2.
Đáp án: D
Giải thích:
Tam thức bậc hai f(x) = –x2 – 4x – 6 có dạng f(x) = ax2 + bx + c, với a = –1, b = –4, c = –6.
Biệt thức của f(x): ∆ = b2 – 4ac = (–4)2 – 4.(–1).(–6) = –8.
Biệt thức thu gọn của f(x): ∆’ = .
Vậy ∆ = –8 và ∆’ = –2.
Do đó ta chọn phương án D.
Câu 3. Nghiệm của tam thức bậc hai f(x) = –2x2 + 4x – 2 là:
A. x = 1;
B. x = 1 hoặc x = –1;
C. x = –1;
D. f(x) vô nghiệm.
Đáp án: A
Giải thích:
Tam thức bậc hai f(x) = –2x2 + 4x – 2 có ∆ = 42 – 4.(–2).(–2) = 0.
Do đó f(x) có nghiệm kép .
Vậy f(x) có nghiệm là x = 1.
Do đó ta chọn phương án A.
Câu 4. Cho f(x) = (3m – 2)x2 – 2(3m – 2)x + 3(2m + 1). Đa thức f(x) là tam thức bậc hai khi và chỉ khi:
A. ;
B. ;
C. ;
D. .
Đáp án: B
Giải thích:
Ta có đa thức f(x) = (3m – 2)x2 – 2(3m – 2)x + 3(2m + 1) là tam thức bậc hai khi và chỉ khi a ≠ 0.
Nghĩa là, 3m – 2 ≠ 0.
Suy ra .
Vậy ta chọn phương án B.
Câu 5. Cho tam thức f(x) = ax2 + bx + c (a ≠ 0), có ∆ = b2 – 4ac. Ta có f(x) ≤ 0, ∀x ∈ ℝ khi và chỉ khi:
A. a < 0 và ∆ ≤ 0;
B. a ≤ 0 và ∆ < 0;
C. a < 0 và ∆ ≥ 0;
D. a > 0 và ∆ ≤ 0.
Đáp án: A
Giải thích:
Ta có f(x) ≤ 0, ∀x ∈ ℝ khi và chỉ khi a < 0 và ∆ ≤ 0.
Ta chọn phương án A.
Câu 6. Cho f(x) = ax2 + bx + c (a ≠ 0) và ∆ = b2 – 4ac. Khi f(x) luôn cùng dấu với hệ số a, với mọi x ∈ ℝ thì:
A. ∆ < 0;
B. ∆ = 0;
C. ∆ > 0;
D. ∆ ≥ 0.
Đáp án: A
Giải thích:
Ta có f(x) cùng dấu với hệ số a với mọi giá trị của x khi ∆ < 0.
Do đó ta chọn phương án A.
Câu 7. Cho tam thức bậc hai f(x) = ax2 + bx + c (a ≠ 0). Khẳng định nào sau đây đúng?
A. Nếu ∆ > 0 thì f(x) luôn cùng dấu với hệ số a, ∀x ∈ ℝ;
B. Nếu ∆ < 0 thì f(x) luôn trái dấu với hệ số a, ∀x ∈ ℝ;
C. Nếu ∆ = 0 thì f(x) luôn cùng dấu với hệ số a, ∀x ∈ ℝ \ ;
D. Nếu ∆ < 0 thì f(x) luôn cùng dấu với hệ số b, ∀x ∈ ℝ.
Đáp án: C
Giải thích:
Cho tam thức bậc hai f(x) = ax2 + bx + c (a ≠ 0), ta có:
⦁ Nếu ∆ < 0 thì f(x) cùng dấu với a với mọi giá trị x.
Do đó phương án B, D đều sai.
⦁ Nếu ∆ = 0 và là nghiệm kép của f(x) thì f(x) cùng dấu với a với mọi x ≠ x0.
Do đó phương án C đúng.
⦁ Nếu ∆ > 0 và x1, x2 là hai nghiệm của f(x) (x1 < x2) thì f(x) trái dấu với a với mọi x trong khoảng (x1; x2); f(x) cùng dấu với a với mọi x thuộc hai khoảng (–∞; x1); (x2; +∞).
Do đó phương án A sai.
Vậy ta chọn phương án C.
II. Thông hiểu
Câu 1. Cho tam thức bậc hai f(x) = x2 – 10x + 2. Kết luận nào sau đây đúng?
A. f(–2) < 0;
B. f(1) > 0;
C. f(–2) > 0;
D. f(1) = 0.
Đáp án: C
Giải thích:
Ta có:
⦁ f(1) = 12 – 10.1 + 2 = –7 < 0.
Do đó phương án B, D sai.
⦁ f(–2) = (–2)2 – 10.(–2) + 2 = 26 > 0.
Do đó phương án C đúng, phương án A sai.
Vậy ta chọn phương án C.
Câu 2. Cho tam thức bậc hai f(x) = –2x2 + 8x – 8. Trong các mệnh đề sau, mệnh đề nào đúng?
A. f(x) < 0, ∀x ∈ ℝ;
B. f(x) ≥ 0, ∀x ∈ ℝ;
C. f(x) ≤ 0, ∀x ∈ ℝ;
D. f(x) > 0, ∀x ∈ ℝ.
Đáp án: C
Giải thích:
Tam thức bậc hai f(x) = –2x2 + 8x – 8 có ∆ = 82 – 4.(–2).(–8) = 0.
Suy ra f(x) có nghiệm kép .
Ta có a = –2 < 0.
Do đó f(x) < 0 với mọi x ≠ 2
Hay f(x) ≤ 0 với mọi x ∈ ℝ.
Do đó ta chọn phương án C.
Câu 3. Bảng xét dấu nào sau đây là của f(x) = 6x2 + 37x + 6?
A.
|
x |
–∞ –6 +∞ |
|
f(x) |
– 0 + 0 – |
B.
|
x |
–∞ –6 +∞ |
|
f(x) |
+ 0 – 0 + |
C.
|
x |
–∞ +∞ |
|
f(x) |
+ 0 + |
D.
|
x |
–∞ +∞ |
|
f(x) |
+ |
Đáp án: B
Giải thích:
Tam thức bậc hai f(x) = 6x2 + 37x + 6 có ∆ = 372 – 4.6.6 = 1225 > 0.
Do đó f(x) có hai nghiệm phân biệt là:
;
Ta có a = 6 > 0.
Ta có bảng xét dấu f(x) như sau:
|
x |
–∞ –6 +∞ |
|
f(x) |
+ 0 – 0 + |
Vậy ta chọn phương án B.
Câu 4. Cho tam thức bậc hai f(x) = x2 – 8x + 16. Khẳng định nào sau đây đúng?
A. Phương trình f(x) = 0 vô nghiệm;
B. f(x) > 0, ∀x ∈ ℝ;
C. f(x) ≥ 0, ∀x ∈ ℝ;
D. f(x) < 0 khi x < 4.
Đáp án: C
Giải thích:
Tam thức bậc hai f(x) = x2 – 8x + 16 có ∆ = (–8)2 – 4.1.16 = 0.
Do đó f(x) có nghiệm kép .
Khi đó phương án A sai.
Ta có a = 1 > 0.
Vì vậy f(x) > 0 với mọi x ≠ 4 hay f(x) ≥ 0, với mọi x ∈ ℝ.
Do đó phương án B và D sai; phương án C đúng.
Vậy ta chọn phương án C.
Câu 5. Cho tam thức bậc hai f(x) = x2 + 1. Mệnh đề nào sau đây đúng nhất?
A. f(x) > 0 ⇔ x ∈ (–∞; +∞);
B. f(x) = 0 ⇔ x = –1;
C. f(x) < 0 ⇔ x ∈ (–∞; 1);
D. f(x) > 0 ⇔ x ∈ (0; 1).
Đáp án: A
Giải thích:
Tam thức bậc hai f(x) = x2 + 1 có ∆ = 02 – 4.1.1 = –4 < 0.
Suy ra f(x) vô nghiệm.
Ta có a = 1 > 0.
Vậy f(x) > 0, ∀x ∈ ℝ hay f(x) > 0 ⇔ x ∈ (–∞; +∞).
Ta chọn phương án A.
Câu 6. Cho hàm số y = f(x) = ax2 + bx + c có đồ thị như hình vẽ.
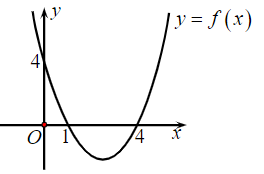
Đặt ∆ = b2 – 4ac. Chọn khẳng định đúng?
A. a > 0, ∆ > 0;
B. a < 0, ∆ > 0;
C. a > 0, ∆ = 0;
D. a < 0, ∆ = 0.
Đáp án: A
Giải thích:
Quan sát đồ thị, ta thấy:
⦁ Đồ thị y = f(x) cắt trục Ox tại hai điểm phân biệt có hoành độ lần lượt là x1 = 1; x2 = 4.
Suy ra f(x) có 2 nghiệm phân biệt x1 = 1; x2 = 4.
Do đó ∆ > 0.
⦁ Trên khoảng (–∞; 1) và (4; +∞), ta có f(x) > 0. Suy ra a > 0.
Vậy ta có a > 0, ∆ > 0.
Ta chọn phương án A.
Câu 7. Cho hàm số y = f(x) có đồ thị như hình bên.
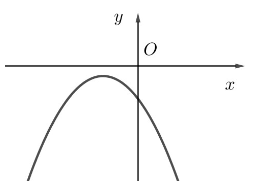
Bảng xét dấu của tam thức bậc hai tương ứng là:
A.
|
x |
–∞ +∞ |
|
f(x) |
+ |
B.
|
x |
–∞ –1 +∞ |
|
f(x) |
+ 0 + |
C.
|
x |
–∞ +∞ |
|
f(x) |
– |
D.
|
x |
–∞ –1 +∞ |
|
f(x) |
– 0 – |
Đáp án: C
Giải thích:
Quan sát đồ thị, ta thấy f(x) < 0, với mọi x ∈ ℝ.
Do đó ta có bảng xét dấu của f(x) như sau:
|
x |
–∞ +∞ |
|
f(x) |
– |
Vậy ta chọn phương án C.
Câu 8. Tam thức nào sau đây luôn dương với mọi giá trị của x?
A. f(x) = x2 – 10x + 2;
B. f(x) = x2 – 2x + 1;
C. f(x) = x2 – 2x + 10;
D. f(x) = –x2 + 2x + 10.
Đáp án: C
Giải thích:
Tam thức f(x) luôn dương với mọi giá trị của x khi và chỉ khi a > 0 và ∆ < 0.
⦁ Xét phương án A: f(x) = x2 – 10x + 2.
Ta có a = 1 > 0 và ∆ = (–10)2 – 4.1.2 = 92 > 0.
Do đó ta loại phương án A.
⦁ Xét phương án B: f(x) = x2 – 2x + 1.
Ta có a = 1 > 0 và ∆ = (–2)2 – 4.1.1 = 0.
Do đó ta loại phương án B.
⦁ Xét phương án C: f(x) = x2 – 2x + 10.
Ta có a = 1 > 0 và ∆ = (–2)2 – 4.1.10 = –36 < 0.
Do đó ta nhận phương án C.
⦁ Xét phương án D: f(x) = –x2 + 2x + 10.
Ta có a = –1 < 0.
Do đó ta loại phương án D.
Vậy ta chọn phương án C.
III. Vận dụng
Câu 1. Cho f(x) = (m – 3)x2 + (m + 3)x – (m + 1). Để f(x) là một tam thức bậc hai và có nghiệm kép thì:
A. m = 1;
B. m = –1;
C. ;
D. Cả A và C đều đúng.
Đáp án: D
Giải thích:
Xét f(x) = (m – 3)x2 + (m + 3)x – (m + 1).
Ta có:
∆ = (m + 3)2 – 4.(m – 3).[–(m + 1)]
= m2 + 6m + 9 + 4.(m – 3)(m + 1)
= m2 + 6m + 9 + 4(m2 – 2m – 3)
= 5m2 – 2m – 3.
Ta có f(x) là một tam thức bậc hai và có nghiệm kép khi và chỉ khi a ≠ 0 và ∆ = 0.
Vậy ta chọn phương án D.
Câu 2. Cho f(x) = x2 + 2(m – 1)x + m2 – 3m + 4. Giá trị của m để f(x) không âm với mọi giá trị của x là:
A. m < 3;
B. m ≥ 3;
C. m ≤ –3;
D. m ≤ 3.
Đáp án: D
Giải thích:
Xét f(x) = x2 + 2(m – 1)x + m2 – 3m + 4.
Ta có:
∆’ = (m – 1)2 – 1.(m2 – 3m + 4)
= m2 – 2m + 1 – m2 + 3m – 4
= m – 3.
Yêu cầu bài toán ⇔ Tìm m để f(x) ≥ 0 với mọi giá trị của x.
Ta có f(x) ≥ 0, với mọi giá trị của x.
⇔ a > 0 và ∆’ ≤ 0.
⇔ 1 > 0 (luôn đúng) và m – 3 ≤ 0.
⇔ m ≤ 3.
Vậy m ≤ 3 thỏa mãn yêu cầu bài toán.
Ta chọn phương án D.
Câu 3. Cho f(x) = mx2 – 2mx + m – 1. Giá trị nào của m để f(x) ≥ 0 vô nghiệm?
A. m ≤ 0;
B. m ≥ 0;
C. m < 0;
D. m > 0.
Đáp án: C
Giải thích:
Nếu m = 0 ta có f(x) = –1 < 0 khi đó f(x) ≥ 0 vô nghiệm.
Do đó m = 0 thỏa mãn yêu cầu đề bài.
Nếu m ≠ 0 thì f(x) = mx2 – 2mx + m – 1 là tam thức bậc hai.
Ta có:
∆’ = (–m)2 – m.(m – 1)
= m2 – m2 + m
= m.
Ta có f(x) ≥ 0 vô nghiệm. Nghĩa là, f(x) < 0, với mọi giá trị của x.
⇔ a < 0 và ∆’ < 0
⇔ m < 0 và m < 0
⇔ m < 0.
Vậy m ≤ 0 thỏa mãn yêu cầu bài toán.
Ta chọn phương án A.
Câu 4. Cho f(x) = ax2 + bx + c (a ≠ 0) có đồ thị đi qua ba điểm (0; 1); (1; –2); (3; 5). Kết luận nào sau đây đúng?
A. f(x) âm trong khoảng ;
B. f(x) âm trong khoảng ;
C. f(x) âm trong khoảng (3; +∞);
D. f(x) dương trong khoảng .
Đáp án: A
Giải thích:
Xét f(x) = ax2 + bx + c (a ≠ 0):
⦁ Ta có đồ thị đi qua điểm (0; 1) nên f(0) = 1.
Khi đó a.02 + b.0 + c = 1.
Vì vậy c = 1.
⦁ Ta có đồ thị đi qua điểm (1; –2) nên f(1) = –2.
Khi đó a.12 + b.1 + c = –2.
Vì vậy a + b + c = –2 (1)
Thế c = 1 vào (1) ta được a + b + 1 = –2.
Do đó a = –b – 3.
⦁ Ta có đồ thị đi qua điểm (3; 5) nên f(3) = 5.
Khi đó a.32 + b.3 + c = 5.
Vì vậy 9a + 3b + c = 5 (2)
Thế c = 1 và a = –b – 3 vào (2) ta được 9(–b – 3) + 3b + 1 = 0.
Suy ra –9b – 27 + 3b + 1 = 0.
Do đó –6b – 26 = 0.
Vì vậy .
Với , ta có a = –b – 3 = > 0.
Vậy ta có tam thức bậc hai .
Ta có ∆ = > 0.
Suy ra f(x) có 2 nghiệm phân biệt là:
Ta có bảng xét dấu của f(x) như sau:
|
x |
–∞ 3 +∞ |
|
f(x) |
+ 0 – 0 + |
Vậy f(x) âm trong khoảng và f(x) dương trong hai khoảng và (3; +∞).
Ta chọn phương án A.
Câu 5. Cho f(x) = mx2 + 2(m + 1)x + m – 2. Với giá trị nào của tham số m thì f(x) là tam thức bậc hai và f(x) > 0 có nghiệm?
A. m ∈ ℝ;
B. ;
C. m ∈ ;
D. m ∈ ℝ \ {0}.
Đáp án: C
Giải thích:
f(x) = mx2 + 2(m + 1)x + m – 2 là tam thức bậc hai ⇔ a ≠ 0 ⇔ m ≠ 0.
Ta có:
∆’ = (m + 1)2 – m(m – 2)
= m2 + 2m + 1 – m2 + 2m
= 4m + 1.
Trường hợp 1: a > 0 ⇔ m > 0.
Khi đó f(x) > 0 có nghiệm với mọi x.
Do đó m > 0 thỏa mãn yêu cầu đề bài.
Trường hợp 2: a < 0 ⇔ m < 0.
Khi đó để f(x) > 0 có nghiệm thì ∆ > 0.
⇔ 4m + 1 > 0.
⇔ .
Kết hợp m < 0 ta có
Kết hợp cả 2 trường hợp, ta thu được kết quả m ∈ .
Vậy m ∈ thỏa mãn yêu cầu bài toán.
Ta chọn phương án C.
Các câu hỏi trắc nghiệm Toán lớp 10 sách Chân trời sáng tạo có đáp án, chọn lọc khác:
Trắc nghiệm Bài 2: Giải phương trình bậc hai một ẩn
Trắc nghiệm Bài 3: Phương trình quy về phương trình bậc hai
Xem thêm các chương trình khác:
- Trắc nghiệm Toán lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Hóa học lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Địa Lí lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Công nghệ lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Giáo Dục Quốc Phòng lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Vật Lí lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Lịch sử lớp 10 có đáp án - Kết nối tri thức
- Trắc nghiệm Sinh học lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Tin học lớp 10 có đáp án - Kết nối tri thức
- Trắc nghiệm Kinh tế pháp luật lớp 10 có đáp án - Kết nối tri thức
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án - Global Success Kết nối tri thức
- Trắc nghiệm Hóa học lớp 10 có đáp án – Cánh Diều
- Trắc nghiệm Vật Lí lớp 10 có đáp án – Cánh Diều
- Trắc nghiệm Địa Lí lớp 10 có đáp án – Cánh Diều
- Trắc nghiệm Công nghệ lớp 10 có đáp án – Cánh Diều
- Trắc nghiệm Giáo Dục Quốc Phòng lớp 10 có đáp án – Cánh Diều
