Lý thuyết Tia phân giác của một góc và cách giải các dạng bài tập (chính xác nhất)

Lý thuyết Tia phân giác của một góc và cách giải các dạng bài tập (chính xác nhất)

I. Lý thuyết tia phân giác

1. Tia phân giác là gì?

Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.

Ví dụ:

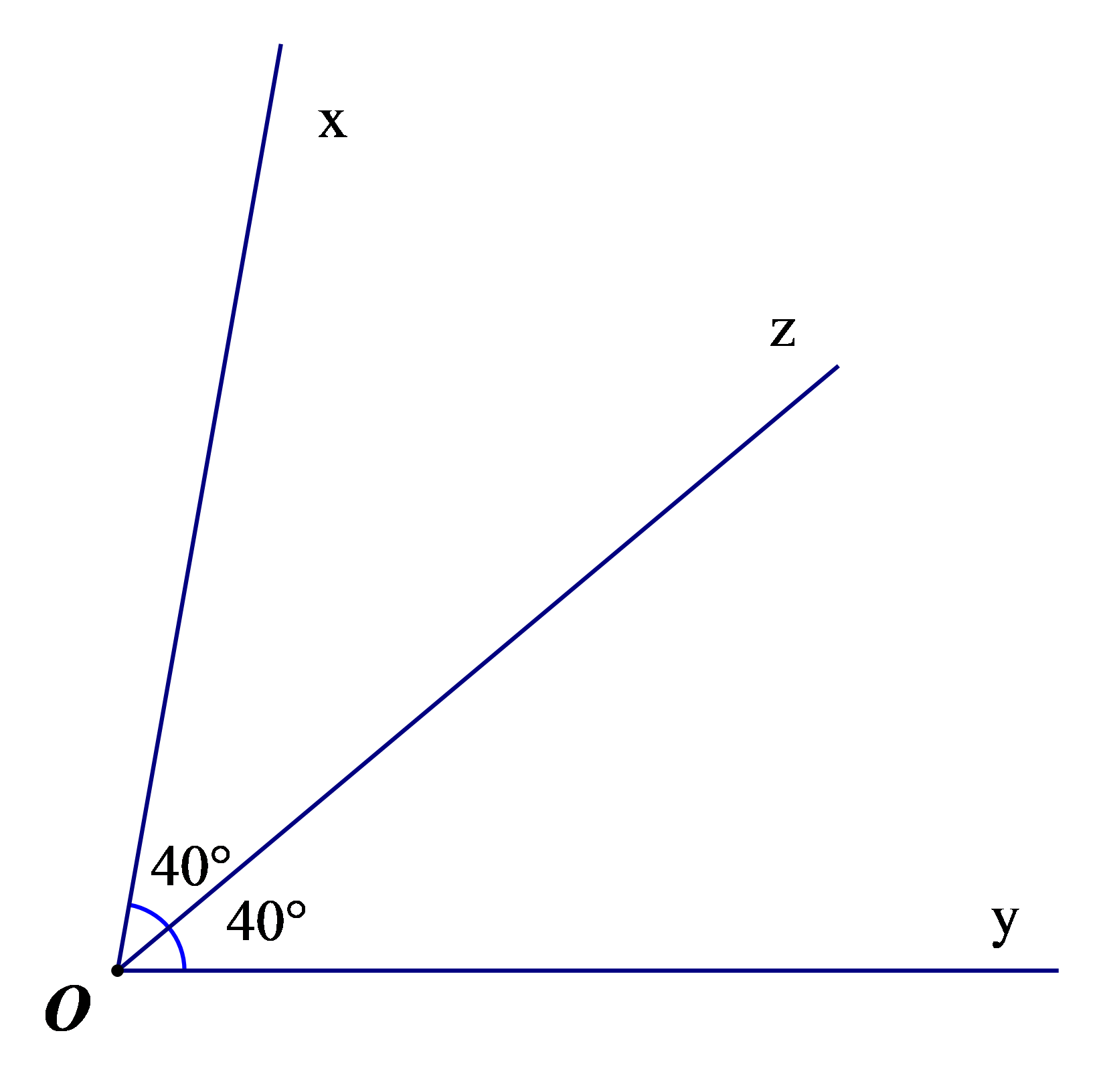Ta thấy tia Oz nằm trong góc xOy và tia Oz tạo với cạnh Ox góc xOz, tạo với cạnh Oy góc yOz; hai góc xOz và yOz đều bằng 40°.

Vì vậy, tia Oz là tia phân giác của góc xOy.

2. Vẽ tia phân giác của một góc

Cho góc xOy. Để vẽ tia phân giác của góc xOy ta có các cách sau:

Cách 1: Vẽ tia phân giác của một góc bằng thước thẳng và compa.

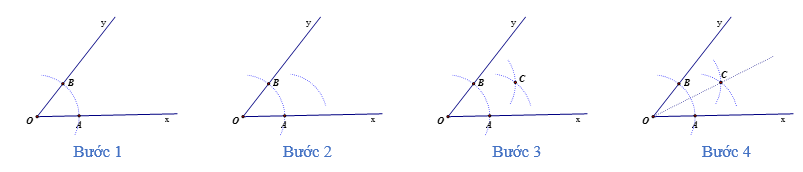
Bước 1: Trên tia Ox lấy điểm A bất kì (A khác O). Vẽ một phần đường tròn tâm O bán kính OA, cắt tia Oy tại điểm B.

Bước 2: Vẽ một phần đường tròn tâm A bán kính AO.

Bước 3: Vẽ một phần đường tròn tâm B bán kính AO, cắt phần đường tròn tâm A bán kính AO tại điểm C nằm trong góc xOy.

Bước 4: Vẽ tia OC, ta được tia phân giác của góc xOy.

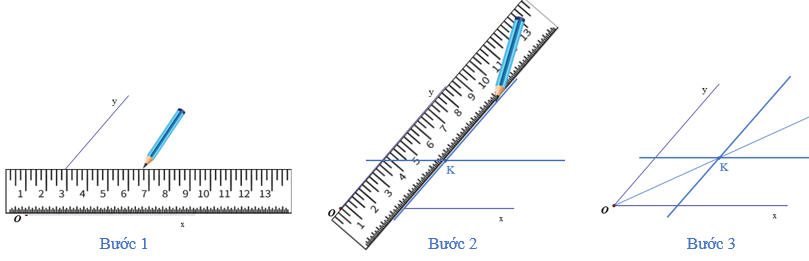
Cách 2: Dùng thước hai lề

Bước 1: Đặt thước hai lề sao cho một cạnh của thước trùng với một trong hai cạnh của góc xOy; dùng bút, vạch một vạch thẳng theo cạnh kia của thước.

Bước 2: Đặt thước hai lề sao cho một cạnh của thước trùng với cạnh còn lại của góc xOy; dùng bút, vạch một vạch thẳng theo cạnh kia của thước.

Bước 3: Hai nét vạch ở bước 1 và bước 2 cắt nhau tại điểm K nằm trong góc xOy. Vẽ tia OK, ta được tia này là tia phân giác của góc xOy.

3. Định lí tia phân giác

* Định lý thuận:

Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.

* Định lí đảo:

- Điểm nằm bên trong một góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.

- Tập hợp các điểm nằm bên trong một góc và cách đều hai cạnh của góc là tia phân giác của góc đó.

II. Đường phân giác

1. Đường phân giác là gì?

- Đường phân giác của một góc chia góc đó thành hai góc có độ lớn bằng nhau.

- Mọi điểm trên một đường phân giác cách đều hai cạnh của góc đó và ngược lại.

2. Tính chất đường phân giác trong tam giác

Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.

* Lưu ý: Định lí vẫn đúng với tia phân giác của góc ngoài của tam giác.

III. Sự khác biệt giữa tia phân giác và đường phân giác

Tia Phân Giác: Là một tia bắt đầu từ đỉnh của một góc và chia góc đó thành hai góc bằng nhau. Tia phân giác không phải là đoạn thẳng có độ dài xác định mà là một phần của đường thẳng vô hạn.

Đường Phân Giác: Trong một tam giác, đường phân giác là đoạn thẳng nối từ một đỉnh tam giác đến điểm cắt của tia phân giác với cạnh đối diện. Đường phân giác là một đoạn thẳng có độ dài xác định và chia cạnh đối diện tam giác theo tỷ lệ nhất định.

Mối Quan Hệ: Tia phân giác là thành phần cơ bản có thể dựa vào từ đó xác định đường phân giác. Đường phân giác chính là đoạn thẳng mà tia phân giác cắt cạnh đối diện tam giác, và nó chia cạnh đối diện thành hai phần tương ứng.

IV. Bài tập tự luyện

1 Bài tập tự luận

Bài 1. Cho góc xAm có số đo bằng 65° và tia Am là tia phân giác của xAy. Tính số đo góc xAy.

Hướng dẫn giải

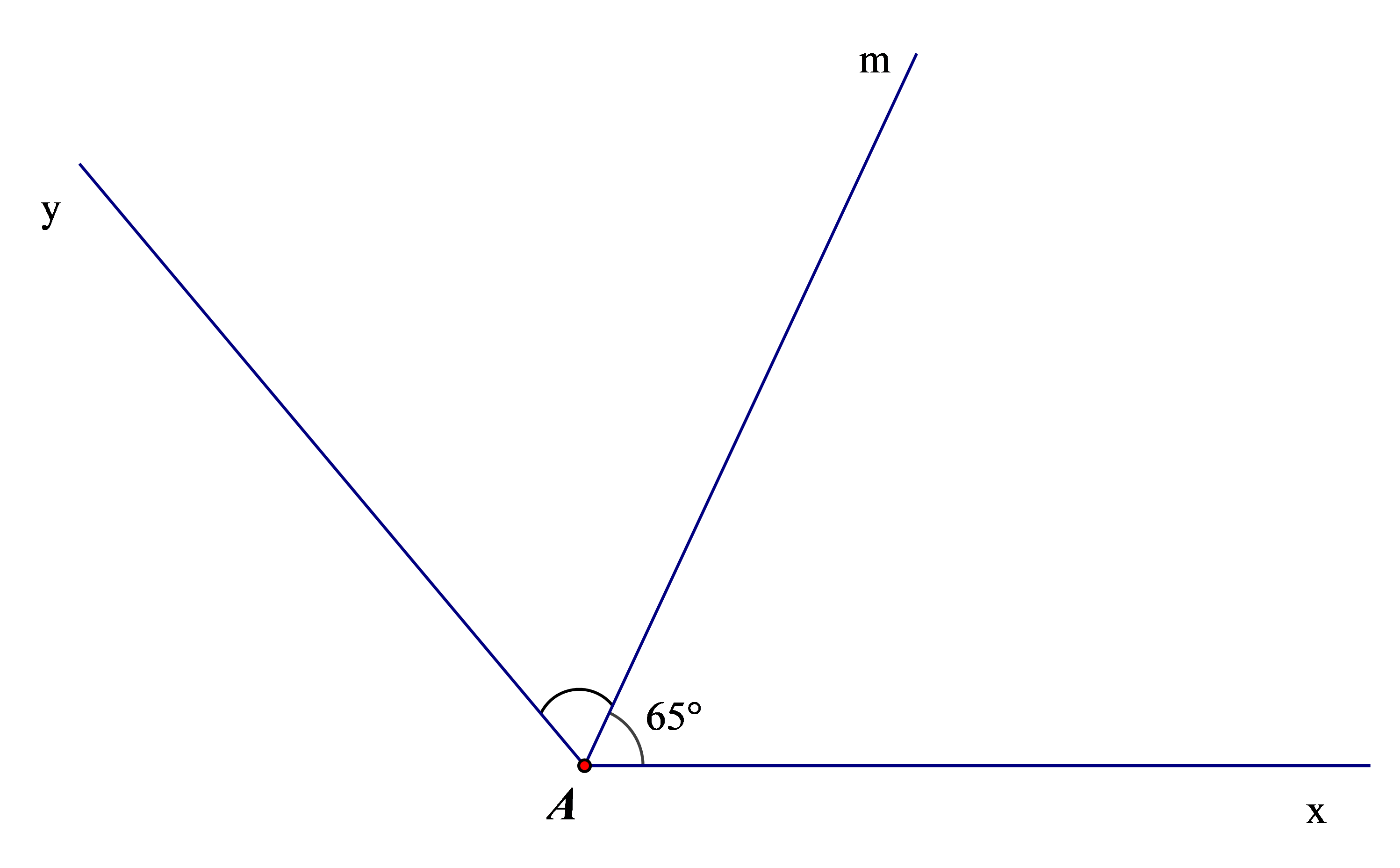Vì Am là tia phân giác của góc xAy nên:

Ta có $\widehat{xAy}=2.\widehat{xAm}=2.65°=130°$.

Vậy $\widehat{xAy}=130°$.

Bài 2. Cho góc xOy có số đo bằng 110°. Tia Oz là tia phân giác của góc xOy. Tính số đo các góc xOz và yOz.

Hướng dẫn giải

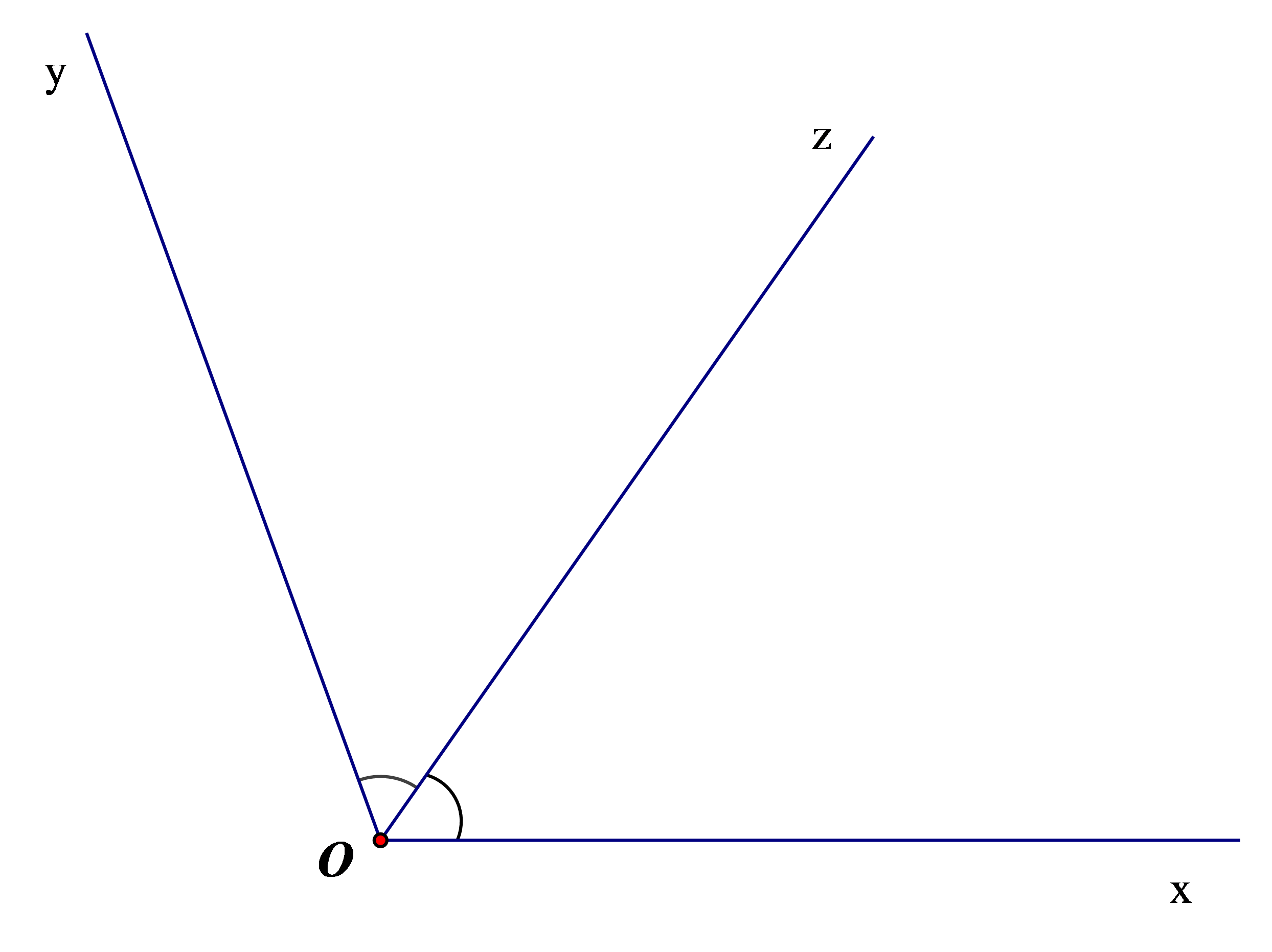Vì tia Oz là tia phân giác của góc xOy nên:

Ta có $\widehat{xOz}=\widehat{yOz}=\widehat{xOy}:2=110°:2=55°$.

Vậy $\widehat{xOz}=\widehat{yOz}=55°$.

2 Bài tập trắc nghiệm

Câu 1. Cho $\widehat{HOK}=90°$ và tia OI sao cho tia OK là tia phân giác của góc HOI. Khi đó góc HOI là:

A. góc vuông;

B. góc nhọn;

C. góc tù;

D. góc bẹt.

Hướng dẫn giải

Đáp án đúng là: B

Ta có: OK là tia phân giác của góc HOI $\Rightarrow \widehat{HOK}=\widehat{KOI}=90°$.

$\Rightarrow \widehat{HOI}=\widehat{HOK}+\widehat{KOI}=90°+90°=180°$.

Vậy góc HOI là góc bẹt.

Câu 2. Tính góc xOt, biết góc xOy và góc x'Oy' là hai góc đối đỉnh, $\widehat{x\text{'}Oy\text{'}}=60°$ và tia Ot là tia phân giác góc xOy.

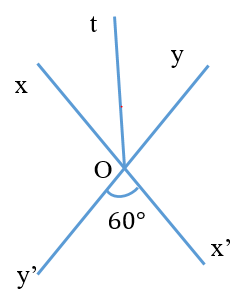
A. 60°;

B. 120°;

C. 42°;

D. 30°.

Hướng dẫn giải

Đáp án đúng là: D

Ta có góc xOy và góc x'Oy' là hai góc đối đỉnh $\Rightarrow \widehat{xOy}=\widehat{x\text{'}Oy\text{'}}=60°$.

Mà Ot là tia phân giác góc xOy $\Rightarrow \widehat{xOt}=\widehat{yOt}=\frac{\widehat{xOy}}{2}=\frac{60°}{2}=30°$.

Vậy góc $\widehat{xOt}=30°$.

Câu 3. Cho các thông số như hình vẽ, Ot là tia phân giác góc zOx. Tính số đo góc zOt.

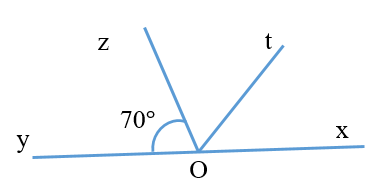A. 65°;

B. 40°;

C. 55°;

D. 110°.

Hướng dẫn giải

Đáp án đúng là: C

Ta có: góc yOz và góc zOx là hai góc kề bù $\Rightarrow \widehat{yOz}+\widehat{zOx}=180°$

$\Rightarrow \widehat{zOx}=180°-\widehat{yOz}=180°-70°=110°$.

Mà Ot là tia phân giác của góc zOx nên $\widehat{zOt}=\widehat{xOt}=\frac{\widehat{zOx}}{2}=\frac{110°}{2}=55°$.

Xem thêm tóm tắt lý thuyết Toán lớp 7 sách Cánh diều hay, chi tiết khác:

Lý thuyết Bài tập ôn tập chương 3

Lý thuyết Bài 1. Góc ở vị trí đặc biệt