Giải sbt Toán 9 (Kết nối tri thức) Bài tập cuối chương 4 trang 50

Giải SBT Toán 9 Bài tập cuối chương 4 trang 50

A. Trắc nghiệm

Bài 1 trang 50 sách bài tập Toán 9 Tập 1: Tam giác ABC vuông tại A thì:

A. sin B + cos C = 0.

B. sin C + cos B = 0.

c. sin B – cos C = 0.

D. cos B + cos C = 0.

Lời giải:

Đáp án đúng là: C

Tam giác ABC vuông tại A nên hai góc B và C là hai góc phụ nhau, do đó sin B = cos C hay sin B – cos C = 0.

Bài 2 trang 50 sách bài tập Toán 9 Tập 1: Tam giác ABC vuông tại A thì:

A. tan B + tan C = 0.

B. tan B + cot C = 0.

C. tan B – cot C = 0.

D. cot B + cot C = 0.

Lời giải:

Đáp án đúng là: C

Tam giác ABC vuông tại A nên hai góc B và C là hai góc phụ nhau.

Do đó tan B = cot C hay tan B – cot C = 0.

Bài 3 trang 51 sách bài tập Toán 9 Tập 1: Chọn câu sai:

Góc nhọn α có sin α = $\frac{1}{2}$ thì

A. $\frac{1}{\tan \alpha }=\sqrt{3}$

B. $\frac{1}{\sin \alpha }=2$

C. ${\tan }^2\alpha =\frac{1}{3}$

D. ${\cos }^2\alpha =\frac{1}{4}$

Lời giải:

Đáp án đúng là: D

Ta có: ${\cos }^2\alpha =1-{\sin }^2\alpha =1-{\left(\frac{1}{2}\right)}^2=\frac{3}{4}\ne \frac{1}{4}$ nên đáp án D sai.

• B. Tự luận

  • Bài 4.28 trang 51 sách bài tập Toán 9 Tập 1:

    Chứng minh nếu một góc nhọn của một tam giác vuông có số đo gấp đôi số đo góc nhọn kia thì tam giác đó có một cạnh dài gấp đôi một trong hai cạnh còn lại.

    Lời giải:

    Xét tam giác ABC vuông tại A có $\widehat{B}=2\widehat{C}$

    Ta có: $\widehat{B}+\widehat{C}=90°$

    $\widehat{C}+2\widehat{C}=90°$

    $3\widehat{C}=90°$

    $\widehat{C}=30°$

    Tam giác ABC vuông tại A có:

    $\frac{AB}{BC}=\sin C=\sin 30°=\frac{1}{2}$ hay BC = 2AB.

    Vậy nếu một góc nhọn của một tam giác vuông có số đo gấp đôi số đo góc nhọn kia thì tam giác đó có một cạnh dài gấp đôi một trong hai cạnh còn lại.

  • Bài 4.29 trang 51 sách bài tập Toán 9 Tập 1: Xét điểm B nằm giữa hai điểm A và H. Giả sử có điểm D sao cho DH vuông góc với AB và $\widehat{DAH}$ = 15°, $\widehat{DBH}$ = 30°. Chứng minh rằng $HD=\frac{AB}{2}$.

    Lời giải:

    

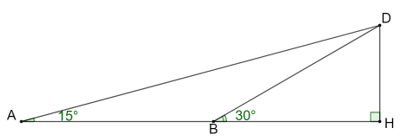
    Xét tam giác HBD vuông tại H, ta có:

    $\frac{HD}{BD}=\sin \widehat{DBH}=\sin 30°=\frac{1}{2}$, suy ra $\frac{HD}{BD}=\frac{1}{2}$ hay BD = 2HD.

    Xét tam giác ABD ta có:

    $\widehat{ABD}=180°-\widehat{BDH}=180°-30°=150°$

    $\widehat{BDA}=180°-\widehat{BAD}-\widehat{ABD}=180°-150°-15°=15°$

    Suy ra $\widehat{BAD}=\widehat{BDA}$, hay tam giác ABD cân tại B.

    Do đó AB = BD = 2HD hay $HD=\frac{AB}{2}$(đpcm).

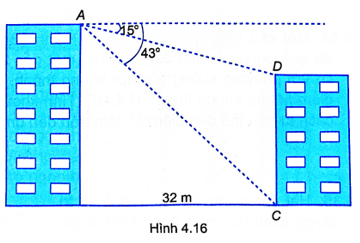
  • Bài 4.30 trang 51 sách bài tập Toán 9 Tập 1: Cho hai toà nhà cách nhau 32 m. Tại điểm A trên nóc toà nhà cao nhìn xuống nóc D và chân C của toà nhà thấp lần lượt theo các góc 15° và 43° (so với phương nằm ngang) (H.4.16). Tính chiều cao của hai toà nhà đó (lảm tròn đến m).

    

    Lời giải:

    

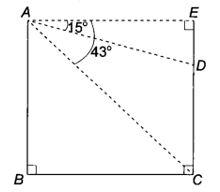
    Gọi điểm B là vị trí chân tòa nhà cao.

    Theo đề bài, ta có: BC = 32 m, $\widehat{EAC}=43°, \widehat{DAE}=15°$

    Do AE // BC nên $\widehat{EAC}=\widehat{ACB}=43°$

    Xét tam giác ABC vuông tại B ta có:

    $AB=BC.\tan \widehat{ACB}=32.\tan 43°\approx 30$ (m)

    Xét tam giác DEA vuông tại E ta có:

    $ED=EA.\tan \widehat{EAD}=32.\tan 15°\approx 9$(m)

    CD = CE – ED = AB – ED ≈ 30 – 9 = 21 (m)

    Vậy tòa nhà cao cao xấp xỉ 30 m và tòa nhà thấp cao xấp xỉ 21 m.

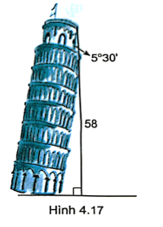
  • Bài 4.31 trang 51 sách bài tập Toán 9 Tập 1: Chiều cao từ mặt đất đến đỉnh tháp Pisa ở Italia là 58 mét, tháp nghiêng góc 5°30' đối với phương thẳng đứng (H.4.17). Khi Mặt Trời chiếu vuông góc với mặt đất thì bóng của tháp dài bao nhiêu decimét.

    

    Lời giải:

    

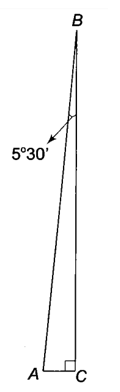
    Gọi A là chân tháp, B là đỉnh tháp và C là vị trí bóng của đỉnh tháp.

    Theo đề bài, ta có: BC = 58 m, $\widehat{ABC}=5°{30}^{\text{'}}$.

    Xét tam giác ACB vuông tại C ta có:

    $AC=BC\cdot \tan B=58\cdot \tan 5°{30}^{\text{'}}\approx \mathrm{5,6}$ (m) = 56 (dm).

    Vậy bóng của tháp dài xấp xỉ 56 dm.

  • Bài 4.32 trang 52 sách bài tập Toán 9 Tập 1: Cho tam giác ABC có đường cao AH, $\widehat{B}=60°, \widehat{C} =45°$ và cạnh BC = 6 cm. Chứng minh rằng AH = $3\left(3-\sqrt{3}\right)$ cm.

    Lời giải:

    

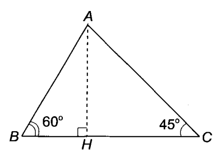
    Xét tam giác ABH vuông tại H ta có:

    $AH=BH.\tan B=BH.\tan 60°=BH\sqrt{3}$ hay $BH=\frac{AH}{\sqrt{3}}$

    Xét tam giác ACH vuông cân tại H nên AH = CH.

    Ta có BC = BH + CH hay 6 = $\frac{AH}{\sqrt{3}}+AH$$=AH.\left(\frac{1}{\sqrt{3}}+1\right)$

    Do đó $AH=\frac{6}{\frac{1}{\sqrt{3}}+1}=3\left(3-\sqrt{3}\right)$ (cm) (đpcm).

  • Bài 4.33 trang 52 sách bài tập Toán 9 Tập 1: Tính khoảng cách giữa hai địa điểm A, B ở hai bên hồ nước (không đo trực tiếp được), biết khoảng cách từ một địa điểm C đến A và đến B là CA = 90 m, CB = 150 m,$\widehat{CAB}$ = 120° (làm tròn đến m) (H.4.18).

    

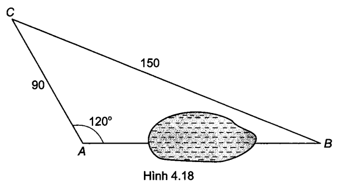
    Lời giải:

    

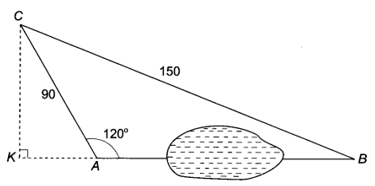
    Kẻ đường cao CK của tam giác ABC.

    $\widehat{CAK}=180°-\widehat{BAC}=180°-120°=60°$

    Xét tam giác CAK vuông tại K ta có:

    $AK=AC.\cos \widehat{CAK}=AC.\cos 60°=90.\cos 60°=45$ (m)

    $CK=AC.\sin \widehat{CAK}=90.\sin 60°=45\sqrt{3}$ (m)

    Áp dụng định lý Pythagore với tam giác BCK vuông tại K, ta có:

    $BK=\sqrt{B{C}^2-C{K}^2}=\sqrt{{150}^2-{\left(45\sqrt{3}\right)}^2}=15\sqrt{73}$ (m)

    Vậy AB = BK – AK = $15\sqrt{73}-45\approx 83$(m).

  • Bài 4.34 trang 52 sách bài tập Toán 9 Tập 1: Một cầu thủ đứng cách khung thành 18 m, đá quả bóng sát mặt đất, nghiêng một góc 20° so với phương vuông góc với khung thành, tới điểm M của khung thành (H.4.19). Tính khoảng cách từ cầu thủ đến điểm M (làm tròn đến dm).

    

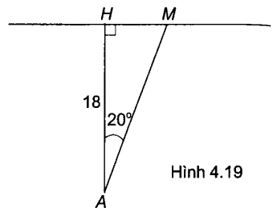
    Lời giải:

    Xét tam giác AHM vuông tại H ta có:

    (m) = 192 dm.

    Vậy khoảng cách từ cầu thủ đến điểm M xấp xỉ bằng 192 dm.

  • Bài 4.35 trang 52 sách bài tập Toán 9 Tập 1: Hai chiếc thuyền A và B ở vị trí được minh hoạ như trong Hình 4.20. Tính khoảng cách giữa chúng (làm tròn đến m), biết IK = 380 m.

    

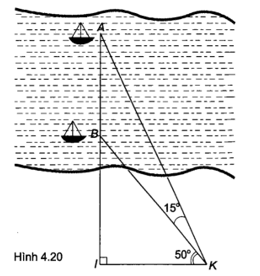
    Lời giải:

    Xét tam giác AIK vuông tại I ta có:

    $IA=IK.\tan \widehat{AKI}=380.\tan 65°$

    Xét tam giác IBK vuông tại I ta có:

    $IB=IK.\tan \widehat{IKB}=380.\tan 50°$

    Mà AB = IA – IB nên AB = 380 . tan 65° – 380 . tan 50° ≈ 362 (m).

    Vậy khoảng cách giữa hai chiếc thuyền xấp xỉ bằng 362 m.

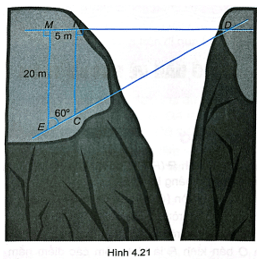
  • Bài 4.36 trang 52 sách bài tập Toán 9 Tập 1: Tìm độ dài dây cáp mắc giữa hai cọc ở vị trí C, D trên hai bên bờ vực như trong Hình 4.21 (làm tròn đến mét)

    

    Lời giải:

    Áp dụng kết quả bài 4.23 với p = 20 m, n = 5 m, α = 60° ta có:

    $CD=\frac{p\tan \alpha -n}{\sin \alpha }=\frac{20.\tan 60°-5}{\sin 60°}=\frac{20\sqrt{3}-5}{\frac{\sqrt{3}}{2}}\approx 34$ (m).

    Vậy độ dài dây cáp mắc giữa hai cọc C và D xấp xỉ bằng 34 m.

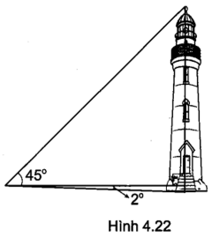
Bài 4.37 trang 52 sách bài tập Toán 9 Tập 1: Một người đứng cách chân ngọn hải đăng 50 m, nhìn xuống chân hải đăng dưới góc 2° và nhìn lên đỉnh ngọn hải đăng dưới góc 45° (so với đường nằm ngang) (H.4.22). Tính chiều cao ngọn hải đăng (làm tròn đến mét).

Lời giải:

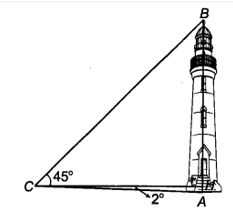
Gọi vị trí chân hải đăng là A, đỉnh hải đăng là B, đầu người quan sát là C, H là hình chiều vuông góc của C lên AB.

Theo đề bài, ta có: CH = 50 m, $\widehat{CAH}=2°, \widehat{HCB}=45°$

Xét tam giác HAC vuông tại H ta có:

$AH=CH.\tan \widehat{HCA}=50\tan 2°$

Tam giác HCB vuông tại H, $\widehat{HCB}=45°$ nên tam giác HCB vuông cân tại H, suy ra HB = HC = 50 m.

AB = AH + HB = 50 . tan 2° + 50° ≈ 52 (m).

Vậy chiều cao ngọn hải đăng xấp xỉ bằng 52 m.