Sách bài tập Toán 9 Bài 16 (Kết nối tri thức): Vị trí tương đối của đường thẳng và đường tròn

Giải SBT Toán 9 Bài 16: Vị trí tương đối của đường thẳng và đường tròn

Bài 5.17 trang 65 sách bài tập Toán 9 Tập 1: Cho đường tròn (O) và điểm P.

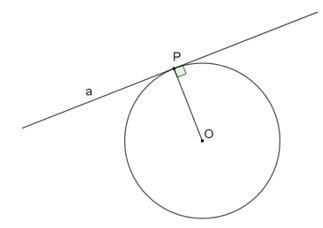
a) Giả sử $P\in \left(O\right)$. Vẽ đường thẳng a đi qua P và vuông góc với OP. Chứng minh rằng a là tiếp tuyến của đường tròn (O) tại P.

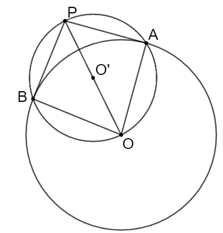
b) Giả sử P nằm ngoài (O). Vẽ đường tròn đường kính OP. Đường tròn vừa vẽ cắt (O) tại A và B. Chứng minh rằng PA và PB là hai tiếp tuyến của (O).

Lời giải:

a)

Ta có OP là bán kính đường tròn (O) (do $P\in \left(O\right)$) và a ⊥ OP.

Do đó a là tiếp tuyến của đường tròn (O) tại P. (đpcm)

b)

Gọi đường tròn bán kính OP là đường tròn (O').

Do A nằm trên đường tròn (O') đường kính OP nên tam giác BOP vuông tại B.

Suy ra OB ⊥ BP.

Ta có: OB là bán kính đường tròn (O) và OB ⊥ BP.

Do đó BP là tiếp tuyến của đường tròn (O) tại B. (đpcm)

Tương tự ta chứng minh được PA là tiếp tuyến của đường tròn (O) tại A.

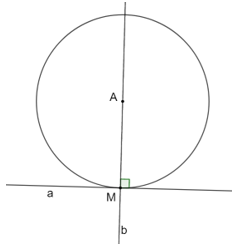
Bài 5.18 trang 65 sách bài tập Toán 9 Tập 1: Cho đường thẳng a, điểm M thuộc a và số dương R. Vẽ đường thẳng b đi qua M và vuông góc với a. Trên b xác định điểm A sao cho AM = R (đvđd). Chứng minh rằng đường tròn (A; R) tiếp xúc với a tại M. Ta có thể vẽ được mấy đường tròn như thế?

Lời giải:

Ta có: a ⊥ AM (do a ⊥ b và $M\in b$);

AM là bán kính của (A; R).

Do đó a là tiếp tuyến của (A; R) tại M hay (A; R) tiếp xúc với a tại M. (đpcm)

Có thể vẽ được hai đường tròn như thế, vì ta có thể lấy 2 điểm A nằm trên b nằm về hai phía của đường thẳng a và cách M một khoảng bằng R.

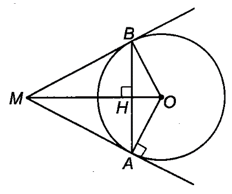
Bài 5.19 trang 65 sách bài tập Toán 9 Tập 1: Cho đường tròn (O) và điểm M nằm bên ngoài (O). Từ M kẻ tiếp tuyến MA với (O), trong đó A là tiếp điểm. Đường thẳng qua A và vuông góc với MO cắt (O) tại B (khác A).

a) Chứng minh rằng MB là tiếp tuyến của (O);

b) Tính OM và diện tích phần của tam giác AMB nằm bên ngoài (O), biết bán kính của (O) bằng 3 cm và $\widehat{MAB}$ = 60°.

Lời giải:

a) Gọi H là giao điểm của MO và AB.

+ Xét hai tam giác vuông AOH và BOH có:

Chung cạnh OH; OA = OB (bán kính đường tròn (O))

Do đó ∆AOH = ∆BOH (c.g.c), suy ra $\widehat{AOH}=\widehat{BOH}$, hay $\widehat{AOM}=\widehat{BOM}$.

+ Xét ∆AOM và ∆BOM có:

Chung cạnh OM; $\widehat{AOM}=\widehat{BOM}$; OA = OB

Do đó ∆AOM = ∆BOM (c.g.c), suy ra $\widehat{OBM}=\widehat{OAM}=90°$ hay OB ⊥ MB.

Ta có: OB ⊥ MB và OB là bán kính của đường tròn (O)

Do đó MB là tiếp tuyến của đường tròn (O). (đpcm)

b) Vì MA và MB là hai tiếp tuyến của đường tròn (O) và cắt nhau tại M nên MA = MB, suy ra tam giác MAB cân tại M. Mà $\widehat{MAB}=60°$ nên tam giác MAB là tam giác đều.

Xét tứ giác AOBM ta có: $\widehat{AOB}+\widehat{OBM}+\widehat{BMA}+\widehat{MAO}=360°$

Suy ra $AOB=360°-\widehat{OBM}-\widehat{BMA}-\widehat{MAO}$

$=360°-90°-60°-90°=120°$

Do đó số đo cung nhỏ AB là sđ $\stackrel{⏜}{AB}=120°$.

Diện tích hình quạt ứng với cung nhỏ AB là:

$S_q=\frac{120}{360}\pi R^2=\frac{120}{360}\pi {.3}^2=3\pi$ (cm²)

Ta có $\widehat{AOM}=\frac{1}{2}\widehat{AOB}=\frac{1}{2}.120°=60°$(tính chất hai tiếp tuyến cắt nhau)

Xét tam giác AOM vuông tại A, ta có:

$AM=AO.\tan \widehat{AOM}=3.\tan 60°=3\sqrt{3}$ (cm)

Theo câu a, ∆AOM = ∆BOM nên ta có:

$S_{AOBM}=2S_{AOM}=OA.AM=3.3\sqrt{3}=9\sqrt{3}$ (cm²)

Diện tích phần tam giác AMB nằm bên ngoài đường tròn (O) là:

$S_{AOBM}-S_q=9\sqrt{3}-3\pi$ (cm²)

Áp dụng định lý Pythagore với tam giác AOM ta được:

$OM=\sqrt{M{A}^2+O{A}^2}=\sqrt{{\left(3\sqrt{3}\right)}^2+3^2}=6$ (cm).

Vậy OM = 6 cm và diện tích phần tam giác AMB nằm bên ngoài đường tròn (O) là $9\sqrt{3}-3\pi$cm².

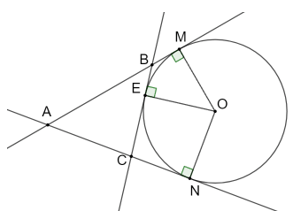
Bài 5.20 trang 65 sách bài tập Toán 9 Tập 1: Cho AM và AN là hai tiếp tuyến cắt nhau của đường tròn (O), trong đó M và N là hai tiếp điểm. Gọi E là một điểm thuộc cung nhỏ MN. Tiếp tuyến của (O) tại E cắt AM tại B và cắt AN tại C. Biết AB = 10 cm, AC = 7 cm và BC = 6 cm. Tính độ dài của các đoạn thẳng AM, AN, BM và CN.

Lời giải:

Do AM và AN, BM và BE, CN và CE là các cặp tiếp tuyến cắt nhau của (O) nên ta có:

AM = AN; BM = BE; CN = CE

Suy ra AM + AN = AB + BM + AC + CN = AB + BE + AC + CE

Do đó 2AM = AB + AC + (BE + CE) = AB + AC + BC

Khi đó $AM=\frac{AB+AC+BC}{2}=\frac{10+7+6}{2}=\mathrm{11,5}$(cm);

AN = AM = 11,5 cm;

BM = AM – AB = 11,5 – 10 = 1,5 (cm);

CN = AN – AC = 11,5 – 7 = 4,5 (cm).

Vậy AM = AN = 11,5 cm, BM = 1,5 cm và CN = 4,5 cm.

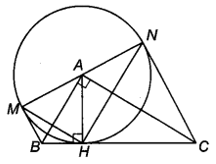
Bài 5.21 trang 65 sách bài tập Toán 9 Tập 1: Cho tam giác ABC vuông tại A, có đường cao AH.

a) Chứng minh rằng BC tiếp xúc với đường tròn (A) bán kính AH;

b) Gọi M và N là các điểm đối xứng với H lần lượt qua AB và AC. Chứng minh rằng BM và CN là hai tiếp tuyến của (A);

C) Chứng minh rằng MN là một đường kính của (A);

d) Tính diện tích của tứ giác BMNC, biết HB = 2 cm và HC = 4,5 cm.

Lời giải:

a) Ta thấy AH là bán kính của đường tròn (A) bán kính AH và AH ⊥ BC.

Do đó BC là tiếp tuyến của đường tròn (A) bán kính AH tại H. (đpcm)

b) Do M đối xứng với H qua B nên AM = AH, BM = BH.

Xét hai tam giác MAB và HAB có:

Chung cạnh AB; AM = AH; BM = BH.

Do đó ∆MAB = ∆HAB (c.c.c), suy ra $\widehat{AMB}=\widehat{AHB}=90°$ hay AM ⊥ MB.

Từ ∆MAB = ∆HAB (c.c.c), suy ra AM = AH.

Do đó M nằm trên đường tròn (A) bán kính AH.

Ta có: AM là bán kính của đường tròn (A) bán kính AH và AM ⊥ MB

Do đó MB là tiếp tuyến của đường tròn (A) bán kính AH tại M. (đpcm)

Tương tự ta chứng minh được CN là tiếp tuyến của đường tròn (A) bán kính AH tại N.

c) Theo câu b, ∆MAB = ∆HAB nên $\widehat{MAB}=\widehat{HAB}$

Tương tự, ∆NAC = ∆HAC nên $\widehat{NAC}=\widehat{HAC}$.

Mà $\widehat{HAB}+\widehat{HAC}=90°$ do tam giác ABC vuông tại A nên:

$\widehat{MAB}+\widehat{HAB}+\widehat{HAC}+\widehat{NAC}=2\left(\widehat{HAB}+\widehat{HAC}\right)=2.90°=180°$

Suy ra M, A, N thẳng hàng.

Mà M và N nằm trên (A) nên MN là đường kính của (A). (đpcm)

d) Theo câu b, BM ⊥ MN và CN ⊥ MN nên BM // CN, suy ra tứ giác BMNC là hình thang vuông.

M đối xứng với H qua AB nên BM = BH.

N đối xứng với H qua AC nên CN = CH.

Ta có BM + CN = BH + CH = 2 + 4,5 = 6,5 (cm)

Xét hai tam giác HBA và ABC ta có:

Chung góc B; $\widehat{BHA}=\widehat{BAC}=90°$

Suy ra ∆HBA ᔕ ∆ABC (g.g), do đó $\widehat{BAH}=\widehat{ACH}$

Xét hai tam giác HBA và HBC có:

$\widehat{BHA}=\widehat{CHA}=90°$

$\widehat{BAH}=\widehat{ACH}$

Suy ra ∆HBA ᔕ ∆HBC (g.g), do đó ta có:

$\frac{AH}{CH}=\frac{BH}{AH}$ hay $AH=\sqrt{BH.CH}=\sqrt{\mathrm{4,5.2}}=3$(cm)

MN là đường kính của (A) nên MN = 2AH = 2 . 3 = 6 (cm)

Diện tích tứ giác BMNC là:

$\frac{1}{2}MN\left(BM+CN\right)=\frac{1}{2}\mathrm{.6,5.6}=\mathrm{19,5}$ (cm²)

Vậy diện tích tứ giác BMNC là 19,5 cm².

Lý thuyết Vị trí tương đối của đường thẳng và đường tròn

1. Vị trí tương đối của đường thẳng và đường tròn

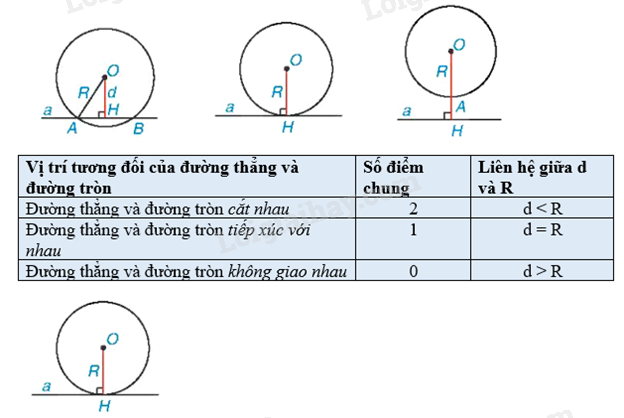
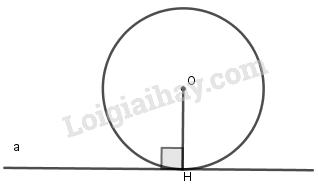
Điểm chung H của đường thẳng và đường tròn tiếp xúc với nhau goi là tiếp điểm. Khi đó đường thẳng a còn gọi là tiếp tuyến của đường tròn (O) tại H.

Đường thẳng a tiếp xúc với đường tròn (O) tại H thì $OH\mathrm{\perp }a$.

2. Dấu hiệu nhận biết tiếp tuyến của đường tròn

Dấu hiệu nhận biết tiếp tuyến

3. Hai tiếp tuyến cắt nhau của một đường tròn

Tính chất của hai tiếp tuyến cắt nhau

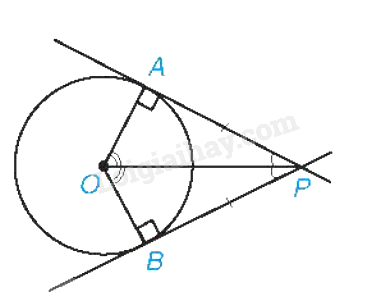
Ví dụ: Cho đường tròn (O), B, C $\in$ (O). Tiếp tuyến của (O) tại B và C cắt nhau tại A.

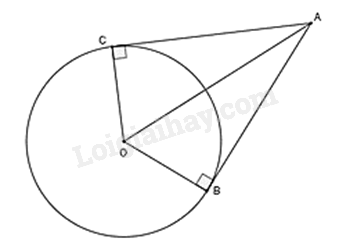
Khi đó:

- AB = AC

- Tia AO là tia phân giác của $\widehat{BAC}$.

- Tia OA là tia phân giác của $\widehat{BOC}$.