Sách bài tập Toán 9 (Kết nối tri thức) Bài tập cuối chương 1 trang 17

Giải SBT Toán 9 Bài tập cuối chương 1 trang 17

A. Trắc nghiệm

Bài 1 trang 17 sách bài tập Toán 9 Tập 1: Hệ phương trình nào sau đây là hệ hai phương trình bậc nhất hai ẩn?

A. $\left\{\begin{array}{c}2x+y=3\\ x-z=-1\end{array}\right.$.

B. $\left\{\begin{array}{c}2x+y=3\\ 0x+0y=1\end{array}\right.$.

C. $\left\{\begin{array}{c}2x+y=3\\ 0x-y=-1\end{array}\right.$.

D. $\left\{\begin{array}{c}2x+y=3\\ x+y^2=1\end{array}\right.$.

Lời giải:

Đáp án đúng là: C

Hệ phương trình A không là hệ hai phương trình bậc nhất hai ẩn vì hệ có 3 ẩn là x, y và z.

Hệ phương trình B không là hệ phương trình bậc nhất hai ẩn vì phương trình thứ hai có cả hai hệ số của hai ẩn x và y đều bằng 0.

Hệ phương trình C là hệ phương trình bậc nhất hai ẩn.

Hệ phương trình D không là hệ hai phương trình bậc nhất hai ẩn vì phương trình thứ hai có bậc 2 với ẩn y.

Bài 2 trang 17 sách bài tập Toán 9 Tập 1: Nghiệm của hệ phương trình $\left\{\begin{array}{c}4x+3y=-1\\ 2x-y=7\end{array}\right.$ là

A. (–1; 1).

B. (3; –1).

C. $\left(\frac{1}{2};-1\right)$.

D. (2; –3).

Lời giải:

Đáp án đúng là: D

Ta có $\left\{\begin{array}{c}4x+3y=-1\\ 2x-y=7\end{array}\right.$.

Nhân cả hai vế của phương trình thứ hai với 3 ta được:

$\left\{\begin{array}{c}4x+3y=-1\\ 6x-3y=21\end{array}\right.$.

Cộng từng vế của hai phương trình ta được:

10x = 20 hay $x=\frac{20}{10}=2$.

Thay vào phương trình thứ hai ta được:

2 . 2 – y = 7 hay y = 2 . 2 – 7 = –3.

Vậy hệ phương trình có nghiệm là (2; –3).

Bài 3 trang 18 sách bài tập Toán 9 Tập 1: Trong mặt phẳng toạ độ Oxy, cho các điểm M(1; 2), N(2; 3), P(–1; –1), Q(5; 8). Đường thẳng 3x – 2y = –1 đi qua hai điểm nào trong các điểm đã cho?

A. M và N.

B. M và P.

C. P và Q.

D. N và P.

Lời giải:

Đáp án đúng là: B và C

Ta thấy:

⦁ Thay tọa độ điểm M(1; 2) vào 3x – 2y = –1 , ta được 3 . 1 – 2 . 2 = –1.

Do đó, điểm M nằm trên đường thẳng d: 3x – 2y = –1.

⦁ Thay tọa độ điểm N(2; 3) vào 3x – 2y = –1 , ta được 3 . 2 – 2 . 3 = 0 ≠ –1.

Do đó, điểm N không nằm trên đường thẳng d: 3x – 2y = –1.

⦁ Thay tọa độ điểm P(–1; –1) vào 3x – 2y = –1 , ta được 3 . (­–1) – 2 . (–1) = –1.

Do đó, điểm P nằm trên đường thẳng d: 3x – 2y = –1.

⦁ Thay tọa độ điểm Q(5; 8) vào 3x – 2y = –1 , ta được 3 . 5 – 2 . 8 = –1.

Do đó, điểm Q nằm trên đường thẳng d: 3x – 2y = –1.

Vậy đường thẳng d: 3x – 2y = –1 đi qua ba điểm M, N, Q.

Bài 4 trang 18 sách bài tập Toán 9 Tập 1: Giá trị của a và b để đường thẳng y = ax + b đi qua hai điểm (1; –1) và (–1; 5) là

A. a = 1, b = –2.

B. a = –5, b = 1.

C. a = –3, b = 2.

D. a = –1, b = 0.

Lời giải:

Đáp án đúng là: C

Đường thẳng y = ax + b đi qua điểm (1; –1) nên ta có:

a . 1 + b = –1 hay a + b = –1

Đường thẳng y = ax + b đi qua điểm (–1; 5) nên ta có:

a . (–1) + b = 5 hay –a + b = 5

Ta được hệ phương trình: $\left\{\begin{array}{c}a+b=-1\\ -a+b=5\end{array}\right.$.

Cộng từng vế của hai phương trình ta được:

2b = 4 hay $b=\frac{4}{2}=2$.

Thay vào phương trình thứ nhất ta được:

a + 2 = –1 hay a = –1 – 2 = –3.

Vậy với a = –3 và b = 2 thì đường thẳng y = ax + b đi qua hai điểm (1; –1) và (–1; 5)

Bài 5 trang 18 sách bài tập Toán 9 Tập 1: Hệ phương trình nào sau đây có nghiệm duy nhất?

A. $\left\{\begin{array}{c}x-2y=3\\ 2x-4y=5\end{array}\right.$.

B. $\left\{\begin{array}{c}x-2y=3\\ -2x+4y=-6\end{array}\right.$.

C. $\left\{\begin{array}{c}x-2y=3\\ 2x+4y=5\end{array}\right.$.

D. $\left\{\begin{array}{c}x-2y=3\\ -x+2y=-2\end{array}\right.$.

Lời giải:

Đáp án đúng là: C

Sử dụng máy tính cầm tay ta được:

⦁ Hệ phương trình A vô nghiệm.

⦁ Hệ phương trình B có vô số nghiệm.

⦁ Hệ phương trình C có nghiệm duy nhất $\left(\frac{11}{4};-\frac{1}{8}\right)$.

⦁ Hệ phương trình D vô nghiệm.

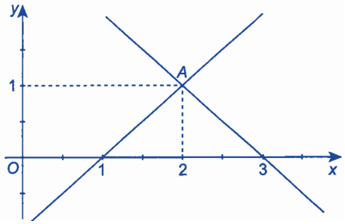
Bài 6 trang 18 sách bài tập Toán 9 Tập 1: Hình bên dưới minh hoạ tập nghiệm của hệ phương trình nào sau đây?

A. $\left\{\begin{array}{c}x-y=1\\ x-y=3\end{array}\right.$.

B. $\left\{\begin{array}{c}x-y=1\\ x+y=3\end{array}\right.$.

C. $\left\{\begin{array}{c}x+y=1\\ x-y=3\end{array}\right.$.

D. $\left\{\begin{array}{c}x+y=1\\ x+y=3\end{array}\right.$.

Lời giải:

Đáp án đúng là: B

Dễ thấy hai hệ phương trình $\left\{\begin{array}{c}x-y=1\\ x-y=3\end{array}\right.$ và $\left\{\begin{array}{c}x+y=1\\ x+y=3\end{array}\right.$ vô nghiệm vì trừ từng vế hai phương trình của hệ ta được 0x + 0y = 2.

⦁ Xét hệ phương trình $\left\{\begin{array}{c}x-y=1\\ x+y=3\end{array}\right.$:

Cộng từng vế hai phương trình ta được: 2x = 4 hay x = $\frac{4}{2}=2$.

Thay vào phương trình thứ nhất ta được: 2 – y = 1 hay y = 2 – 1 = 1.

Hệ có nghiệm là (2; 1).

⦁ Xét hệ phương trình $\left\{\begin{array}{c}x+y=1\\ x-y=3\end{array}\right.$:

Cộng từng vế hai phương trình ta được: 2x = 4 hay x = $\frac{4}{2}=2$.

Thay vào phương trình thứ nhất ta được: 2 + y = 1 hay y = 1 – 2 = –1.

Hệ có nghiệm là (2; –1).

Ta thấy giao điểm trên đồ thị có tọa độ là (2; 1). Vậy điểm này là minh họa cho tập nghiệm của hệ phương trình $\left\{\begin{array}{c}x-y=1\\ x+y=3\end{array}\right.$.

Bài 7 trang 18 sách bài tập Toán 9 Tập 1: Hệ phương trình $\left\{\begin{array}{c}3x-ay=b\\ ax+by=3\end{array}\right.$ có nghiệm là (2; –3) khi

A. a = 3, b = 3.

B. a = 3, b = –3.

C. a = –3, b = 3.

D. a = –3, b = –3.

Lời giải:

Đáp án đúng là: D

Hệ phương trình $\left\{\begin{array}{c}3x-ay=b\\ ax+by=3\end{array}\right.$ có nghiệm là (2; –3) nên ta có:

$\left\{\begin{array}{c}3.2-a.\left(-3\right)=b\\ a.2+b.\left(-3\right)=3\end{array}\right.$ hay $\left\{\begin{array}{c}6+3a=b\\ 2a-3b=3\end{array}\right.$, suy ra $\left\{\begin{array}{c}-3a+b=6\\ 2a-3b=3\end{array}\right.$.

Nhân cả hai vế của phương trình thứ nhất với 3, ta được:

$\left\{\begin{array}{c}-9a+3b=18\\ 2a-3b=3\end{array}\right.$

Cộng từng vế của hai phương trình ta được:

–7a = 21 hay $a=\frac{21}{-7}=-3$

Thay vào phương trình thứ nhất ta được:

(–3) . (­–3) + b = 6 hay 9 + b = 6, suy ra b = 6 – 9 = –3

Vậy với a = –3 và b = –3 thì hệ phương trình $\left\{\begin{array}{c}3x-ay=b\\ ax+by=3\end{array}\right.$ có nghiệm là (2; –3).

Bài 8 trang 18 sách bài tập Toán 9 Tập 1: Hệ phương trình $\left\{\begin{array}{c}x+my=1\\ -mx-y=-1\end{array}\right.$ có vô số nghiệm trong trường hợp nào sau đây?

A. m = 1.

B. m = –1.

C. m = 2.

D. m = –2.

Lời giải:

Đáp án đúng là: A

Cộng từng vế của hai phương trình ta được:

(1 – m)x + (m – 1)y = 0

Hệ phương trình có vô số nghiệm khi phương trình trên có dạng 0x + 0y = 0 hay 1 – m = 0 và m – 1 = 0, suy ra m = 1.

B. Tự luận

Bài 1.25 trang 19 sách bài tập Toán 9 Tập 1: Hai nghiệm của phương trình ax + by = 1 là (3; –1) và (–4; –2). Tìm a và b.

Lời giải:

(3; –1) là nghiệm của phương trình ax + by = 1 nên ta có:

a . 3 + b . (–1) = 1 hay 3a – b = 1

(–4; –2) là nghiệm của phương trình ax + by = 1 nên ta có:

a . (–4) + b . (–2) = 1 hay –4a – 2b = 1

Ta được hệ phương trình: $\left\{\begin{array}{c}3a-b=1\\ -4a-2b=1\end{array}\right.$.

Nhân hai vế của phương trình thứ nhất với 2 ta được: $\left\{\begin{array}{c}6a-2b=2\\ -4a-2b=1\end{array}\right.$.

Trừ từng vế của phương trình thứ nhất cho phương trình thứ hai ta được:

10a = 1 hay $a=\frac{1}{10}=0,1$.

Thay vào phương trình thứ nhất ta được:

3 . 0,1 – b = 1 hay 0,3 – b = 1, suy ra b = 0,3 – 1 = –0,7

Vậy với a = 0,1 và b = –0,7 thì hai nghiệm của phương trình ax + by = 1 là (3; –1) và (–4; –2).

Bài 1.26 trang 19 sách bài tập Toán 9 Tập 1: Giải các hệ phương trình sau:

a) $\left\{\begin{array}{c}0,4x+0,3y=1,1\\ -0,5x+0,2y=1,5\end{array}\right.$.

b) $\left\{\begin{array}{c}\frac{1}{3}x-\frac{1}{2}y=1\\ -4x+6y=3\end{array}\right.$.

c) $\left\{\begin{array}{c}0,2x-0,3y=0,6\\ -\frac{1}{3}x+\frac{1}{2}y=-1\end{array}\right.$.

Lời giải:

a) Nhân hai vế của phương trình thứ nhất với 5 và nhân hai vế của phương trình thứ hai với 4 ta được:

$\left\{\begin{array}{c}2x+1,5y=5,5\\ -2x+0,8y=6\end{array}\right.$.

Cộng từng vế hai phương trình ta được:

2,3y = 11,5 hay $y=\frac{11,5}{2,3}=5$.

Thay vào phương trình thứ nhất ta được:

2x + 1,5 . 5 = 5,5 hay 2x + 7,5 = 5,5, suy ra $x=\frac{5,5-7,5}{2}=-1$.

Vậy hệ phương trình có nghiệm là (–1; 5).

b) Nhân hai vế của phương trình thứ nhất với 12 ta được:

$\left\{\begin{array}{c}4x-6y=12\\ -4x+6y=3\end{array}\right.$.

Cộng từng vế hai phương trình ta được:

0x + 0y = 15 (vô nghiệm).

Vậy hệ phương trình không có nghiệm.

c) Nhân hai vế của phương trình thứ nhất với 10 và nhân hai vế của phương trình thứ hai với 6 ta được:

$\left\{\begin{array}{c}2x-3y=6\\ -2x+3y=-6\end{array}\right.$.

Cộng từng vế hai phương trình ta được:

0x + 0y = 0 (vô số nghiệm).

Xét phương trình 2x – 3y = 6, ta có $y=\frac{6+3x}{2}=3+\frac{3}{2}x$.

Vậy hệ phương trình có nghiệm $\left(x;3+\frac{3}{2}x\right)$ với $x\in ℝ$ tùy ý.

Bài 1.27 trang 19 sách bài tập Toán 9 Tập 1: Cho hệ phương trình $\left\{\begin{array}{c}mx+9y=m+3\\ x+my=2\end{array}\right.$.

Giải hệ phương trình đã cho trong mỗi trường hợp sau:

a) m = 1;

b) m = –3;

c) m = 3.

Lời giải:

a) Với m = 1 ta có hệ phương trình: $\left\{\begin{array}{c}x+9y=4\\ x+y=2\end{array}\right.$.

Trừ từng vế của phương trình thứ nhất cho phương trình thứ hai ta được:

8y = 2 hay $y=\frac{2}{8}=\frac{1}{4}$.

Thay vào phương trình thứ hai ta được:

$x+\frac{1}{4}=2$ hay $x=2-\frac{1}{4}=\frac{7}{4}$.

Vậy với m = 1 hệ có nghiệm là $\left(\frac{7}{4};\frac{1}{4}\right)$.

b) Với m = –3 ta có hệ phương trình: $\left\{\begin{array}{c}-3x+9y=0\\ x-3y=2\end{array}\right.$.

Nhân hai vế của phương trình thứ hai với 3 ta được:

$\left\{\begin{array}{c}-3x+9y=0\\ 3x-9y=6\end{array}\right.$.

Cộng từng vế của hai phương trình ta được: 0x + 0y = 6 (vô nghiệm).

Vậy với m = 1 hệ phương trình không có nghiệm.

c) Với m = 3 ta có hệ phương trình: $\left\{\begin{array}{c}3x+9y=6\\ x+3y=2\end{array}\right.$.

Nhân hai vế của phương trình thứ hai với 3 ta được:

$\left\{\begin{array}{c}3x+9y=6\\ 3x+9y=6\end{array}\right.$.

Trừ từng vế của phương trình thứ nhất cho phương trình thứ hai ta được:

0x + 0y = 0 (vô số nghiệm).

Xét phương trình x + 3y = 2, ta có $y=\frac{2-x}{3}=\frac{2}{3}-\frac{1}{3}x$.

Vậy với m = 3 hệ có nghiệm là $\left(x;\frac{2}{3}-\frac{1}{3}x\right)$ với $x\in ℝ$ tùy ý.

Bài 1.28 trang 19 sách bài tập Toán 9 Tập 1: Tìm a để ba đường thẳng sau đồng quy:

d₁: x – y = 1;

d₂: x + y = 3;

d₃: 2x + ay = 1.

Lời giải:

Tọa độ giao điểm của hai đường thẳng d₁ và d₂ là nghiệm của hệ phương trình:

$\left\{\begin{array}{c}x-y=1\\ x+y=3\end{array}\right.$.

Cộng hai vế của hai phương trình ta được:

2x = 4 hay $x=\frac{4}{2}=2$.

Thay vào phương trình thứ hai ta được:

2 + y = 3 hay y = 3 – 2 = 1.

Suy ra giao điểm của hai đường thẳng d₁ và d₂ là điểm có tọa độ (2; 1).

Để 3 đường thẳng trên đồng quy thì đường thẳng d₃ cũng phải đi qua điểm (2; 1).

Suy ra 2 . 2 + a . 1 = 1 hay 4 + a = 1, suy ra a = 1 – 4 = –3.

Vậy với a = –3 thì 3 đường thẳng đã cho đồng quy tại điểm có tọa độ (2; 1).

Bài 1.29 trang 19 sách bài tập Toán 9 Tập 1: Điểm mà tại đó chi phí sản xuất của công ty bằng doanh thu của nó được gọi là điểm hoà vốn. Dưới đây, C thể hiện chi phí sản xuất (tính bằng đô la) của x đơn vị sản phẩm và R thể hiện doanh thu (tính bằng đô la) từ việc bán x đơn vị sản phẩm. Tìm số lượng sản phẩm cần sản xuất và bán đề hoà vốn, nghĩa là tìm giá trị của x để C = R với $\left\{\begin{array}{c}C=15x+12 000\\ R=18x-6 000\end{array}\right.$

Tính doanh thu của công ty khi đó.

Lời giải:

Tại điểm hòa vốn ta có C = R nên hệ phương trình ở đề bài tương đương với:

$\left\{\begin{array}{c}R=15x+12 000\\ R=18x-6 000\end{array}\right.$ hay $\left\{\begin{array}{c}R-15x=12 000\\ R-18x=-6 000\end{array}\right.$.

Trừ từng vế của phương trình thứ nhất cho phương trình thứ hai ta được:

3x =18 000 hay $x=\frac{18 000}{3}=6 000$.

Thay vào phương trình thứ nhất ta được:

R – 15 . 6 000 = 12 000 hay R = 12 000 + 15 . 6 000 = 102 000.

Vậy doanh thu của công ty khi hòa vốn là 102 000 đô la.

Bài 1.30 trang 19 sách bài tập Toán 9 Tập 1: Một buổi biểu diễn ca nhạc bán được 1 500 vé. Mỗi vé loại I có giá 250 nghìn đồng và mỗi vé loại II có giá 150 nghìn đồng. Tổng số tiền bán vé thu được là 285 triệu đồng. Hỏi mỗi loại vé đã bán được bao nhiêu vé?

Lời giải:

Gọi x, y (vé) lần lượt là số vé loại I và số vé loại II đã bán ($x,y\in \mathbb{N}*$).

Tổng số vé đã bán là 1 500 vé nên ta có: x + y = 1 500.

Tổng số tiền bán vé là 285 triệu đồng nên ta có:

250 000x + 150 000y = 285 000 000 hay 25x + 15y = 28 500.

Ta được hệ phương trình: $\left\{\begin{array}{c}x+y=1 500\\ 25x+15y=28 500\end{array}\right.$.

Nhân cả hai vế của phương trình thứ nhất với 15 ta được:

$\left\{\begin{array}{c}15x+15y=22 500\\ 25x+15y=28 500\end{array}\right.$.

Trừ từng vế của phương trình thứ hai cho phương trình thứ nhất ta được:

10x = 6 000 hay $x=\frac{6 000}{10}=600$.

Thay vào phương trình thứ nhất ta được:

600 + y = 1 500 hay y = 1 500 – 600 = 900.

Vậy buổi biểu diễn đã bán được 600 vé loại I và 900 vé loại II.

Bài 1.31 trang 19 sách bài tập Toán 9 Tập 1: Một khẩu phần súp cà chua chứa 100 calo và 18 gam carbohydrate. Một lát bánh mì nguyên hạt chứa 70 calo và 13 gam carbohydrate, cần bao nhiêu khẩu phần mỗi loại để có được 230 calo và 42 gam carbohydrate?

Lời giải:

Gọi x, y lần lượt là số khẩu phần súp cá chua và lát bánh mì để đạt được 230 calo và 42 gam carbohydrate ($x,y\in \mathbb{N}*$).

Lượng calo cần đạt được là 230 calo nên ta có:

100x + 70y = 230 hay 10x + 7y = 23.

Lượng carbohydrate cần đạt được là 42 gam nên ta có:

18x + 13y = 42.

Ta được hệ phương trình: $\left\{\begin{array}{c}10x+7y=23\\ 18x+13y=42\end{array}\right.$.

Nhân hai vế của phương trình thứ nhất với 13 và nhân hai vế của phương trình thứ hai với 7 ta được:

$\left\{\begin{array}{c}130x+91y=299\\ 126x+91y=294\end{array}\right.$.

Trừ từng vế của phương trình thứ nhất cho phương trình thứ hai ta được:

4x = 5 hay $x=\frac{5}{4}$.

Thay vào phương trình thứ nhất ta được:

$10.\frac{5}{4}+7y=23$ hay $\frac{25}{2}+7y=23$, suy ra $y=\frac{3}{2}$.

Vậy cần $\frac{5}{4}$ khẩu phần súp cà chua và $\frac{3}{2}$ lát bánh mì để có 230 calo và 42 gam carbohydrate.

Bài 1.32 trang 19 sách bài tập Toán 9 Tập 1: Một loại xe ô tô có mức tiêu hao nhiên liệu là 8,1 lít/100 km khi lái xe trong thành phố và 4,8 lít/100 km khi lái xe trên đường cao tốc. Vào một ngày Chủ nhật, chiếc xe đi tổng quãng đường trong thành phố và trên đường cao tốc là 165 km và tiêu thụ hết 8,415 lít xăng. Tính độ dài quãng đường xe ô tô đi trong thành phố và trên đường cao tốc vào ngày Chủ nhật đó.

Lời giải:

Gọi x, y (km) lần lượt là quãng đường ô tô đã đi trong thành phố và trên đường cao tốc ($x,y\in \mathbb{N}*$).

Tổng quãng đường ô tô đã đi là: x + y = 165 (km).

Lượng xăng ô tô đã tiêu thụ hết là:

8,1x + 4,8y = 8,415 . 100 = 841,5 (lít).

Ta được hệ phương trình: $\left\{\begin{array}{c}x+y=165\\ 8,1x+4,8y=841,5\end{array}\right.$.

Nhân hai vế của phương trình thứ nhất với 4,8 ta được:

$\left\{\begin{array}{c}4,8x+4,8y=792\\ 8,1x+4,8y=841,5\end{array}\right.$.

Trừ từng vế của phương trình thứ hai cho phương trình thứ nhất ta được:

3,3x = 49,5 hay $x=\frac{49,5}{3,3}=15$.

Thay vào phương trình thứ nhất, ta được:

15 + y = 165 hay y = 165 – 15 = 150.

Vậy ô tô đã đi 15 km trong thành phố và 150 km trên đường cao tốc.

Tổng hợp lý thuyết Toán 9 Chương 1

1. Phương trình bậc nhất hai ẩn

Khái niệm phương trình bậc nhất hai ẩn: Phương trình bậc nhất hai ẩn x và y là hệ thức dạng ax + by = c (1), trong đó a, b và c là các số đã biết (a ≠ 0 hoặc b ≠ 0).

Khái niệm nghiệm của phương trình bậc nhất hai ẩn: Nếu tại x = x₀ và y = y₀ ta có ax₀ + by₀ = c là một khẳng định đúng thì cặp số (x₀; y₀) được gọi là một nghiệm của phương trình (1).

Chú ý: Một phương trình bậc nhất hai ẩn đều có vô số nghiệm.

Nhận xét: Trong mặt phẳng tọa độ, tập hợp các điểm có tọa độ (x; y) thỏa mãn phương trình bậc nhất hai ẩn ax + by = c là một đường thẳng. Đường thẳng đó gọi là đường thẳng ax + by = c.

2. Hệ hai phương trình bậc nhất hai ẩn

Khái niệm hệ hai phương trình bậc nhất hai ẩn: Một cặp gồm hai phương trình bậc nhất hai ẩn ax + by = c và a’x + b’y = c’ được gọi là một hệ hai phương trình bậc nhất hai ẩn. Ta thường viết hệ phương trình đó dưới dạng: $\left\{\begin{array}{l}ax+by=c\\ a^{\text{'}}x+b^{\text{'}}y=c^{\text{'}}.\end{array}\right.\left(*\right)$

Khái niệm nghiệm của hệ hai phương trình bậc nhất hai ẩn: Mỗi cặp số (x₀; y₀) được gọi là một nghiệm của hệ (*) nếu nó đồng thời là nghiệm của cả hai phương trình của hệ (*).

Lưu ý: Mỗi nghiệm của hệ (*) chính là một nghiệm chung của hai phương trình của hệ (*).

Chú ý: Cặp số (x₀; y₀) là nghiệm của hệ phương trình (*) có nghĩa là điểm có tọa độ (x₀; y₀) vừa thuộc đường thẳng ax + by = c, vừa thuộc đường thẳng a’x + b’y = c’. Vậy điểm có tọa độ (x₀; y₀) là giao điểm của hai đường thẳng ax + by = c và a’x + b’y = c’.

3. Phương pháp thế

Cách giải hệ phương trình bằng phương pháp thế:

Bước 1. Từ một phương trình của hệ, biểu diễn một ẩn theo ẩn kia rồi thế vào phương trình còn lại của hệ để được phương trình chỉ còn chứa một ẩn.

Bước 2. Giải phương trình một ẩn vừa nhận được, từ đó suy ra nghiệm của hệ phương trình đã cho.

4. Phương pháp cộng đại số

Cách giải hệ phương trình bằng phương pháp cộng đại số:

Để giải một hệ hai phương trình bậc nhất hai ẩn có hệ số của cùng một ẩn nào đó trong hai phương trình bằng nhau hoặc đối nhau, ta có thể làm như sau:

Bước 1. Cộng hay trừ từng vế của hai phương trình trong hệ để được phương trình chỉ còn chứa một ẩn.

Bước 2. Giải phương trình một ẩn vừa nhận được, từ đó suy ra nghiệm của hệ phương trình đã cho.

Chú ý: Trường hợp trong hệ phương trình đã cho không có hai hệ số của cùng một ẩn bằng nhau hay đối nhau, ta có thể đưa về trường hợp đã xét bằng cách nhân hai về của mỗi phương trình với một số thích hợp (khác 0).

5. Sử dụng máy tính cầm tay để tìm nghiệm của hệ hai phương trình bậc nhất hai ẩn

Cách tìm nghiệm của hệ hai phương trình bậc nhất hai ẩn bằng máy tính cầm tay

Muốn tìm nghiệm của hệ hai phương trình bậc nhất hai ẩn bằng máy tính cầm tay (MTCT), chúng ta cần sử dụng loại máy có chức năng này (thường có phím MODE). Trước hết ta phải viết hệ phương trình cần tìm nghiệm dưới dạng: $\left\{\begin{array}{l}{a}_{1}x+b_{1}y=c_1\\ a_{2}x+b_{2}y=c_2.\end{array}\right.$

Chẳng hạn, để tìm nghiệm của hệ $\left\{\begin{array}{l}2x-3y-4=0\\ 5x-6y-7=0\end{array}\right.,$ ta viết nó dưới dạng $\left\{\begin{array}{l}2x-3y=4\\ 5x-6y=7\end{array}\right..$

Khi đó, ta có a₁ = 2, b₁ = 3, c₁ = 4; a₂ = 5, b₂ = 6 và c₂ = 7. Lần lượt thực hiện các bước sau (với máy tính thích hợp):

Bước 1. Vào chức năng giải hệ hai phương trình bậc nhất hai ẩn bằng cách bấm các phím (xem màn hình sau bước 1, con trỏ ở vị trí a₁).

Bước 2. Nhập các số a₁ = 2, b₁ = 3, c₁ = 4; a₂ = 5, b₂ = 6 và c₂ = 7 bằng cách bấm: (xem màn hình sau bước 2).

Bước 3. Đọc kết quả: Sau khi kết thúc bước 2, bấm màn hình cho x = –1; bấm tiếp phím màn hình cho y = 2 (xem màn hình sau bước 3). Ta hiểu nghiệm của hệ phương trình là (–1; 2).

Chú ý:

– Muốn xóa số vừa nhập thì bấm phím muốn thay đổi số đã nhập ở một vị trí nào đó thì di chuyển con trỏ đến vị trí đó rồi nhập số mới.

– Bấm phím hay để chuyển đổi hiển thị các giá trị của x và y trong kết quả.

– Nếu máy báo “Infinite Sol” thì hệ phương trình đã cho có vô số nghiệm. Nếu máy báo “No-Solution” thì hệ phương trình đã cho vô nghiệm.

6. Giải bài toán bằng cách lập hệ phương trình

Các bước giải một bài toán bằng cách lập hệ phương trình:

Bước 1. Lập hệ phương trình:

– Chọn ẩn số (thường chọn hai ẩn số) và đặt điều kiện thích hợp cho các ẩn số;

– Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết;

Bước 2. Giải hệ phương trình.

Bước 3. Trả lời: Kiểm tra xem trong các nghiệm tìm được của hệ phương trình, nghiệm nào thỏa mãn, nghiệm nào không thỏa mãn điều kiện của ẩn, rồi kết luận.