Sách bài tập Toán 9 Bài 12 (Kết nối tri thức): Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng
Với giải sách bài tập Toán 9 Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 9 Bài 12.
Giải SBT Toán 9 Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng
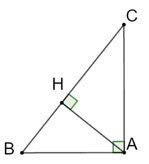
Bài 4.18 trang 49 sách bài tập Toán 9 Tập 1: Cho tam giác ABC vuông tại A với đường cao AH. Hãy tính cos C theo hai cách và suy ra AC2 = BC . HC.
Lời giải:
Xét tam giác ABC vuông tại A ta có: cosC=ACBC
Xét tam giác HAC vuông tại H ta có: cosC=HCAC
Suy ra ACBC=HCAC, hay AC2 = BC . HC (đpcm).
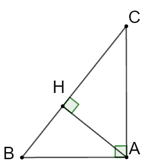
Bài 4.19 trang 49 sách bài tập Toán 9 Tập 1: Gọi AH là đường cao của tam giác ABC vuông tại A. Tính tan^ABH và tan^CAH, suy ra AH2 = BH . CH.
Lời giải:
Xét tam giác vuông ABH có tan^ABH=AHBH.
Xét tam giác vuông CAH có tan^ACH=AHCH.
Vì hai góc BAH và CAH là hai góc phụ nhau (tam giác ABC vuông tại A) nên ta có:
tan^ABH=cot^ACH=1tan^ACH , hay AHBH=CHAH
Suy ra AH2 = BH . CH (đpcm)
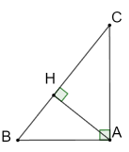
Bài 4.20 trang 49 sách bài tập Toán 9 Tập 1: Cho tam giác ABC vuông tại A, AH là đường cao. Chứng minh rằng 1AH2=1AB2+1AC2
(HD. Ta có sin B = AHAB, sin C = AHAC, cos B = sin C và áp dụng công thức sin2 α + cos2 α = 1 với mọi góc nhọn α).
Lời giải:
Xét tam giác ABH vuông tại H, ta có: tan^ABH=AHBH
Xét tam giác ACH vuông tại H ta có: tan^ACH=AHHC
Vì ^ABH và ^ACH là hai góc phụ nhau (tam giác ABC vuông tại A) nên:
tan^ABH=cot^ACH=1tan^ACH hay AHBH=HCAH
Suy ra AH2 = BH . CH (đpcm).
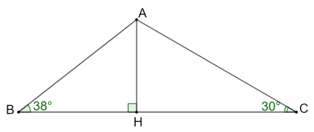
Bài 4.21 trang 49 sách bài tập Toán 9 Tập 1: Cho tam giác ABC có BC = 11 cm, ^ABC=38°, ^ACB=30°. Gọi H là chân của đường vuông góc kẻ từ A đến BC. Hãy tính AH.
Lời giải:
Vì hai góc B và C của tam giác ABC đều nhọn nên đường cao AH có chân đường cao H nằm giữa B và C.
Gọi h (cm) là độ dài đường cao AH của tam giác ABC.
Xét tam giác ABH vuông tại H, ta có:
tan^ABH=AHBH hay tan38°=hBH, suy ra BH=htan38°
Xét tam giác ACH vuông tại H, ta có:
tan^ACH=AHCH hay tan30°=hCH, suy ra CH=htan30°
Ta có: BC=BH+CH
Hay 11=htan38°+htan30°=h(1tan38°+1tan30°)
Do đó h=111tan38°+1tan30°≈3,652(cm).
Vậy AH ≈ 3,652 cm.
Bài 4.22 trang 49 sách bài tập Toán 9 Tập 1: Giải tam giác ABC vuông tại A, với AB = c, BC = a, CA = b trong các trường hợp (cạnh làm tròn đến chữ số thập phân thứ ba):
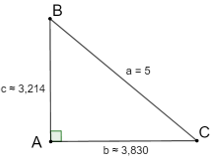
a) a = 5, ˆB = 50°;
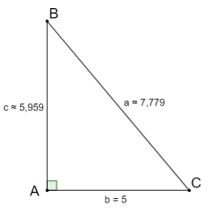
b) b = 5, ˆB = 40°;
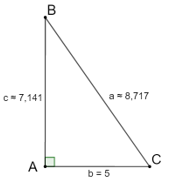
c) b = 5, ˆC = 55°
Lời giải:
a) Ta có: ˆC=90°−ˆB=90°−50°=40°
b=a.sinB=5.sin50°≈3,830
c=a.sinC=5.sin40°≈3,214
Vậy tam giác ABC có a = 5, b ≈ 3,830, c ≈ 3,214, ˆA=90°,ˆB=50°,ˆC=40°
b) Ta có: ˆC=90°−ˆB=90°−40°=50°
a=bsinB=5sin40°≈7,779
c=b.cot40°=5.cot40°≈5,959
c) Ta có: ˆB=90°−ˆC=90°−55°=35°
a=bcosC=5cos55°≈8,717
c=b.tanC=5.tan55°≈7,141
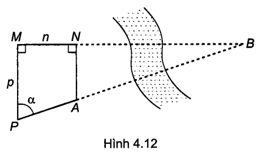
Bài 4.23 trang 49 sách bài tập Toán 9 Tập 1: Cho A, B là hai địa điểm ở hai bên bờ sông, biết AN và PM cùng vuông góc MN, MN = n (mét), MP = p (mét), p > n và ^MPA=α (H.4.12). Chứng minh rằng: AB=ptanα−nsinα.
Lời giải:
Vì AN và PM cùng vuông góc với MN nên AN // PM.
Vì AN // PM nên ^BAN=^BPM=α
+ Xét tam giác BAN vuông tại N ta có:
BN=ABsin^BAN=AB.sinα
+ Xét tam giác BPM vuông tại M ta có:
BM=PM.tan^BPM=p.tanα
Ta có: BM – BN = MN
p . tan α – AB . sinα = n
AB . sinα = p . tanα – n
AB=p.tanα−nsinα (đpcm).
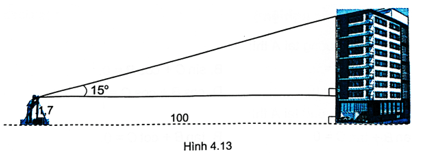
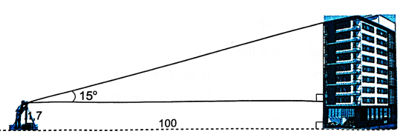
Bài 4.24 trang 49 sách bài tập Toán 9 Tập 1: Một người đứng xa toà nhà 100 m, dùng giác kế thẳng đứng ngắm thấy điểm trên nóc nhà với góc nhìn 15° (so với phương nằm ngang) (H.4.13). Hỏi toà nhà cao bao nhiêu mét (làm tròn đến chữ số thập phân thứ nhất), biết chiều cao của giác kế là 1,7 m?
Lời giải:
Gọi C là chân tòa nhà, D là điểm trên nóc tòa nhà, A là điểm đặt mắt giác kế.
Kẻ đường cao AH của tam giác ACD, ta có:
CH = 1,7 m, AH = 100 m, ^DAH=15°
Xét tam giác AHD vuông tại H, ta có:
HD=AH.tan^DAH=100.tan15°
Do đó CD = CH + HD = 1,7 + 100 . tan 15° ≈ 28,5 (m)
Vậy tòa nhà cao xấp xỉ 28,5 m.
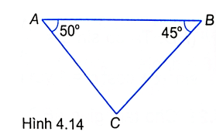
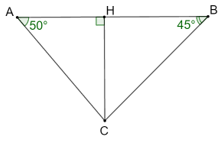
Bài 4.25 trang 50 sách bài tập Toán 9 Tập 1: Hai trạm quan trắc tàu biển đặt ở hai mỏm núi A và B cách nhau 2 km, nhìn thấy chiếc tàu C ở phía xa với với ^CAB=50°, ^CBA=45°(H.4.14). Hỏi tàu còn cách đường thẳng AB bao nhiêu mét?
Lời giải:
Kẻ đường cao CH vuông góc với AB.
+ Xét tam giác ACH vuông tại H ta có:
AH=CH.cotA=CH.cot50°
+ Xét tam giác BCH vuông tại H, ta có:
BH=CH.cotB=CH.cot45°
Do AB = AH + HB, nên
2000=CH.cot50°+CH.cot45°=CH(cot50°+cot45°)
Suy ra CH=2 000cot50°+cot45°≈1 087(m).
Vậy tàu còn cách đường thẳng AB xấp xỉ 1 087 m.
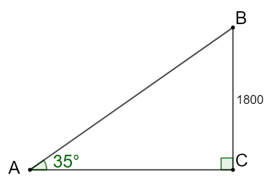
Bài 4.26 trang 50 sách bài tập Toán 9 Tập 1: Trong một trận chiến đấu, một máy bay của đối phương bay ở độ cao 1 800 m. Khẩu pháo cao xạ ngắm chiếc máy bay đó dưới một góc 35° so với phương nằm ngang. Tìm khoảng cách từ pháo cao xạ đến máy bay (làm tròn đến mét).
Lời giải:
Gọi vị trí của khẩu pháo cao xạ là A, vị trí máy bay là B, C là vị trí hình chiếu của máy bay với mặt đất.
Khi đó ta có: BC = 1 800 m, ^BAC=35°, khoảng cách từ pháo cao xạ tới máy bay là độ dài đoạn AB.
Xét tam giác ABC vuông tại C ta có:
AB=BCsinA=1 800sin35°≈3 138 (m).
Vậy khoảng cách từ pháo cao xạ tới máy bay xấp xỉ bằng 3 138 m.
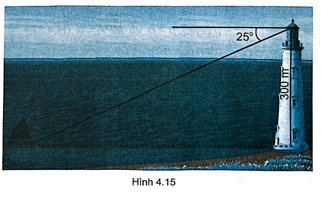
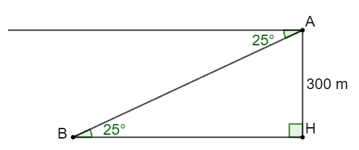
Bài 4.27 trang 50 sách bài tập Toán 9 Tập 1: Từ một đài quan sát ở cạnh bờ biển, có độ cao 300 m so với mặt biển, nhìn thấy một con tàu dưới một góc 25° (so với phương nằm ngang của mực nước biển). Hỏi khoảng cách từ tàu đến đài quan sát xấp xỉ bao nhiêu mét?
Lời giải:
Gọi vị trí đài quan sát là A, vị trí chân đài quan sát là H, vị trí con tàu là B.
Khi đó ta có: AH = 300 m, ^ABH=25°, khoảng cách từ tàu đến chân đài quan sát là đoạn BH.
Xét tam giác ABH vuông tại H, ta có:
BH=AH.cot^ABH=300.cot25°≈643 (m).
Vậy khoảng cách từ tàu đến chân đài quan sát xấp xỉ 643 m.
Lý thuyết Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng
1. Hệ thức giữa cạnh huyền và cạnh góc vuông
Công thức tính cạnh góc vuông theo cạnh huyền và sin, côsin của các góc nhọn
|
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề. Cạnh góc vuông = (cạnh huyền ) × (sin góc đối) = (cạnh huyền ) × (cosin góc kề) |
Ví dụ 1:
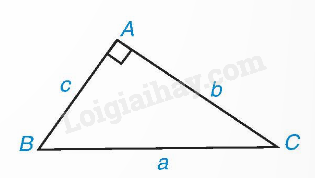
Trong tam giác ABC vuông tại A, ta có:
b=a.sinB=a.cosC;c=a.sinC=a.cosB.
2. Hệ thức giữa hai cạnh góc vuông
Công thức tính cạnh góc vuông theo cạnh góc vuông kia và tang, côtang của các góc nhọn
|
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tang góc đối hoặc côtang góc kề. Cạnh góc vuông = (cạnh góc vuông còn lại ) × (tan góc đối) = (cạnh góc vuông còn lại ) × (cot góc kề) |
Ví dụ 2:
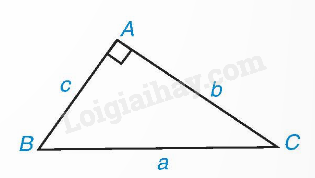
Trong tam giác ABC vuông tại A, ta có:
b=c.tanB=c.cotC;c=b.tanC=b.cotB.
3. Giải tam giác vuông
Bài toán Giải tam giác vuông
Trong một tam giác vuông, nếu cho biết trước hai cạnh (hoặc một góc nhọn và một cạnh) thì ta sẽ tìm được tất cả các cạnh và các góc còn lại của tam giác vuông đó.
Xem thêm các chương trình khác:
- Soạn văn 9 Kết nối tri thức (hay nhất)
- Văn mẫu 9 - Kết nối tri thức
- Tóm tắt tác phẩm Ngữ văn 9 – Kết nối tri thức
- Tác giả tác phẩm Ngữ văn 9 - Kết nối tri thức
- Bố cục tác phẩm Ngữ văn 9 – Kết nối tri thức
- Nội dung chính tác phẩm Ngữ văn 9 – Kết nối tri thức
- Soạn văn 9 Kết nối tri thức (ngắn nhất)
- Bài tập Tiếng Anh 9 Global success theo Unit có đáp án
- Giải sgk Tiếng Anh 9 - Global success
- Trọn bộ Từ vựng Tiếng Anh 9 Global success đầy đủ nhất
- Trọn bộ Ngữ pháp Tiếng Anh 9 Global success đầy đủ nhất
- Giải sbt Tiếng Anh 9 – Global Success
- Giải sgk Khoa học tự nhiên 9 – Kết nối tri thức
- Lý thuyết Khoa học tự nhiên 9 – Kết nối tri thức
- Giải sbt Khoa học tự nhiên 9 – Kết nối tri thức
- Giải sgk Lịch sử 9 – Kết nối tri thức
- Giải sbt Lịch sử 9 – Kết nối tri thức
- Giải sgk Địa lí 9 – Kết nối tri thức
- Giải sbt Địa lí 9 – Kết nối tri thức
- Giải sgk Tin học 9 – Kết nối tri thức
- Giải sbt Tin học 9 – Kết nối tri thức
- Giải sgk Công nghệ 9 – Kết nối tri thức
- Giải sgk Giáo dục công dân 9 – Kết nối tri thức
- Giải sbt Giáo dục công dân 9 – Kết nối tri thức
- Giải sgk Hoạt động trải nghiệm 9 – Kết nối tri thức