Sách bài tập Toán 9 Bài 14 (Kết nối tri thức): Cung và dây của một đường tròn
Với giải sách bài tập Toán 9 Bài 14: Cung và dây của một đường tròn sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 9 Bài 14.
Giải SBT Toán 9 Bài 14: Cung và dây của một đường tròn
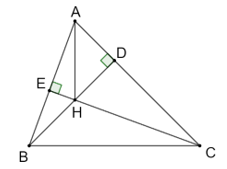
Bài 5.6 trang 59 sách bài tập Toán 9 Tập 1: Cho tam giác nhọn ABC, hai đường cao BD và CE cắt nhau tại H. Chứng minh rằng:
a) Bốn điểm A, E, H, D cùng thuộc một đường tròn.
b) AH > DE.
Lời giải:
a) Tam giác AEH vuông tại E nên 3 điểm A, E, H cùng nằm trên đường tròn đường kính AH.
Tam giác ADH vuông tại D nên 3 điểm A, D, H cùng nằm trên đường tròn đường kính AH.
Vậy 4 điểm A, E, H, D cùng nằm trên đường tròn đường kính AH.
b) Do góc A là góc nhọn nên dây DE của đường tròn đường kính AH không đi qua tâm của đường tròn (không phải đường kính).
Mà AH là đường kính của đường tròn đang xét nên AH < DE. (đpcm)
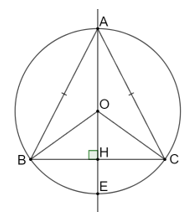
Bài 5.7 trang 59 sách bài tập Toán 9 Tập 1: Cho tam giác cân ABC (AB = AC). Gọi (O) là đường tròn đi qua ba điểm A, B, C và E là điểm trên cung nhỏ BC sao cho BE = EC.
a) Chứng minh rằng ba điểm A, O, E thẳng hàng.
b) Gọi H là chân đường cao hạ từ A xuống BC. Chứng minh rằng AH < AB < AE.
Lời giải:
a) Xét ∆OAB và ∆OAC có:
OB = OC (bán kính đường tròn (O))
AC = AC (theo đề bài)
Chung cạnh OA
Nên ∆OAB = ∆OAC (c.c.c), do đó
suy ra hay . (1)
Theo đề bài ta có , suy ra . (2)
Từ (1) và (2) suy ra sđ hay .
Mà nên
Suy ra cung ABE là nửa đường tròn.
Vậy 3 điểm A, O, E thẳng hàng. (đpcm)
b) Tam giác AHB vuông tại H nên AB là cạnh huyền của tam giác, AH là cạnh góc vuông nên AH < AB.
A, O, E thẳng hàng nên AE là đường kính của đường tròn (O), AB là một dây cung không đi qua tâm của đường tròn nên AB < AE.
Vậy AH < AB < AE. (đpcm)
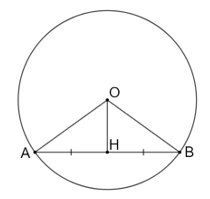
Bài 5.8 trang 59 sách bài tập Toán 9 Tập 1: Gọi H là trung điểm của dây AB không đi qua tâm của đường tròn (O).
a) Chứng minh rằng OH ⊥ AB.
b) Tính khoảng cách từ O đến AB, biết rằng AB = 8 cm và bán kính của (O) bằng 5 cm.
Lời giải:
a) Vì OA = OB (bán kính đường tròn (O)) nên ∆OAB cân tại O.
H là trung điểm của AB nên OH là đường trung tuyến đồng thời là đường cao của tam giác cân OAB.
Vây OH ⊥ AB. (đpcm)
b) H là trung điểm của AB nên (cm).
Áp dụng định lý Pythagore với tam giác OAH ta có:
(cm).
Vậy khoảng cách từ O đến AB là 3 cm.
Bài 5.9 trang 59 sách bài tập Toán 9 Tập 1: Kim giờ và kim phút của một chiếc đồng hồ tạo thành góc ở tâm có số đo là bao nhiêu độ vào mỗi thời điểm sau:
a) 3 giờ?
b) 6 giờ?
c) 8 giờ?
d) 11 giờ?
Lời giải:
Một chiếc đồng hồ có 12 số chỉ giờ.
Mỗi giờ, kim phút luôn đứng ở vị trí số 12, kim giờ di chuyển được vòng, ứng với cung
Với các thời điểm từ 7 đến 11 giờ, số đo góc ở tâm sẽ được tính là góc nhọn bằng 360° trừ đi số đo cung mà kim giờ đã di chuyển.
Vậy số đo góc ở tâm tương ứng với các thời điểm tương ứng là:
a) 3 . 30° = 90°.
b) 6 . 30° = 180°.
c) 360° – 8 . 30° = 120°.
d) 360° – 11 . 30° = 30°.
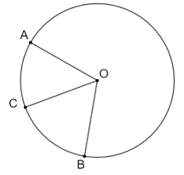
Bài 5.10 trang 59 sách bài tập Toán 9 Tập 1: Cho ba điểm A, B và c nằm trên đường tròn (O) sao cho và sđ . Tính số đo của cung lớn BC.
Lời giải:
Trường hợp 1: Điểm O nằm trong cung nhỏ AB:
Ta có
Do đó số đo cung nhỏ BC là 60°.
Vậy số đo cung lớn BC là 360° – 60° = 300°.
Trường hợp 2: Điểm O nằm trong cung lớn AB:
Do đó số đo cung nhỏ BC là 160°.
Vậy số đo cung lớn BC là 360° – 160° = 200°.
Lý thuyết Cung và dây của một đường tròn
1. Dây và đường kính của đường tròn
Khái niệm dây
Đoạn thẳng nối hai điểm tùy ý của một đường tròn gọi là một dây (hay dây cung) của đường tròn.
Khái niệm đường kính của đường tròn
Mỗi dây đi qua tâm là một đường kính của đường tròn.
Đường kính của đường tròn bán kính R là 2R.
Ví dụ:
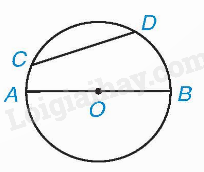
Trong hình trên, CD là một dây, AB là một đường kính của (O).
Quan hệ giữa dây và đường kính
|
Trong một đường tròn, đường kính là dây cung lớn nhất. |
2. Góc ở tâm, cung và số đo của một cung
Khái niệm góc ở tâm và cung tròn
|
Góc ở tâm là góc có đỉnh trùng với tâm của đường tròn. |
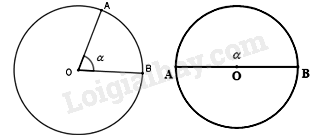
- Nếu thì cung nằm bên trong góc được gọi là cung nhỏ, cung nằm bên ngoài góc được gọi là cung lớn.
- Nếu thì mỗi cung là một nửa đường tròn.
- Cung nằm bên trong gọi là cung bị chắn. Góc bẹt chắn nửa đường tròn.
Ví dụ:
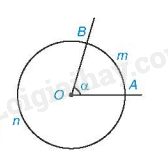
Trong hình trên, là cung nhỏ, ta có thể kí hiệu gọn là .
là cung lớn.
Ta nói góc AOB chắn cung AB hay cung AB bị chắn bởi góc AOB.
Cách xác định số đo một cung
Số đo của một cung được xác định như sau:
- Số đo của nửa đường tròn bằng .
- Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
- Số đo cung lớn bằng hiệu giữa và số đo của cung nhỏ có chung hai mút.
Ví dụ: Số đo của cung AB được kí hiệu là sđ.
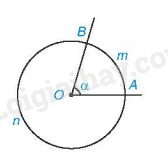
sđ; sđ.
Chú ý:
- Cung có số đo còn được gọi là cung . Cả đường tròn được coi là cung . Đôi khi ta cũng coi một điểm là cung .
- Hai cung trên một đường tròn gọi là bằng nhau nếu chúng có cùng số đo.
Xem thêm các chương trình khác:
- Soạn văn 9 Kết nối tri thức (hay nhất)
- Văn mẫu 9 - Kết nối tri thức
- Tóm tắt tác phẩm Ngữ văn 9 – Kết nối tri thức
- Tác giả tác phẩm Ngữ văn 9 - Kết nối tri thức
- Bố cục tác phẩm Ngữ văn 9 – Kết nối tri thức
- Nội dung chính tác phẩm Ngữ văn 9 – Kết nối tri thức
- Soạn văn 9 Kết nối tri thức (ngắn nhất)
- Bài tập Tiếng Anh 9 Global success theo Unit có đáp án
- Giải sgk Tiếng Anh 9 - Global success
- Trọn bộ Từ vựng Tiếng Anh 9 Global success đầy đủ nhất
- Trọn bộ Ngữ pháp Tiếng Anh 9 Global success đầy đủ nhất
- Giải sbt Tiếng Anh 9 – Global Success
- Giải sgk Khoa học tự nhiên 9 – Kết nối tri thức
- Lý thuyết Khoa học tự nhiên 9 – Kết nối tri thức
- Giải sbt Khoa học tự nhiên 9 – Kết nối tri thức
- Giải sgk Lịch sử 9 – Kết nối tri thức
- Giải sbt Lịch sử 9 – Kết nối tri thức
- Giải sgk Địa lí 9 – Kết nối tri thức
- Giải sbt Địa lí 9 – Kết nối tri thức
- Giải sgk Tin học 9 – Kết nối tri thức
- Giải sbt Tin học 9 – Kết nối tri thức
- Giải sgk Công nghệ 9 – Kết nối tri thức
- Giải sgk Giáo dục công dân 9 – Kết nối tri thức
- Giải sbt Giáo dục công dân 9 – Kết nối tri thức
- Giải sgk Hoạt động trải nghiệm 9 – Kết nối tri thức