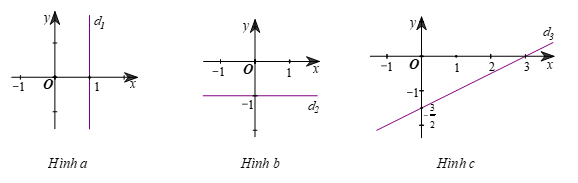Sách bài tập Toán 9 Bài 1 (Kết nối tri thức): Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn

Giải SBT Toán 9 Bài 1: Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn

Bài 1.1 trang 4 sách bài tập Toán 9 Tập 1: Giả sử (x;y) là nghiệm của phương trình bậc nhất hai ẩn 4x – 2y = 6.

a) Hoàn thành bảng sau đây:

Từ đó suy ra 5 nghiệm của phương trình đã cho.

b) Biểu diễn y theo x. Từ đó cho biết phương trình đã cho có bao nhiêu nghiệm?

Lời giải:

a) Ta viết phương trình về dạng $y=\frac{4x-6}{2}$ hay y = 2x – 3.

Khi đó ta có:

⦁ Với x = ­–2 thì y = 2 . (–2) – 3 = –7.

⦁ Với x = ­–2 thì y = 2 . (–1) – 3 = –5.

⦁ Với x = 0 thì y = 2 . 0 – 3 = –3.

⦁ Với x = ­1 thì y = 2 . 1 – 3 = –1.

⦁ Với x = ­2 thì y = 2 . 2 – 3 = 1.

Điền các giá trị x, y tương ứng vào bảng, ta được bảng giá trị thỏa mãn:

b) Như phần a) ta đã biểu diễn y = 2x – 3. Với mỗi giá trị x, ta luôn tìm được một giá trị y tương ứng.

Vậy phương trình đã cho có vô số nghiệm.

Bài 1.2 trang 4 sách bài tập Toán 9 Tập 1: Viết nghiệm và biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn sau:

a) 3x – 2y = 5;

b) 0x + 2y = 4;

c) 2x + 0y = –3.

Lời giải:

a) Phương trình đã cho có dạng $y=\frac{3x-5}{2}$ hay y = 1,5x – 2,5.

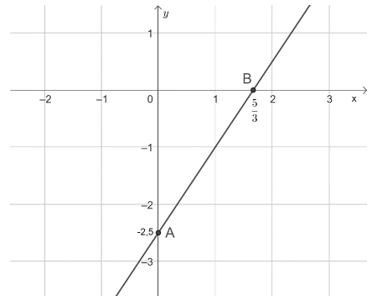
Nghiệm tổng quát của phương trình đã cho là (x; 1,5x – 2,5) với x ∈ ℝ. Mỗi nghiệm này là tọa độ một điểm thuộc đường thẳng d: 3x – 2y = 5.

Ta có hai điểm A(0; –2,5) và $B\left(\frac{5}{3};0\right)$ nằm trên đường thẳng d: 3x – 2y = 5 nên hình biểu diễn tất cả các nghiệm của phương trình đã cho là một đường thẳng đi qua 2 điểm A và B như hình dưới đây:

b) Phương trình đã cho có dạng 2y = 4 hay y = 2.

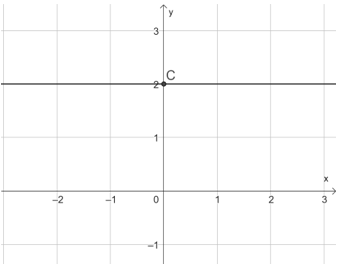
Nghiệm tổng quát của phương trình đã cho là (x; 2) với x ∈ ℝ. Mỗi nghiệm này là tọa độ một điểm thuộc đường thẳng d: 0x + 2y = 4. Đường thẳng này song song với trục hoành và cắt trục tung tại điểm C(0; 2).

Ta có hình biểu diễn tất cả các nghiệm của phương trình đã cho như hình dưới đây:

c) Phương trình đã cho có dạng 2x = –3 hay x = –1,5.

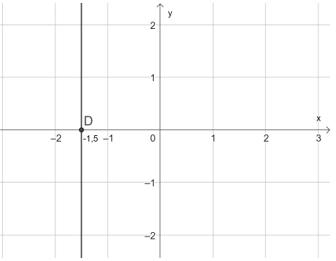
Nghiệm tổng quát của phương trình đã cho là (–1,5; y) với y ∈ ℝ. Mỗi nghiệm này là tọa độ một điểm thuộc đường thẳng d: 2x + 0y = –3. Đường thẳng này song song với trục tung và cắt trục hoành tại điểm D(–1,5; 0).

Ta có hình biểu diễn tất cả các nghiệm của phương trình đã cho như hình dưới đây:

Bài 1.3 trang 4 sách bài tập Toán 9 Tập 1: Cho phương trình bậc nhất hai ẩn mx + y = –2.

a) Xác định m để cặp số (1; –2) là một nghiệm của phương trình đã cho.

b) Viết công thức nghiệm tổng quát của phương trình với m tìm được ở câu a.

Lời giải:

a) Vì (1; –2) là một nghiệm của phương trình đã cho nên ta có:

m . 1 + (–2) = –2 hay m – 2 = –2, suy ra m = –2 + 2 = 0.

Vậy với m = 0 thì cặp số (1; –2) là một nghiệm của phương trình đã cho.

b) Với m = 0, ta được:

0 . x + y = –2 hay y = –2.

Vậy phương trình có nghiệm tổng quát là (x; ­–2) với x ∈ ℝ tùy ý.

Bài 1.4 trang 4 sách bài tập Toán 9 Tập 1: Bác Hương bán hàng tạp hoá và có (đủ nhiều) các tờ tiền lẻ loại 2 nghìn đồng và 5 nghìn đồng. Bác cần trả lại cho một người mua hàng 25 nghìn đồng.

a) Gọi x là số tờ tiền loại 2 nghìn đồng, y là số tờ tiền loại 5 nghìn đồng mà bác Hương cần trả lại cho khách (x, y ∈ ℕ). Hãy lập phương trình bậc nhất hai ẩn đối với x và y.

b) Hãy chỉ ra một nghiệm (x; y) với x, y ∈ ℕ của phương trình lập ở câu a để tìm một phương án trả lại tiền thừa cho khách giúp bác Hương.

Lời giải:

a) Theo đề bài, ta có phương trình bậc nhất hai ẩn đối với x và y biểu thị số tiền 25 nghìn đồng mà bác Hương trả lại cho người mua:

2x + 5y = 25

b) Phương trình trên còn được viết dưới dạng $y=\frac{25-2x}{5}$ hay y = 5 – 0,4x.

Xét các giá trị của x:

⦁ Với x = 1 thì y = 5 – 0,4 . 1 = 4,6 (loại).

⦁ Với x = 2 thì y = 5 – 0,4 . 2 = 4,2 (loại).

⦁ Với x = 3 thì y = 5 – 0,4 . 3 = 3,8 (loại).

⦁ Với x = 4 thì y = 5 – 0,4 . 4 = 3,4 (loại).

⦁ Với x = 5 thì y = 5 – 0,4 . 5 = 3 (chọn).

Vậy bác Hương có thể trả lại 25 nghìn đồng tiền thừa cho người mua bằng 5 tờ tiền 2 nghìn đồng và 3 tờ tiền 5 nghìn đồng.

Bài 1.5 trang 4 sách bài tập Toán 9 Tập 1: Một đội công nhân cần phải lắp đường ống dẫn nước trên một đoạn phố thẳng dài 65 m. Có hai loại ống dài 3 m và 5 m. Hãy chỉ ra ít nhất hai phương án lắp ống để không cần phải cưa ống ra (coi rằng các mối nối là không đáng kể).

Lời giải:

Gọi x là số ống loại 3 m và y là số ống loại 5 m cần dùng (x, y ∈ ℕ).

Theo đề bài, ta có phương trình bậc nhất hai ẩn x và y như sau: 3x + 5y = 65.

Phương trình trên còn có thể biểu diễn dưới dạng $y=\frac{65-3x}{5}$ hay y = 13 – 0,6x.

Ta lập được bảng giá trị như sau:

Vậy có thể dùng hai phương án để lắp ống cho đoạn phố: Phương án thứ nhất là dùng 5 ống loại 3 m và 10 ống loại 5 m; phương án thứ hai là dùng 10 ống loại 3 m và 7 ống loại 5 m.

Bài 1.6 trang 4 sách bài tập Toán 9 Tập 1: Cho các cặp số: (–2; 2), (1; 1), (4; 1), (8; –2) và hai phương trình:

x + 3y = 4; (1)

2x – 5y = –3. (2)

a) Những cặp số nào là nghiệm của phương trình (1)?

b) Cặp số nào là nghiệm của hệ gồm hai phương trình (1) và (2)?

c) Vẽ hai đường thẳng d: x + 3y = 4 và d': 2x – 5y = –3 trên cùng một mặt phẳng toạ độ để minh hoạ kết quả của câu b.

Lời giải:

a) Thay lần lượt các cặp số đã cho vào phương trình (1) ta được:

⦁ Với x = –2, y = 2: –2 + 3 . 2 = 4 nên (–2; 2) là nghiệm của phương trình (1).

⦁ Với x = 1, y = 1: 1 + 3 . 1 = 4 nên (1; 1) là nghiệm của phương trình (1).

⦁ Với x = 4, y = 2: 4 + 3 . 1 = 7 ≠ 4 nên (4; 1) không là nghiệm của phương trình (1).

⦁ Với x = 8, y = –2: 8 + 3 . (–2) = 2 ≠ 4 nên (8; –2) không là nghiệm của phương trình (1).

Vậy các cặp số (–2; 2), (1; 1) là nghiệm của phương trình (1).

b) Để cặp số là nghiệm của hệ gồm hai phương trình (1) và (2), cặp số cần thỏa mãn vừa là nghiệm của phương trình (1) vừa là nghiệm của phương trình (2).

Xét hai cặp số là nghiệm của phương trình (1):

⦁ Với x = –2, y = 2: 2. (–2) – 5 . 2 = –14 ≠ –3 nên (–2; 2) là không nghiệm của phương trình (2).

⦁ Với x = 1, y = 1: 2. 1 – 5 . 1 = –3 nên (1; 1) là nghiệm của phương trình (2).

Vậy cặp số (1; 1) là nghiệm của hệ phương trình gồm (1) và (2).

Bài 1.7 trang 4 sách bài tập Toán 9 Tập 1: Tìm a và b để hai phương trình ax – 2y = 1 và x + by = 3 nhận cặp số (1; –2) làm nghiệm chung.

Lời giải:

⦁ Thay cặp số (1; –2) vào phương trình ax – 2y = 1, ta được:

a . 1 – 2 . (–2) = 1 hay a – (–4) = 1, suy ra a = 1 + –4 = –3.

⦁ Thay cặp số (1; –2) vào phương trình x + by = 3, ta được:

1 + b. (–2) = 3 hay 1 – 2b = 3, suy ra $b=\frac{1-3}{2}=-1$.

Vậy với a = –3 và b = –1 thì hai phương trình ax – 2y = 1 và x + by = 3 nhận cặp số (1; –2) làm nghiệm chung.

Bài 1.8 trang 4 sách bài tập Toán 9 Tập 1: Bằng cách vẽ các đường thẳng thích hợp trên cùng một mặt phẳng toạ độ, hãy tìm nghiệm của mỗi hệ phương trình sau:

a) $\left\{\begin{array}{c}2x=-4\\ 3x-y=5\end{array}\right.$;

b) $\left\{\begin{array}{c}x-2y=4\\ 2y=-3\end{array}\right.$.

Lời giải:

a) Phương trình 2x = –4 còn có thể viết dưới dạng x = –2. Nghiệm tổng quát của phương trình này là (–2; y) với y ∈ ℝ. Mỗi nghiệm này là tọa độ một điểm thuộc đường thẳng d: 2x = –4. Đường thẳng này song song với trục tung và cắt trục hoành tại điểm A(–2; 0).

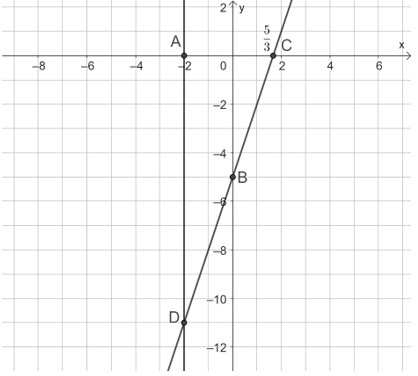
Phương trình 3x – y = 5 còn có thể viết dưới dạng y = 3x – 5. Nghiệm tổng quát của phương trình này là (x; 3x – 5) với x ∈ ℝ. Mỗi nghiệm này là tọa độ một điểm thuộc đường thẳng d: 3x – y = 5. Ta có hai điểm B(0; –5) và $C\left(\frac{5}{3};0\right)$ nằm trên đường thẳng d: 3x – y = 5.

Nghiệm của hệ phương trình là giao điểm của hai đường thẳng ở trên. Ta thấy trên hình vẽ đó là điểm D(–2; –11).

b) Phương trình 2y = –3 còn có thể viết dưới dạng y = –1,5.

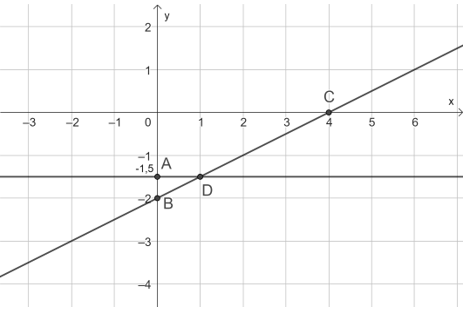
Nghiệm tổng quát của phương trình này là (x; –1,5) với x ∈ ℝ. Mỗi nghiệm này là tọa độ một điểm thuộc đường thẳng d: 2y = –3. Đường thẳng này song song với trục hoành và cắt trục tung tại điểm A(0; –1,5).

Phương trình x – 2y = 4 còn có thể viết dưới dạng x = 2y + 4.

Nghiệm tổng quát của phương trình này là (2y + 4; y) với y ∈ ℝ. Mỗi nghiệm này là tọa độ một điểm thuộc đường thẳng d: x – 2y = 4. Ta có hai điểm B(0; –2) và C(4; 0) nằm trên đường thẳng d: x – 2y = 4.

Nghiệm của hệ phương trình là giao điểm của hai đường thẳng ở trên. Ta thấy trên hình vẽ đó là điểm D(1; –1,5).

Lý thuyết Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn

1. Phương trình bậc nhất hai ẩn

Khái niệm phương trình bậc nhất hai ẩn: Phương trình bậc nhất hai ẩn x và y là hệ thức dạng ax + by = c (1), trong đó a, b và c là các số đã biết (a ≠ 0 hoặc b ≠ 0).

Khái niệm nghiệm của phương trình bậc nhất hai ẩn: Nếu tại x = x₀ và y = y₀ ta có ax₀ + by₀ = c là một khẳng định đúng thì cặp số (x₀; y₀) được gọi là một nghiệm của phương trình (1).

Chú ý: Một phương trình bậc nhất hai ẩn đều có vô số nghiệm.

Ví dụ 1. Các phương trình x = 1; 2y = –3; x – 2y = 3 là các phương trình bậc nhất hai ẩn x, y.

Phương trình 0x + 0y = 1 không là phương trình bậc nhất hai ẩn.

Ví dụ 2. Trong các cặp số sau, cặp số nào là nghiệm của phương trình x – 2y = 3?

a) (1; 2);

b) (–1; –2);

c) (3; 0).

Hướng dẫn giải

⦁ Thay x = 1 và y = 2, ta có: 1 – 2.2 = –3 ≠ 3.

Vậy (1; 2) không là nghiệm của phương trình đã cho.

⦁ Thay x = –1 và y = –2, ta có: –1 – 2.(–2) = 3.

Vậy (–1; –2) là một nghiệm của phương trình đã cho.

⦁ Thay x = 3 và y = 0, ta có: 3 – 2.0 = 3.

Vậy (3; 0) là một nghiệm của phương trình đã cho.

Nhận xét: Trong mặt phẳng tọa độ, tập hợp các điểm có tọa độ (x; y) thỏa mãn phương trình bậc nhất hai ẩn ax + by = c là một đường thẳng. Đường thẳng đó gọi là đường thẳng ax + by = c.

Ví dụ 3. Viết nghiệm và biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn sau:

a) x + 0y = 1.

b) 0x + y = –1.

c) x – 2y = 3.

Hướng dẫn giải:

a) Xét phương trình x + 0y = 1. (1)

Ta viết gọn (1) thành x = 1. Phương trình này có nghiệm là (1; y) với y ∈ ℝ tùy ý.

Mỗi nghiệm này là tọa độ của một điểm thuộc đường thẳng song song với trục tung và cắt trục hoành tại điểm (1; 0). Ta gọi đó là đường thẳng d₁: x = 1 (hình a).

b) Xét phương trình 0x + y = –1. (2)

Ta viết gọn (2) thành y = –1. Phương trình này có nghiệm là (x; –1) với x ∈ ℝ tùy ý.

Mỗi nghiệm này là tọa độ của một điểm thuộc đường thẳng song song với trục hoành và cắt trục tung tại điểm (0; –1). Ta gọi đó là đường thẳng d₂: y = –1 (hình b).

c) Xét phương trình x – 2y = 3. (3)

Ta viết (3) dưới dạng $y=\frac{1}{2}x-\frac{3}{2}.$ Mỗi cặp số $\left(x;\frac{1}{2}x-\frac{3}{2}\right)$ với x ∈ ℝ tùy ý, là một nghiệm của (3). Khi đó ta nói phương trình (3) có nghiệm tổng quát là $\left(x;\frac{1}{2}x-\frac{3}{2}\right)$ với x ∈ ℝ tùy ý.

Mỗi nghiệm này là tọa độ của một điểm thuộc đường thẳng $y=\frac{1}{2}x-\frac{3}{2}.$ Ta cũng gọi đường thẳng này là đường thẳng d₃: x – 2y = 3.

Để vẽ đường thẳng đó, ta chỉ cần xác định hai điểm tùy ý của nó, chẳng hạn $\left(0;-\frac{3}{2}\right)$ và (3; 0), rồi vẽ đường thẳng đi qua hai điểm đó (hình c).

2. Hệ hai phương trình bậc nhất hai ẩn

Khái niệm hệ hai phương trình bậc nhất hai ẩn: Một cặp gồm hai phương trình bậc nhất hai ẩn ax + by = c và a’x + b’y = c’ được gọi là một hệ hai phương trình bậc nhất hai ẩn. Ta thường viết hệ phương trình đó dưới dạng: $\left\{\begin{array}{l}ax+by=c\\ a^{\text{'}}x+b^{\text{'}}y=c^{\text{'}}.\end{array}\right.\left(*\right)$

Ví dụ 4. Trong các hệ phương trình sau, hệ nào không phải là hệ phương trình bậc nhất hai ẩn? Vì sao?

a) $\left\{\begin{array}{l}\sqrt{2}x+y=1\\ y=2.\end{array}\right.$

b) $\left\{\begin{array}{l}x+y=-1\\ 0x+0y=2.\end{array}\right.$

c)$\left\{\begin{array}{l}x-2y=3\\ -4x+5y=-6.\end{array}\right.$

Hướng dẫn giải

Hệ phương trình $\left\{\begin{array}{l}x+y=-1\\ 0x+0y=2\end{array}\right.$không phải là hệ phương trình bậc nhất hai ẩn vì phương trình thứ hai của hệ là 0x + 0y = 2 không phải là phương trình bậc nhất hai ẩn.

Khái niệm nghiệm của hệ hai phương trình bậc nhất hai ẩn: Mỗi cặp số (x₀; y₀) được gọi là một nghiệm của hệ (*) nếu nó đồng thời là nghiệm của cả hai phương trình của hệ (*).

Lưu ý: Mỗi nghiệm của hệ (*) chính là một nghiệm chung của hai phương trình của hệ (*).

Chú ý: Cặp số (x₀; y₀) là nghiệm của hệ phương trình (*) có nghĩa là điểm có tọa độ (x₀; y₀) vừa thuộc đường thẳng ax + by = c, vừa thuộc đường thẳng a’x + b’y = c’. Vậy điểm có tọa độ (x₀; y₀) là giao điểm của hai đường thẳng ax + by = c và a’x + b’y = c’.

Ví dụ 5. Cho hệ phương trình bậc nhất hai ẩn: $\left\{\begin{array}{l}x-y=20\\ 10x-7y=24.\end{array}\right.$

Trong các cặp số sau, cặp số nào là nghiệm của hệ phương trình đã cho?

a) (0; –20);

b) $\left(-\frac{116}{3};-\frac{176}{3}\right).$

Hướng dẫn giải

a) Ta thấy khi x = 0 và y = –20 thì:

0 – (–20) = 20 nên (0; –20) là nghiệm của phương trình thứ nhất;

10.0 – 7.(–20) = 140 ≠ 24 nên (0; –20) không là nghiệm của phương trình thứ hai.

Do đó cặp số (0; –20) không là nghiệm chung của hai phương trình trong hệ.

Vậy cặp số (0; –20) không là nghiệm của hệ phương trình đã cho.

b) Ta thấy khi $x=-\frac{116}{3}$ và $y=-\frac{176}{3}$ thì:

$-\frac{116}{3}–\left(–\frac{176}{3}\right)=20$ nên $\left(-\frac{116}{3};-\frac{176}{3}\right)$ là nghiệm của phương trình thứ nhất;

$10\cdot \left(-\frac{116}{3}\right)–7\cdot \left(–\frac{176}{3}\right)=24$ nên $\left(-\frac{116}{3};-\frac{176}{3}\right)$ là nghiệm của phương trình thứ hai.

Suy ra cặp số $\left(-\frac{116}{3};-\frac{176}{3}\right)$ là nghiệm chung của hai phương trình trong hệ.

Vậy cặp số $\left(-\frac{116}{3};-\frac{176}{3}\right)$ là nghiệm của hệ phương trình đã cho.