Sách bài tập Toán 9 Bài 6 (Kết nối tri thức): Bất phương trình bậc nhất một ẩn

Giải SBT Toán 9 Bài 6: Bất phương trình bậc nhất một ẩn

Bài 2.14 trang 28 sách bài tập Toán 9 Tập 1: Giải các bất phương trình:

a) –7x + 3 > 0;

b) 6x + 5 > 0;

c) $-\frac{1}{2}x+7<0$;

d) $\frac{2}{5}x+3\le 0$.

Lời giải:

a) –7x + 3 > 0

–7x > –3

$x<\frac{-3}{-7}$

$x<\frac{3}{7}$

Vậy $x<\frac{3}{7}$.

b) 6x + 5 > 0

6x > –5

$x>-\frac{5}{6}$

Vậy $x>-\frac{5}{6}$.

c) $-\frac{1}{2}x+7<0$

$-\frac{1}{2}x<-7$

$x>\left(-7\right):\left(-\frac{1}{2}\right)$

X > 14

Vậy x > 14.

d) $\frac{2}{5}x+3\le 0$

$\frac{2}{5}x\le -3$

$x\le \left(-3\right):\frac{2}{5}$

$x\le -\frac{15}{2}$

Vậy $x\le -\frac{15}{2}$.

Bài 2.15 trang 28 sách bài tập Toán 9 Tập 1: Giải các bất phương trình:

a) –5x + 3 > 2x + 5;

b) 6x² – 5x + 1 ≤ 6x² + 4x + 3

Lời giải:

a) –5x + 3 > 2x + 5;

–5x – 2x > 5 – 3

–7x > 2

$x<\frac{2}{-7}$

$x<-\frac{2}{7}$

Vậy $x<-\frac{2}{7}$.

b) 6x² – 5x + 1 ≤ 6x² + 4x + 3

–5x + 1 ≤ 4x + 3

–5x – 4x ≤ 3 – 1

–9x ≤ 2

$x\ge \frac{2}{-9}$

$x\ge -\frac{2}{9}$

Vậy $x\ge -\frac{2}{9}$.

Bài 2.16 trang 28 sách bài tập Toán 9 Tập 1: Giải các bất phương trình:

a) 3(2x – 3)(2x + 3) > 12x² + 2x;

b) (2x + 1)(5x – 3) > 10x² + 2x + 1.

Lời giải:

a) 3(2x – 3)(2x + 3) > 12x² + 2x

3(4x² – 9) > 12x² + 2x

12x² – 27 > 12x² + 2x

–27 > 2x

2x < –27

$x<-\frac{27}{2}$.

Vậy $x<-\frac{27}{2}$.

b) (2x + 1)(5x – 3) > 10x² + 2x + 1.

10x² – x – 3 > 10x² + 2x + 1.

–x – 3 > 2x + 1

–x – 2x > 1 + 3

–3x > 4

$x<\frac{4}{-3}$

$x<-\frac{4}{3}$.

Vậy $x<-\frac{4}{3}$.

Bài 2.17 trang 28 sách bài tập Toán 9 Tập 1: Một công ty chuyền nhà cần di chuyển một cây đàn piano nặng 260 kg bằng thang máy. Thang máy có thể chở được tối đa là 710 kg.

a) Viết và giải bất phương trình để xác định khối lượng thang máy có thể chở thêm được.

b) Ngoài chiếc đàn piano, thang máy có thề chở thêm được bao nhiêu người biết mỗi người nặng khoảng 60 kg.

Lời giải:

a) Gọi x (kg) là khối lượng thang máy có thể chở thêm được.

Khối lượng thang máy chở được là x + 260.

Vì thang máy chở được tối đa 710 kg nên:

x + 260 ≤ 710

x ≤ 710 – 260

x ≤ 450.

Vậy thang máy có thể chở thêm được tối đa 450 kg.

b) Gọi y là số người thang máy có thể chở thêm được ($y\in \mathbb{N}*$).

Khối lượng người thang máy chở là 60y (kg).

Thang máy có thể chở thêm tối đa 450 kg nên ta có:

60y ≤ 450

$y\le \frac{450}{60}$

$y\le \frac{15}{2}=7,5$

Suy ra y = 7.

Vậy thang máy có thể chở thêm tối đa 7 người nữa.

Bài 2.18 trang 28 sách bài tập Toán 9 Tập 1: David có thể kiếm được 8 USD cho mỗi giờ làm việc tại công ty chuyên chăm sóc cây cảnh và anh ấy muốn kiếm được ít nhất 1 200 USD trong mùa hè này.

a) Hãy viết một bất phương trình mô tả tình huống này.

b) Hỏi anh ấy cần làm việc ít nhất bao nhiêu giờ để kiếm được số tiền trên?

Lời giải:

a) Gọi số giờ làm việc của David là x (giờ).

Số tiền David kiếm được là 8x (USD).

David muốn kiếm ít nhất 1 200 đô nên ta có:

8x ≥ 1 200

b) Giải bất phương trình trên ta được:

8x ≥ 1 200

$x\ge \frac{1200}{8}$

x ≥ 150

Vậy David cần làm việc ít nhất 150 giờ để kiếm được ít nhất 1 200 USD trong mùa hè này.

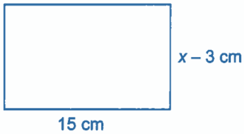
Bài 2.19 trang 28 sách bài tập Toán 9 Tập 1: Chiều dài của một hình chữ nhật thì luôn lớn hơn hoặc bằng chiều rộng. Hãy viết và giải bất phương trình để tìm giá trị có thể của x (cm) trong hình vẽ dưới đây:

Lời giải:

Vì chiều dài hình chữ nhật luôn lớn hơn hoặc bằng chiều rộng nên ta có:

x – 3 ≤ 15

x ≤ 15 + 3

x ≤ 18 (1)

Chiều rộng hình chữ nhật phải là một số dương nên ta có:

x – 3 > 0

x > 3 (2)

Từ (1) và (2) ta được: 3 < x ≤ 18.

Vậy các giá trị có thể có của x là 3 < x ≤ 18.

Lý thuyết Bất phương trình bậc nhất một ẩn

1. Khái niệm bất phương trình bậc nhất một ẩn

1.1. Khái niệm bất phương trình bậc nhất một ẩn

Bất phương trình dạng ax + b < 0 (hoặc ax + b > 0, ax + b ≤ 0, ax + b ≥ 0), trong đó a, b là hai số đã cho, a ≠ 0 được gọi là bất phương trình bậc nhất một ẩn (ẩn x).

Ví dụ 1. Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn x?

a) –2x+4 ≤ 0;

b) $3-\frac{3}{2}x<0;$

c) x³ + 1 ≥ 0.

Lời giải:

Bất phương trình ở câu a), b) là bất phương trình bậc nhất một ẩn x.

Bất phương trình ở câu c) không là bất phương trình bậc nhất một ẩn x vì x³ là đa thức bậc ba.

1.2. Nghiệm của bất phương trình bậc nhất một ẩn

• Số x₀ là một nghiệm của bất phương trình A(x) > B(x) nếu A(x₀) > B(x₀) là khẳng định đúng.

• Giải một bất phương trình là tìm tất cả các nghiệm của bất phương trình đó.

Ví dụ 2. Trong các số $\frac{1}{2};–2;4$, giá trị nào là nghiệm của bất phương trình 2x – 3 ≥ 0.

Hướng dẫn giải

• Thay $x=\frac{1}{2}$ vào bất phương trình 2x – 3 ≥ 0, ta được $2\cdot \frac{1}{2}–3\ge 0$ là khẳng định sai.

Do đó, $x=\frac{1}{2}$ không là nghiệm của bất phương trình đã cho.

• Thay x = –2 vào bất phương trình 2x – 3 ≥ 0, ta được 2 . (–2) – 3 ≥ 0 là khẳng định sai.

Do đó, x = –2 không là nghiệm của bất phương trình đã cho.

• Thay x = 4 vào bất phương trình 2x – 3 ≥ 0, ta được 2 . 4 – 3 ≥ 0 là khẳng định đúng.

Do đó, x = 4 là nghiệm của bất phương trình đã cho.

Vậy trong các số đã cho thì x = 4 là nghiệm của bất phương trình 2x – 3 ≥ 0.

2. Cách giải bất phương trình bậc nhất một ẩn

Bất phương trình bậc nhất một ẩn ax + b > 0 (a ≠ 0) được giải như sau:

ax + b < 0

ax < −b.

• Nếu a > 0 thì $x<-\frac{b}{a}.$

• Nếu a < 0 thì $x>-\frac{b}{a}.$

Chú ý: Các bất phương trình ax + b > 0, ax + b ≤ 0, ax + b ≥ 0 được giải tương tự.

Ví dụ 3. Giải bất phương trình: 11x – 5 < 0.

Hướng dẫn giải

Ta có:11x – 5 < 0

11x < 5

$x<\frac{5}{11}$.

Vậy nghiệm của bất phương trình là $x<\frac{5}{11}$.

Chú ý: Ta cũng có thể giải được cácbất phương trình một ẩn đưa được về dạng ax + b < 0,ax + b > 0, ax + b ≤ 0, ax + b ≥ 0.

Ví dụ 4. Giải bất phương trình: 2x – 5 < 2 – 3x.

Hướng dẫn giải

Ta có: 2x – 5 < 2 – 3x

2x + 3x < 5 + 2

5x < 7

$x<\frac{7}{5}$.

Vậy nghiệm của bất phương trình là $x<\frac{7}{5}$.