Sách bài tập Toán 9 Bài 11 (Kết nối tri thức): Tỉ số lượng giác của góc nhọn
Với giải sách bài tập Toán 9 Bài 11: Tỉ số lượng giác của góc nhọn sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 9 Bài 11.
Giải SBT Toán 9 Bài 11: Tỉ số lượng giác của góc nhọn
Bài 4.1 trang 45 sách bài tập Toán 9 Tập 1:
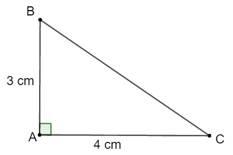
a) Vẽ tam giác ABC vuông tại A, AB = 3 cm, AC = 4 cm. Tính BC, sin B, cos B.
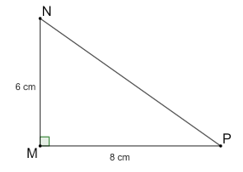
b) Vẽ tam giác MNP vuông tại M, MN = 6 cm, MP = 8 cm. Hỏi hai tam giác ABC, MNP có đồng dạng không? Tính sin N, cos N.
Lời giải:
a)
Theo định lý Pythagore, ta có: BC2 = AB2 + AC2 = 32 + 42 = 25.
Suy ra BC=√25=5(cm).
Từ đó ta có: sinB=ACBC=45, cosB=ABBC=35
Vậy BC = 5 cm, sinB=45, cosB=35.
b)
Ta thấy: MNMP=68=34=ABAC
Suy ra hai tam giác vuông MNP và ABC đồng dạng vì có hai cặp cạnh góc vuông tương ứng tỷ lệ.
Từ đó suy ra sinN=sinB=ACBC=45, cosP=cosB=ABBC=35
Vậy hai tam giác MNP và ABC đồng dạng, sinN=45, cosP=35
Bài 4.2 trang 45 sách bài tập Toán 9 Tập 1:
a) Chứng minh rằng với mọi góc nhọn α < 45°, ta có
sin (45°– α) = cos (45° + α), cos (45° – α) = sin (45° + α).
b) Không dùng MTCT, tính
sin 25° + sin 35° + sin 45° – cos 45° – cos 55° – cos 65°.
Lời giải:
a) Ta thấy (45° – α) + (45° + α) = 90°, suy ra đây là hai góc phụ nhau.
Do đó sin (45° – α) = cos (45° + α), cos (45°– α) = sin (45° + α).
b) sin 25° + sin 35° + sin 45° – cos 45° – cos 55° – cos 65°.
= (sin 25°– cos 65°) + (sin 35° – cos 55°) + (sin 45° – cos 45°) = 0.
Bài 4.3 trang 45 sách bài tập Toán 9 Tập 1: Khi góc α lần lượt bằng 10°, 20°, 30°, 40°, hãy dùng MTCT tính sin α trong mỗi trường hợp (làm tròn đến chữ số thập phân thứ ba).
Lời giải:
+ Để tính sin 10°, ta sử dụng MTCT bấm liên tiếp các phím:
Ta được sin 10° ≈ 0,174.
+ Để tính sin 20°, ta sử dụng MTCT bấm liên tiếp các phím:
Ta được sin 20° ≈ 0,342.
+ Để tính sin 30°, ta sử dụng MTCT bấm liên tiếp các phím:
Ta được sin 30° ≈ 0,500.
+ Để tính sin 40°, ta sử dụng MTCT bấm liên tiếp các phím:
Ta được sin 40° ≈ 0,643.
Bài 4.4 trang 45 sách bài tập Toán 9 Tập 1: Hãy dùng MTCT, tìm số đo của góc nhọn α (làm tròn đến độ) trong mỗi trường hợp
a) Khi sin α lần lượt bằng 14,
b) Khi cos α lần lượt bằng
Lời giải:
a) Sử dụng MTCT bấm liên tiếp các phím:
Ta được thì α ≈ 14°.
Tương tự, ta tính được:
thì α ≈ 19°.
thì α =30°.
thì α ≈ 42°.
b) Sử dụng MTCT bấm liên tiếp các phím:
Ta được thì α ≈ 76°.
Tương tự, ta tính được:
thì α ≈ 71°.
thì α ≈ 60°.
thì α ≈ 48°.
Bài 4.5 trang 45 sách bài tập Toán 9 Tập 1: Biết rằng với mỗi góc nhọn α, ta có sin2 α + cos2 α = 1, không dùng MTCT, hãy tính sin2 25° + sin2 35° + sin2 45° + sin2 55° + sin2 65°.
Lời giải:
Do các góc phụ nhau có sin α = cos (90°– α) nên ta có:
sin 65° = cos 25°, sin 55° = cos 35°
Ta có:
sin2 25° + sin2 35° + sin2 45° + sin2 55° + sin2 65°.
= sin2 25° + sin2 35° + sin2 45° + cos2 35° + cos2 25°
= (sin2 25° + cos2 25°) + (sin2 35° + cos2 35°) + sin2 45°
= 1 + 1 + 0,5
= 2,5.
Vậy sin2 25° + sin2 35° + sin2 45° + sin2 55° + sin2 65° = 2,5.
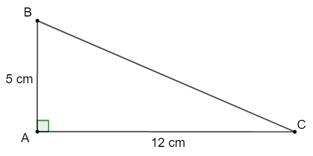
Bài 4.6 trang 45 sách bài tập Toán 9 Tập 1: Một tam giác vuông có hai cạnh góc vuông đo được 5 cm, 12 cm. Hỏi sin của góc nhọn nhỏ nhất của tam giác đó bằng bao nhiêu?
Lời giải:
Xét tam giác vuông ABC có AB = 5 cm, AC = 12 cm. Góc nhọn cần tính là góc C.
Áp dụng định lý Pythagore, ta có:
(cm)
Do đó
Vậy sin của góc nhọn nhỏ nhất trong tam giác đó bằng
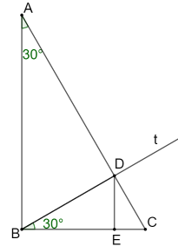
Bài 4.7 trang 45 sách bài tập Toán 9 Tập 1: Xét tam giác ABC vuông tại B, có = 30°. Tia Bt sao cho = 30° cắt tia AC ở D, D nằm giữa A và C. Chứng minh rằng khoảng cách từ D đến đường thẳng BC bằng
Lời giải:
Do đó tam giác BDC và tam giác ABD vuông tại D.
+ Xét tam giác vuông ABD, ta có:
Gọi E là chân đường vuông góc kẻ từ D tới BC.
Khi đó ta có DE là khoảng cách từ D đến đường thẳng BC.
+ Xét tam giác vuông BDE, ta có:
Ta có: , suy ra (đpcm).
Bài 4.8 trang 45 sách bài tập Toán 9 Tập 1: Vẽ góc α trong mỗi trường hợp:
a) cos α = 0,4;
b) tan α = ;
c) .
Lời giải:
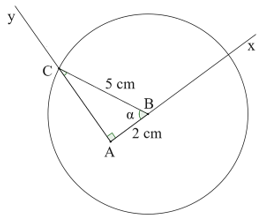
a) Ta thấy:
Suy ra góc α tương ứng với góc B của tam giác ABC vuông tại A với độ dài AB = 2 cm, BC = 5 cm.
Vẽ góc vuông Axy, lấy B trên tia Ax sao cho AB = 3 cm.
Vẽ đường tròn tâm B bán kính 5 cm. Lấy C là giao điểm của đường tròn này với tia Ay.
Góc B của tam giác ABC chính là góc α.
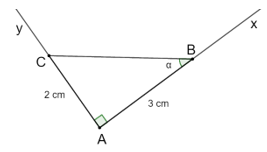
b) Ta có:
Góc α tương ứng với góc B của tam giác ABC vuông tại A với độ dài AC = 2 cm, AB = 3 cm.
Vẽ góc vuông Axy, lấy B trên tia Ax sao cho AB = 3 cm. Lấy C trên tia Ay sao cho AC = 2 cm.
Góc B của tam giác ABC chính là góc α.
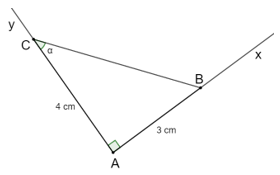
c) Góc α tương ứng với góc C của tam giác ABC vuông tại A với độ dài AB = 3 cm, AC = 4 cm.
Vẽ góc vuông Axy, lấy B trên tia Ax sao cho AB = 3 cm.
Lấy C trên tia Ay sao cho AC = 4 cm.
Góc C của tam giác ABC chính là góc α.
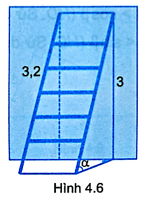
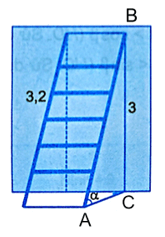
Bài 4.9 trang 45 sách bài tập Toán 9 Tập 1: Một cái thang dài 3,2 m đặt tựa bức tường, đầu thang đạt đến độ cao 3 m thì thang tạo với mặt đất góc α xấp xỉ bằng bao nhiêu độ (H.4.6)?
Lời giải:
Gọi vị trí chân thang là điểm A, đầu thang là điểm B và hình chiếu vuông góc của đầu thang với mặt đất là điểm C.
Ta thấy AB = 3,2 m, BC = 3 m và tam giác ACB vuông tại C.
Ta có
Dùng MTCT tính được α ≈ 70°.
Vậy thang tạo với mặt đất góc α xấp xỉ bằng 70°.
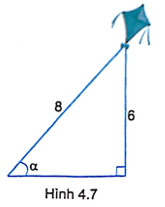
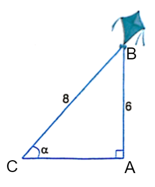
Bài 4.10 trang 46 sách bài tập Toán 9 Tập 1: Một cái diều có dây diều dài 8 m, khi dây diều căng thì diều bay ở độ cao 6 m. Hỏi khi đó dây diều tạo với phương ngang của mặt đất góc nhọn α xấp xỉ bằng bao nhiêu độ (H.4.7)?
Lời giải:
Gọi vị trí của điều là B, đầu dây diều là C, hình chiếu vuông góc của diều tới phương ngang của đầu dây điều là A.
Ta thấy BC = 8 m, AB = 6 m và tam giác BAC vuông tại A.
Ta có:
Dùng MTCT tính được α ≈ 49°.
Vậy khi đó dây diều tạo với phương ngang của mặt đất góc nhọn α xấp xỉ bằng 49°.
Bài 4.11 trang 46 sách bài tập Toán 9 Tập 1: Chứng minh tam giác vuông có một góc nhọn có tang bằng 1 là tam giác vuông cân.
Lời giải:
Xét tam giác ABC vuông tại A có tan B = 1.
Khi đó ta có: hay AB = AC.
Suy ra tam giác ABC vuông cân tại A.
Vậy tam giác vuông có một góc nhọn có tang bằng 1 là tam giác vuông cân.
Bài 4.12 trang 46 sách bài tập Toán 9 Tập 1:
a) Tính các góc của tam giác vuông có một góc nhọn có tang bằng
b) Một hình chữ nhật có kích thước 3 và . Tính các góc tạo bởi đường chéo và cạnh của hình chữ nhật đó.
Lời giải:
a) Gọi . Suy ra α = 30°.
Góc nhọn còn lại là 90° – 30° = 60°.
Vậy hai góc nhọn của tam giác vuông đó có độ lớn là 30° và 60°.
b) Đường chéo hình chữ nhật chia hình chữ nhật thành 2 hình tam giác với độ dài 2 cạnh là 3 và
Gọi hai góc tạo bởi đường chéo hình chữ nhật và hai cạnh hình chữ nhật là α và 90° – α.
Đặt
Theo câu a, ta có α = 30° và 90° – α = 60°.
Vậy hai góc tạo bởi đường chéo hình chữ nhật với cạnh của hình chữ nhật đó có độ lớn là 30° và 60°.
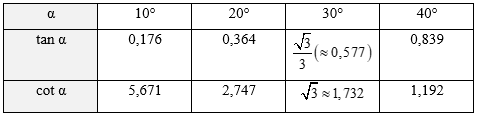
Bài 4.13 trang 46 sách bài tập Toán 9 Tập 1: Dùng MTCT, hãy tìm tang và côtang của góc nhọn α khi α lần lượt bằng 10°, 20°, 30°, 40° (làm tròn đến chữ số thập phân thứ ba)
Lời giải:
Sử dụng MTCT, ta tìm được tang và côtang của góc nhọn α, sau đó làm tròn đến chữ số thập phân thứ ba.
Ta có bảng giá trị như sau:
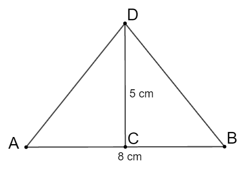
Bài 4.14 trang 46 sách bài tập Toán 9 Tập 1: Tính tang, côtang của góc kề đáy của tam giác cân biết cạnh đáy dài 8 cm, đường cao ứng với đáy dài 5 cm.
Lời giải:
Xét tam giác ADB cân tại D có AB = 8 cm, C là trung điểm AB.
Suy ra DC vuông góc với AB hay tam giác ACD vuông tại C và DC = 5 cm.
(cm).
Xét tam giác vuông ACD, ta có: ,
Vậy tan và cotan của góc kề đáy của tam giác đó có giá trị lần lượt là và
Bài 4.15 trang 46 sách bài tập Toán 9 Tập 1: Dùng định nghĩa tỉ số lượng giác sin α, cos α, tan α, cot α hãy chứng minh rằng:
a) ,
b)
Lời giải:
a) Xét tam giác ABC vuông tại A với góc B là góc α, ta có:
Khi đó:
Vậy (đpcm).
b) (định vì AB2 + AC2 = BC2).
Suy ra sin2 α + cos2 α = 1.
Do đó (dpcm).
Bài 4.16 trang 46 sách bài tập Toán 9 Tập 1: Cho góc α có tan α = . Tính sin α, cos α.
Lời giải:
Ta có
Suy ra hay
Vì suy ra
Vậy
Bài 4.17 trang 46 sách bài tập Toán 9 Tập 1: Với α < β < 90°, chứng minh rằng:
a) cos α > cos β (HD. Sử dụng Ví dụ 5 và bài 4.15);
b) sin α < sin β (HD. Sử dụng công thức sin2 α + cos2 α = 1).
Lời giải:
Theo Ví dụ 5, khi số đo góc nhọn α tăng lên thì tan α tăng nên, suy ra với α < β < 90° thì tan α > tan β.
a) Ta có:
cos α > cos β (đpcm).
b) Theo câu a ta có: cos α > cos β
sin α < sin β (đpcm).
Lý thuyết Tỉ số lượng giác của góc nhọn
1. Khái niệm tỉ số lượng giác của một góc nhọn
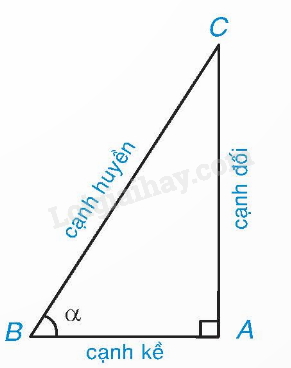
|
. gọi là các tỉ số lượng giác của góc nhọn . |
Tip học thuộc nhanh:
|
Sin đi học Cos không hư Tan đoàn kết Cotan kết đoàn |
Chú ý: Nếu là một góc nhọn thì ; ; ;
Ví dụ:
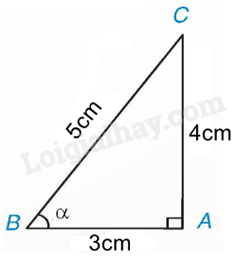
Theo định nghĩa của tỉ số lượng giác, ta có:
, , ,
Giá trị lượng giác của các góc
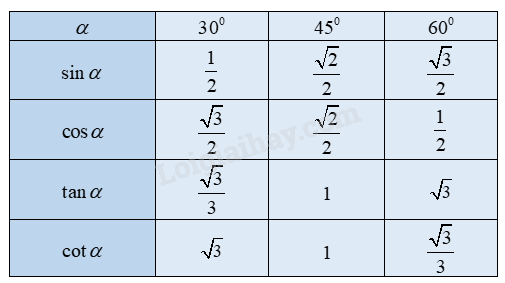
2. Tỉ số lượng giác của hai góc phụ nhau
Định lí về tỉ số lượng giác của hai góc phụ nhau
|
Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tan góc này bằng côtang góc kia. |
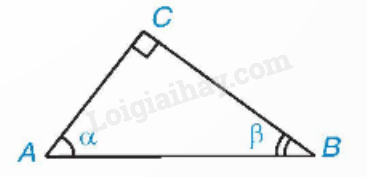
Cho và là hai góc phụ nhau, ta có:
, , , .
Ví dụ:
3. Sử dụng máy tính cầm tay tính tỉ số lượng giác của một góc nhọn
Sử dụng máy tính cầm tay để tính các tỉ số lượng giác

Sử dụng máy tính cầm tay để tìm được góc khi biết một trong các tỉ số lượng giác của góc đó
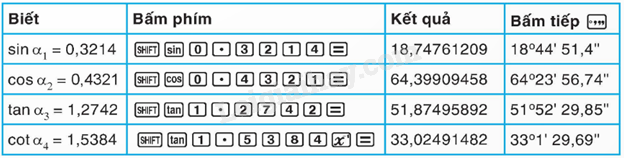
Một số công thức mở rộng:
+)
+)
+)
+)
+)
+)
Xem thêm các chương trình khác:
- Soạn văn 9 Kết nối tri thức (hay nhất)
- Văn mẫu 9 - Kết nối tri thức
- Tóm tắt tác phẩm Ngữ văn 9 – Kết nối tri thức
- Tác giả tác phẩm Ngữ văn 9 - Kết nối tri thức
- Bố cục tác phẩm Ngữ văn 9 – Kết nối tri thức
- Nội dung chính tác phẩm Ngữ văn 9 – Kết nối tri thức
- Soạn văn 9 Kết nối tri thức (ngắn nhất)
- Bài tập Tiếng Anh 9 Global success theo Unit có đáp án
- Giải sgk Tiếng Anh 9 - Global success
- Trọn bộ Từ vựng Tiếng Anh 9 Global success đầy đủ nhất
- Trọn bộ Ngữ pháp Tiếng Anh 9 Global success đầy đủ nhất
- Giải sbt Tiếng Anh 9 – Global Success
- Giải sgk Khoa học tự nhiên 9 – Kết nối tri thức
- Lý thuyết Khoa học tự nhiên 9 – Kết nối tri thức
- Giải sbt Khoa học tự nhiên 9 – Kết nối tri thức
- Giải sgk Lịch sử 9 – Kết nối tri thức
- Giải sbt Lịch sử 9 – Kết nối tri thức
- Giải sgk Địa lí 9 – Kết nối tri thức
- Giải sbt Địa lí 9 – Kết nối tri thức
- Giải sgk Tin học 9 – Kết nối tri thức
- Giải sbt Tin học 9 – Kết nối tri thức
- Giải sgk Công nghệ 9 – Kết nối tri thức
- Giải sgk Giáo dục công dân 9 – Kết nối tri thức
- Giải sbt Giáo dục công dân 9 – Kết nối tri thức
- Giải sgk Hoạt động trải nghiệm 9 – Kết nối tri thức