Sách bài tập Toán 9 Bài 2 (Kết nối tri thức): Giải hệ hai phương trình bậc nhất hai ẩn

Giải SBT Toán 9 Bài 2: Giải hệ hai phương trình bậc nhất hai ẩn

Bài 1.9 trang 12 sách bài tập Toán 9 Tập 1: Giải các hệ phương trình sau bằng phương pháp thế::

a) $\left\{\begin{array}{c}x+2y=8\\ \frac{1}{2}x-y=18\end{array}\right.$;

b) $\left\{\begin{array}{c}0,2x+0,5y=0,7\\ 4x+10y=9\end{array}\right.$;

c) $\left\{\begin{array}{c}-2x+3y=1\\ \frac{1}{3}x-\frac{1}{2}y=-\frac{1}{6}\end{array}\right.$.

Lời giải:

a) Từ phương trình x + 2y = 8, ta có x = 8 – 2y.

Thế vào phương trình $\frac{1}{2}x-y=18$ ta được:

$\frac{1}{2}\left(8-2y\right)-y=18$

4 – y – y = 18

4 – 2y = 18

2y = –14

y = 7

Từ đó ta được x = 8 – 2 . (–7) = 22.

Vậy nghiệm của hệ phương trình là (22; –7).

b) Từ phương trình 0,2x + 0,5y = 0,7, ta có $x=\frac{0,7-0,5y}{0,2}=3,5-2,5y$.

Thế vào phương trình 4x + 10y = 9 ta được:

4x + 10y = 9

4 . (3,5 – 2,5y) + 10y = 9

14 + 0.y = 9 (vô nghiệm)

Vậy hệ phương trình đã cho vô nghiệm.

c) Từ phương trình –2x + 3y = 1, ta có $x=\frac{3y-1}{2}=\frac{3}{2}y-\frac{1}{2}$.

Thế vào phương trình $\frac{1}{3}x-\frac{1}{2}y=-\frac{1}{6}$ ta được:

$\frac{1}{3}x-\frac{1}{2}y=-\frac{1}{6}$

$\frac{1}{3}\left(\frac{3}{2}y-\frac{1}{2}\right)-\frac{1}{2}y=-\frac{1}{6}$

$0y-\frac{1}{6}=\frac{-1}{6}$ (vô số nghiệm)

Xét phương trình –2x + 3y = 1, ta được $y=\frac{1+2x}{3}=\frac{1}{3}+\frac{2}{3}x$.

Vậy hệ phương trình đã cho có nghiệm $\left(x;\frac{1}{3}+\frac{2}{3}x\right)$ với $x\in ℝ$ tùy ý.

Bài 1.10 trang 12 sách bài tập Toán 9 Tập 1: Giải các hệ phương trình sau bằng phương pháp cộng đại số:

a) $\left\{\begin{array}{c}3x-7y=-14\\ 5x+2y=45\end{array}\right.$;

b) $\left\{\begin{array}{c}x-0,5y=-3\\ 2x-y=6\end{array}\right.$;

c) $\left\{\begin{array}{c}2x+3y=3\\ \frac{2}{3}x+y=1\end{array}\right.$.

Lời giải:

a) Nhân hai vế của phương trình thứ nhất với 2 và phương trình thứ hai với 7, ta được:

$\left\{\begin{array}{c}6x-14y=-28\\ 35x+14y=315\end{array}\right.$

Cộng từng vế của hai phương trình trên, ta được:

41x = 287 hay $x=\frac{287}{41}=7$.

Thay vào phương trình thứ nhất, ta được:

6 . 7 – 14y = –28 hay 42 – 14y = –28, suy ra $y=\frac{42-\left(-28\right)}{14}=5$.

Vậy nghiệm của hệ phương trình là (7; 5).

b) Nhân hai vế của phương trình thứ nhất với –2, ta được:

$\left\{\begin{array}{c}-2x+y=6\\ 2x-y=6\end{array}\right.$

Cộng từng vế của hai phương trình trên, ta được:

0x + 0y = –12 (vô nghiệm)

Vậy hệ phương trình đã cho vô nghiệm.

c) Nhân hai vế của phương trình thứ hai với –3, ta được:

$\left\{\begin{array}{c}2x+3y=3\\ -2x-3y=-3\end{array}\right.$

Cộng từng vế của hai phương trình trên, ta được:

0x + 0y = 0 (vô số nghiệm)

Xét phương trình 2x + 3y = 3, ta có $y=\frac{3-2x}{3}=1-\frac{2}{3}x$

Vậy hệ phương trình đã cho có nghiệm $\left(x;1-\frac{2}{3}x\right)$ với $x\in ℝ$ tùy ý.

Bài 1.11 trang 12 sách bài tập Toán 9 Tập 1: Sử dụng MTCT, tìm nghiệm của các hệ phương trình sau:

a) $\left\{\begin{array}{c}\sqrt{3}x+3y=1\\ 2x-\sqrt{3}y=\sqrt{3}\end{array}\right.$;

b) $\left\{\begin{array}{c}2,5x-3,5y=0,5\\ -0,5x+0,7y=1\end{array}\right.$;

c) $\left\{\begin{array}{c}\frac{x}{5}+\frac{y}{2}=5\\ 0,4x+y=1\end{array}\right.$.

Lời giải:

a) Hệ phương trình đã cho có nghiệm là $\left(\frac{4\sqrt{3}}{9};-\frac{1}{9}\right)$.

b) Hệ phương trình đã cho vô nghiệm.

c) Hệ phương trình đã cho vô nghiệm.

Bài 1.12 trang 13 sách bài tập Toán 9 Tập 1: Tìm a và b để đường thẳng y = ax + b đi qua hai điểm (4; 1) và (–4; –3).

Lời giải:

Vì đường thẳng y = ax + b đi qua hai điểm (4; 1) và (–4; –3) nên ta lập được hệ phương trình bậc nhất hai ẩn như sau:

$\left\{\begin{array}{c}4a+b=1\\ -4a+b=-3\end{array}\right.$

Cộng từng vế của hai phương trình trên, ta được:

2b = –2 hay $b=\frac{-2}{2}=-1$.

Thay b = –1 vào phương trình thứ nhất, ta được:

4a – 1 = 1 hay $a=\frac{1+1}{4}=\frac{1}{2}$.

Vậy với $a=\frac{1}{2}$ và b = –1 thì đường thẳng y = ax + b đi qua hai điểm (4; 1) và (–4; –3).

Bài 1.13 trang 13 sách bài tập Toán 9 Tập 1: Cho hệ phương trình $\left\{\begin{array}{c}x+3y=1\\ 2x+my=5\end{array}\right.$

a) Giải hệ với m = 1.

b) Chứng tỏ rằng hệ đã cho vô nghiệm khi m = 6.

Lời giải:

a) Với m = 1, ta có: $\left\{\begin{array}{c}x+3y=1\\ 2x+y=5\end{array}\right.$.

Nhân hai vế của phương trình thứ nhất với –2, ta được:

$\left\{\begin{array}{c}-2x-6y=-2\\ 2x+y=5\end{array}\right.$.

Cộng từng vế của hai phương trình trên, ta được:

–5y = 3 hay y = $\frac{3}{-5}=-\frac{3}{5}$.

Thay vào phương trình thứ nhất, ta được:

$x+3.\left(-\frac{3}{5}\right)=1$ hay $x-\frac{9}{5}=1$, suy ra $x=1+\frac{9}{5}=\frac{14}{5}$.

Vậy hệ phương trình đã cho có nghiệm là $\left(\frac{14}{5};-\frac{3}{5}\right)$ với m = 1.

b) Với m = 6, ta có: $\left\{\begin{array}{c}x+3y=1\\ 2x+6y=5\end{array}\right.$.

Nhân hai vế của phương trình thứ nhất với –2, ta được: $\left\{\begin{array}{c}-2x-6y=-2\\ 2x+6y=5\end{array}\right.$

Cộng từng vế của hai phương trình trên, ta được:

0x+0y = 3 (vô nghiệm).

Vậy hệ phương trình đã cho vô nghiệm khi m = 6.

Bài 1.14 trang 13 sách bài tập Toán 9 Tập 1: Trong kinh tế học, đường IS là một phương trình bậc nhất biểu diễn tất cả các kết hợp thu nhập Y và lãi suất r để duy trì trạng thái cân bằng của thị trường hàng hoá trong nền kinh tế. Đường LM là một phương trình bậc nhất biểu diễn tất cả các kết hợp giữa thu nhập Y và lãi suất r duy trì trạng thái cân bằng của thị trường tiền tệ trong nền kinh tế. Trong một nền kinh tế, giả sử mức thu nhập cân bằng Y (tính bằng triệu đô la) và lãi suất cân bằng r thoả mãn hệ phương trình

$\left\{\begin{array}{c}0,06Y-5000r=240\\ 0,06Y+6000r=900\end{array}\right.$

Tìm mức thu nhập và lãi suất cân bằng.

Lời giải:

Ta có hệ phương trình $\left\{\begin{array}{c}0,06Y-5 000r=240\\ 0,06Y+6 000r=900\end{array}\right.$.

Trừ từng vế của phương trình thứ hai cho phương trình thứ nhất của hệ, ta được:

11 000r = 660 hay $r=\frac{660}{11 000}=0,06$.

Thay vào phương trình thứ nhất, ta được:

0,06Y – 5 000 . 0,06 = 240 hay 0,06Y – 300 = 240.

Suy ra $Y=\frac{240+300}{0,06}=9 000$.

Vậy mức thu nhập cân bằng là 9 000 tiệu đô la và lãi suất cân bằng là 0,06.

Bài 1.15 trang 13 sách bài tập Toán 9 Tập 1: Phương trình cung và phương trình cầu của một loại thiết bị kĩ thuật số cá nhân mới là:

Phương trình cầu: p = 150 – 0,00001x;

Phương trình cung: p = 60 + 0,00002x;

trong đó p là giá mỗi đơn vị sản phẩm (tính bằng đô la) và x là số lượng đơn vị sản phẩm. Tìm điểm cân bằng của thị trường này, tức là điểm (p; x) thoả mãn cả hai phương trình cung và cầu.

Lời giải:

Ta có hệ phương trình $\left\{\begin{array}{c}p=150-0,00001x\\ p=60+0,00002x\end{array}\right.$

Trừ từng vế của phương trình thứ nhất cho phương trình thứ hai, ta được:

0 = 90 – 0,00003x hay $x=\frac{90}{0,00003}=3 000 000$.

Thay vào phương trình thứ nhất, ta được:

p = 150 – 0,00001 . 3 000 000 = 120.

Vậy điểm cân bằng của thị trường này là (120; 3 000 000).

Bài 1.16 trang 13 sách bài tập Toán 9 Tập 1: Thầy Nam dạy Toán đang thiết kế một bài kiểm tra trắc nghiệm gồm hai loại câu hỏi, câu hỏi đúng/sai và câu hỏi nhiều lựa chọn. Bài kiểm tra sẽ được tính trên thang điểm 100, trong đó mỗi câu hỏi đúng/sai có giá trị 2 điểm và mỗi câu hỏi nhiều lựa chọn có giá trị 4 điểm. Thầy Nam muốn số câu hỏi nhiều lựa chọn gấp đôi số câu hỏi đúng/sai.

a) Gọi số câu hỏi đúng/sai là x, số câu hỏi nhiều lựa chọn là y (x, y ∈ ℕ*). Viết hệ hai phương trình biểu thị số lượng của từng loại câu hỏi.

b) Giải hệ phương trình trong câu a để biết số lượng câu hỏi mỗi loại trong bài kiểm tra là bao nhiêu.

Lời giải:

a) Số câu hỏi nhiều lựa chọn gấp đôi số câu hỏi đúng/sai nên y = 2x hay 2x – y = 0.

Tổng điểm bài kiểm tra là 2x + 4y = 100.

Từ đó ta lập được hệ phương trình: $\left\{\begin{array}{c}2x-y=0\\ 2x+4y=100\end{array}\right.$.

b) Trừ từng vế phương trình thứ nhất cho phương trình thứ hai, ta được:

–5y = – 100 hay $y=\frac{-100}{-5}=20$.

Thay vào phương trình thứ nhất, ta được:

2x – 20 = 0 hay x = $\frac{0+20}{2}=10$.

Vây bài kiểm tra có 10 câu hỏi đúng/sai và 20 câu hỏi nhiều lựa chọn.

Lý thuyết Giải hệ hai phương trình bậc nhất hai ẩn

1. Phương pháp thế

Cách giải hệ phương trình bằng phương pháp thế:

Bước 1. Từ một phương trình của hệ, biểu diễn một ẩn theo ẩn kia rồi thế vào phương trình còn lại của hệ để được phương trình chỉ còn chứa một ẩn.

Bước 2. Giải phương trình một ẩn vừa nhận được, từ đó suy ra nghiệm của hệ phương trình đã cho.

Ví dụ 1. Giải hệ phương trình $\left\{\begin{array}{l}2x+3y=7\\ x-10y=-8\end{array}\right.$bằng phương pháp thế.

Hướng dẫn giải

Giải hệ phương trình $\left\{\begin{array}{l}2x+3y=7\left(1\right)\\ x-10y=-8\left(2\right)\end{array}\right.$

Từ phương trình (2), ta có: x = 10y – 8. (3)

Thế vào phương trình (1) ta được: 2.(10y – 8) + 3y = 7. (4)

Giải phương trình (4):

2.(10y – 8) + 3y = 7

20y – 16 + 3y = 7

23y = 23

y = 1.

Thay y = 1 vào phương trình (3), ta có:

x = 10.1 – 8 = 2.

Vậy hệ phương trình đã cho có nghiệm duy nhất (2; 1).

2. Phương pháp cộng đại số

Cách giải hệ phương trình bằng phương pháp cộng đại số:

Để giải một hệ hai phương trình bậc nhất hai ẩn có hệ số của cùng một ẩn nào đó trong hai phương trình bằng nhau hoặc đối nhau, ta có thể làm như sau:

Bước 1. Cộng hay trừ từng vế của hai phương trình trong hệ để được phương trình chỉ còn chứa một ẩn.

Bước 2. Giải phương trình một ẩn vừa nhận được, từ đó suy ra nghiệm của hệ phương trình đã cho.

Chú ý: Trường hợp trong hệ phương trình đã cho không có hai hệ số của cùng một ẩn bằng nhau hay đối nhau, ta có thể đưa về trường hợp đã xét bằng cách nhân hai về của mỗi phương trình với một số thích hợp (khác 0).

Ví dụ 2. Giải hệ phương trình $\left\{\begin{array}{l}2x+3y=7\\ x-10y=-8\end{array}\right.$bằng phương pháp cộng đại số.

Hướng dẫn giải

Xét hệ phương trình $\left\{\begin{array}{l}2x+3y=7\left(1\right)\\ x-10y=-8\left(2\right)\end{array}\right.$

Nhân hai vế của phương trình (2) với 2, ta được hệ phương trình sau: $\left\{\begin{array}{l}2x+3y=7\left(3\right)\\ 2x-20y=-16\left(4\right)\end{array}\right.$

Trừ từng vế hai phương trình (3) và (4), ta nhận được phương trình:

23y = 23, tức là y = 1.

Thay y = 1 vào phương trình (2), ta có: x – 10.1 = –8. (5)

Giải phương trình (5):

x – 10.1 = –8

x – 10 = –8

x = 2.

Vậy hệ phương trình đã cho có nghiệm duy nhất (2; 1).

3. Sử dụng máy tính cầm tay để tìm nghiệm của hệ hai phương trình bậc nhất hai ẩn

Cách tìm nghiệm của hệ hai phương trình bậc nhất hai ẩn bằng máy tính cầm tay

Muốn tìm nghiệm của hệ hai phương trình bậc nhất hai ẩn bằng máy tính cầm tay (MTCT), chúng ta cần sử dụng loại máy có chức năng này (thường có phím MODE). Trước hết ta phải viết hệ phương trình cần tìm nghiệm dưới dạng: $\left\{\begin{array}{l}{a}_{1}x+b_{1}y=c_1\\ a_{2}x+b_{2}y=c_2.\end{array}\right.$

Chẳng hạn, để tìm nghiệm của hệ $\left\{\begin{array}{l}2x-3y-4=0\\ 5x-6y-7=0\end{array}\right.,$ ta viết nó dưới dạng $\left\{\begin{array}{l}2x-3y=4\\ 5x-6y=7\end{array}\right..$

Khi đó, ta có a₁ = 2, b₁ = 3, c₁ = 4; a₂ = 5, b₂ = 6 và c₂ = 7. Lần lượt thực hiện các bước sau (với máy tính thích hợp):

Bước 1. Vào chức năng giải hệ hai phương trình bậc nhất hai ẩn bằng cách bấm các phím (xem màn hình sau bước 1, con trỏ ở vị trí a₁).

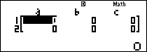
Bước 2. Nhập các số a₁ = 2, b₁ = 3, c₁ = 4; a₂ = 5, b₂ = 6 và c₂ = 7 bằng cách bấm: (xem màn hình sau bước 2).

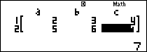
Bước 3. Đọc kết quả: Sau khi kết thúc bước 2, bấm , màn hình cho x = –1; bấm tiếp phím , màn hình cho y = 2 (xem màn hình sau bước 3). Ta hiểu nghiệm của hệ phương trình là (–1; 2).

Chú ý:

– Muốn xóa số vừa nhập thì bấm phím muốn thay đổi số đã nhập ở một vị trí nào đó thì di chuyển con trỏ đến vị trí đó rồi nhập số mới.

– Bấm phím hay để chuyển đổi hiển thị các giá trị của x và y trong kết quả.

– Nếu máy báo “Infinite Sol” thì hệ phương trình đã cho có vô số nghiệm. Nếu máy báo “No-Solution” thì hệ phương trình đã cho vô nghiệm.