Nội dung bài viết

    Xem thêm

    Lý thuyết Thứ tự trong tập hợp số nguyên – Toán lớp 6 Chân trời sáng tạo

    Với lý thuyết Toán lớp 6 Bài 2: Thứ tự trong tập hợp số nguyên chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sách Chân trời sáng tạo sẽ giúp học sinh nắm vững kiến thức trọng tâm để học tốt môn Toán 6.

    1 637 24/04/2023
    Trang trước
    Chia sẻ
    Trang sau  

    A. Lý thuyết Toán 6 Bài 2: Thứ tự trong tập hợp số nguyên - Chân trời sáng tạo

    1. So sánh hai số nguyên

    Khi biểu diễn hai số nguyên a, b trên trục số nằm ngang, nếu điểm a nằm bên trái điểm b thì ta nói a nhỏ hơn b hoặc b lớn hơn a và ghi là: a < b hoặc b > a.

    Ví dụ:

    Thứ tự trong tập hợp số nguyên | Lý thuyết Toán lớp 6 Chân trời sáng tạo (ảnh 1)

    Số −4 nằm bên trái số −2 nên ta nói −4 nhỏ hơn −2 và ghi là −4 < −2, hoặc ta nói −4 lớn hơn −2 và ghi −4 > −2.

    Nhận xét:

    − Mọi số nguyên dương đều lớn hơn 0.

    − Mọi số nguyên âm đều nhỏ hơn 0.

    − Mọi số nguyên âm đều nhỏ hơn bất kì số nguyên dương nào.

    − Với hai số nguyên âm, số nào có số đối lớn hơn thì số đó nhỏ hơn.

    Ví dụ: So sánh các cặp số sau:

    a) 5 và −20;

    b) −16 và −4.

    Hướng dẫn giải

    a) 5 là số nguyên dương và −20 là số nguyên âm nên 5 > −20.

    Vậy 5 > −20.

    b) Số đối của số −16 và −4 lần lượt là 16 và 4.

    Vì 16 > 4 nên −16 < −4.

    Vậy −16 < −4.

    2. Thứ tự trong tập hợp số nguyên

    Ví dụ: Sắp xếp các số − 5; 4; −2; 0; 2 theo thứ tự tăng dần.

    Hướng dẫn giải

    Ta xếp các số thành các nhóm rồi so sánh:

    Nhóm 1: Các số nguyên âm: – 5 và – 2.

    Số đối của – 5 và – 2 lần lượt là 5 và 2.

    Vì 5 > 2 nên – 5 < – 2.

    Do đó – 5 < – 2 < 0.

    Nhóm 2: Các số nguyên dương: 4 và 2.

    Ta có 2 < 4. Khi đó 0 < 2 < 4.

    Do đó: – 5 < – 2 < 0 < 2 < 4.

    Vậy các số đã cho được sắp xếp theo thứ tự tăng dần là: –5; –2; 0; 2; 4.

    Bài tập tự luyện

    Bài 1: So sánh các cặp số sau:

    a) – 15 và 0;

    b) 7 và −8;

    b) −21 và −6.

    Hướng dẫn giải

    a) – 15 < 0 (số nguyên âm luôn nhỏ hơn 0);

    b) 7 > −8 (số nguyên dương lớn hơn số nguyên âm);

    b) Số đối của số −21 và −6 lần lượt là 21 và 6.

    Vì 21 > 6 nên −21 < −6.

    Vậy −21 < −6.

    Bài 2. Sắp xếp các số nguyên sau theo thứ tự tăng dần.

    3; − 4; 5; 4; 12; 0; − 1; − 10; − 8.

    Hướng dẫn giải

    * Ta chia các số đã cho thành các nhóm rồi so sánh:

    Nhóm 1: Nhóm các số nguyên dương: 3; 5; 4; 12.

    Ta có 3 < 4 < 5 < 12.

    Khi đó 0 < 3 < 4 < 5 < 12. 

    Nhóm 2: Các số nguyên âm: – 4; – 1; – 10; – 8.

    Số đối của các số – 4; – 1; – 10; – 8 lần lượt là 4; 1; 10; 8.

    Vì 10 > 8 > 4 > 1 nên – 10 < – 8 < – 4 < – 1 < 0.

    Khi đó – 10 < – 8 < – 4 < – 1 < 0.

    Do đó ta có: – 10 < – 8 < – 4 < – 1 < 0 < 3 < 4 < 5 < 12.

    Vậy các số đã cho được sắp xếp theo thứ tự tăng dần là:

    – 10; – 8; – 4; – 1; 0; 3; 4; 5; 12.

    B. Trắc nghiệm Thứ tự trong tập hợp số nguyên (Chân trời sáng tạo 2023) có đáp án

    Câu 1. Số liền sau của số −5 là số

    A. 4                         

    B. −6                            

    C. −4                          

    D. −5

    Đáp án: C

    Giải thích:

    Ta thấy: −5 < −4 và không có số nguyên nào nằm giữa      −5 và −4
    Nên số liền sau của số −5  là số −4.

    Câu 2. Chọn câu đúng.

    A. 2 > 3  

    B. 3 < −2

    C. 0 < −3

    D. −4 < −3

    Đáp án: D

    Giải thích:

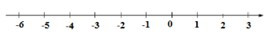
    TOP 40 câu Trắc nghiệm Thứ tự trong tập hợp số nguyên có đáp án - Toán lớp 6 Chân trời sáng tạo (ảnh 1)

    Điểm 2 nằm bên trái điểm 3 nên 2 < 3. Do đó A sai.   

    Điểm 3 nằm bên phải điểm −2 nên 3 > −2. Do đó B sai.

    Điểm 0 nằm bên trái điểm −3 nên 0> − 3. Do đó C sai.

    Điểm −4 nằm bên trái điểm −3 nên−4 < −3. Do đó D đúng.

    Câu 3. Số nguyên âm lớn nhất có 6 chữ số là

    A. −1000000    

    B. −10000  

    C. −100000 

    D. 100000

    Đáp án: C

    Giải thích:

    Số nguyên dương nhỏ nhất có 6 chữ số là: 100000.
    Nên số nguyên âm lớn nhất có 6 chữ số là: −100000.

    Câu 4. Khẳng định nào dưới đây đúng?

    A. Số nguyên a lớn hơn −4. Số aa chắc chắn là số dương

    B. Số nguyên a nhỏ hơn 3. Số aa chắc chắn là số âm

    C. Số nguyên a lớn hơn 1. Số aa chắc chắn là số dương

    D. Số nguyên a nhỏ hơn 0. Số aa có thể là số dương, có thể là số âm

    Đáp án: C

    Giải thích:

    Phương án A sai. Ví dụ −2 > −4 nhưng −2 là số nguyên âm.

    Phương án B sai. Ví dụ 1 < 3 nhưng 1 là số dương.

    Phương án D sai vì các số nguyên nhỏ hơn 0 là các số nguyên âm.

    Phương án C đúng.

    Câu 5. Trong các khẳng định sau, khẳng định nào đúng?

    A. −46718 < −46812

    B. −67523 < −66712

    C. −12 > 7

    D. −123 < −126

    Đáp án: B

    Giải thích:

    Do 67523 > 66712 nên −67523 < −66712.

    Khẳng định đúng là: B.

    Câu 6. Cho số nguyên aa lớn hơn −2 thì  số nguyên aa là

    A. Số nguyên dương

    B. Số tự nhiên

    C. Số nguyên âm

    D. Số −1 và số tự nhiên

    Đáp án: D

    Giải thích:

    TOP 40 câu Trắc nghiệm Thứ tự trong tập hợp số nguyên có đáp án - Toán lớp 6 Chân trời sáng tạo (ảnh 1)

    Các số lớn hơn −2 là các số −1;0;1;2;3;4;... nghĩa là gồm số −1 và các số tự nhiên.

    Câu 7. Viết tập hợp M = {x∈Z|−5 < x ≤ 3} dưới dạng liệt kê ta được

    A. M ={−5;−4;−3;−2;−1;0;1;3}                   

    B. M ={−4;−3;−2;−1;1;2;3}

    C. M ={−4;−3;−2;−1;0;1;2;3}          

    D. M ={−4;−3;−2;−1;0;1;2}

    Đáp án: C

    Giải thích:

    Các số nguyên lớn hơn −5  và nhỏ hơn hoặc bằng 3 là −4; −3; −2; −1; 0; 1; 2; 3.

    Nên M ={−4; −3; −2; −1; 0; 1; 2; 3}.

    Câu 8. Nếu a < b và b < c thì:

    A. a > c

    B. a < c

    C. a = c

    D. a ≥ c

    Đáp án: B

    Giải thích:

    Nếu a < b và b < c thì a < c.

    Câu 9. Khẳng định nào sau đây đúng?

    A. Nếu x < 3 thì x < 1

    B. Nếu x > 3 thì x > 5

    C. Nếu x > 2 thì x > −1

    D. Nếu x < 8 thì x < 5

    Đáp án: C

    Giải thích:

    Do x > 2 và 2 > −1 nên x > −1.

    Câu 10. Nếu a là số nguyên dương thì:

    A. a ≥ 0

    B. a > 0

    C. a < 0

    D. a ≤ 0

    Đáp án: B

    Giải thích:

    Nếu a là số nguyên dương thì: a > 0.

    Xem thêm tóm tắt lý thuyết Toán lớp 6 sách Chân trời sáng tạo hay, chi tiết khác:

    Tham khảo các loạt bài Toán 6 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 637 24/04/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: