Lý thuyết Dấu hiệu chia hết cho 3, cho 9 – Toán lớp 6 Chân trời sáng tạo
Với lý thuyết Toán lớp 6 Bài 8: Dấu hiệu chia hết cho 3, cho 9 chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sách Chân trời sáng tạo sẽ giúp học sinh nắm vững kiến thức trọng tâm để học tốt môn Toán 6.
A. Lý thuyết Toán 6 Bài 8: Dấu hiệu chia hết cho 3, cho 9 - Chân trời sáng tạo
1. Dấu hiệu chia hết cho 9
Các số có tổng các chữ số chia hết cho 9 thì số đó chia hết cho 9 và chỉ những số đó chia hết cho 9.
Ví dụ:
a) Số 1 944 chia hết cho 9 vì có tổng các chữ số là 1 + 9 + 4 + 4 = 18 chia hết cho 9.
b) Số 7 325 không chia hết cho 9 vì có tổng các chữ số là 7 + 3 + 2 + 5 = 17 không chia hết cho 9.
2. Dấu hiệu chia hết cho 3
Các số có tổng các chữ số chia hết cho 3 thì số đó chia hết cho 3 và chỉ những số đó chia hết cho 3.
Ví dụ:
a) Số 90 156 chia hết cho 3 vì có tổng các chữ số là 9 + 0 + 1 + 5 + 6 = 21 chia hết cho 3.
b) Số 6 116 không chia hết cho 3 vì có tổng các chữ số là 6 + 1 + 1 + 6 = 14 không chia hết cho 3.
Bài tập tự luyện
Bài 1. Cho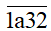 
chia hết cho 9. Tìm số thay thế cho a.
Hướng dẫn giải
Tổng các chữ số của 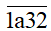là 1 + a + 3 + 2 = a + 6 = a + 6.
Nên để 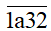chia hết cho 9 thì a + 6 phải chia hết cho 9.
Do a là các số tự nhiên từ 0 đến 9 nên:
0 + 6 ≤ a + 6 ≤ 9 + 6.
Hay 6 ≤ a + 6 ≤ 15.
Số chia hết cho 9 từ 6 đến 15 chỉ có đúng một số là 9 nên a + 6 = 9
Do đó a = 3.
Vậy số thay thế cho a chỉ có thể là 3.
Bài 2: Cho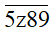 
chia hết cho 3 và chia hết cho 9. Hãy tìm chữ số z.
Hướng dẫn giải
Vì một số bất kỳ nếu chia hết cho 9 thì cũng chia hết cho 3 nên ta chỉ xét 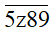chia hết cho 9.
Để 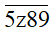⋮ 9 thì (5 + z + 8 + 9) ⋮ 9
Hay (22 + z) ⋮ 9 nên z = 5.
Vậy với z = 5 thì 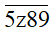chia hết cho 3 và chia hết cho 9.
Bài 3. Tổng (hiệu) sau chia hết cho 3 hay 9?
a) 1251 + 5316;
b) 5436 – 1324;
c) 1 . 2 . 3 . 4 . 5 . 6 + 27.
Hướng dẫn giải
a) Tổng các chữ số của 1251 là 1 + 2 + 5 + 1 = 9 chia hết cho 3 và 9.
Tổng các chữ số của 5 316 là 5 + 3 + 1 + 6 = 15 chia hết cho 3 nhưng không chia hết cho 9.
Vậy 1251 + 5316 chia hết cho 3 nhưng không chia hết cho 9.
b) Tổng các chữ số của 5436 có 5 + 4 + 3 + 6 = 18 chia hết cho 3 và 9.
Tổng các chữ số của 1324 có 1 + 3 + 2 + 4 = 10 không chia hết cho 3 và 9.
Vậy 5436 – 1324 không chia hết cho 3 và 9.
c) Tích 1 . 2 . 3 . 4 . 5 . 6 chia hết cho 3 (vì tích này có thừa số là 3).
Ta có: 1 . 2 . 3 . 4 . 5 . 6
= 1 . 2 . 3 . 4 . 5 . (3 . 2)
= 1 . 2 . 4 . 5 . (3 . 3) . 2
= 1 . 2 . 4 . 5 . 9 . 2 chia hết cho 9 (vì nó có thừa số là 9).
Do đó 1 . 2 . 3 . 4 . 5 . 6 chia hết cho 3 và 9.
Tổng các chữ số của 27 là 2 + 7 = 9 chia hết cho 3 và 9.
Vậy 1 . 2 . 3 . 4 . 5 . 6 + 27 chia hết cho 3 và 9.
B. Trắc nghiệm Dấu hiệu chia hết cho 3, cho 9 (Chân trời sáng tạo 2023) có đáp án
Câu 1. Hãy chọn câu sai:
A. Một số chia hết cho 9 thì số đó chia hết cho 3
B. Một số chia hết cho 3 thì số đó chia hết cho 9
C. Một số chia hết cho 10 thì số đó chia hết cho 5
D. Một số chia hết cho 45 thì số đó chia hết cho 9
Đáp án: B
Giải thích:
Câu sai là B: Số chia hết cho 3 thì chia hết cho 9. Chẳng hạn số 3 chia hết cho 3 nhưng số 3 không chia hết cho 9.
+ Mọi số chia hết cho 9 đều hia hết cho 3 nên A đúng.
+ Một số chia hết cho 10 thì số đó chia hết cho 5 vì các số chia hết cho 10 luôn có chữ số tận cùng là chữ số 0. Nên C đúng.
+ Một số chia hết cho 45 thì số đó chia hết cho 9 và chia hết cho 5 nên D đúng.
Câu 2. Cho chia hết cho 9. Số thay thế cho a có thể là
A. 1
B. 2
C. 3
D. 5
Đáp án: A
Giải thích:
Tổng các chữ số của là 1 + a +5 + 2 = a + 8 để số chia hết cho 9 thì a + 8 phải chia hết cho 9.
Do a là các số tự nhiên từ 0 đến 9 nên
0 + 8 ≤ a + 8 ≤ 9 + 8 ⇒ 8 ≤ a + 8 ≤ 17
Số chia hết cho 9 từ 8 đến 17 chỉ có đúng một số 9, do đó a + 8 = 9 ⇒ a = 1
Vậy số thay thế cho a chỉ có thể là 1.
Câu 3. Số vừa chia hết cho 2 vừa chia hết cho 9 là:
A. 10008
B. 152
C. 153
D. 2156
Đáp án: A
Giải thích:
Số chia hết cho 2 là: 10008, 152 và 2156
10008 có tổng các chữ số bằng 9 nên 10008 chia hết cho 9.
Câu 4. Trong những số sau, có bao nhiêu số chia hết cho 3?
555464, 15645, 5464, 561565, 641550
A. 1
B. 2
C. 4
D. 5
Đáp án: B
Giải thích:
555464 có tổng các chữ số là: 5+5+5+4+6+4 = 29 không chia hết cho 3 nên 555464 không chia hết cho 3.
15645 có tổng các chữ số là: 1+5+6+4+5 = 21 chia hết cho 3 nên 15645 chia hết cho 3
5464 có tổng các chữ số là: 5+4+6+4 = 19 không chia hết cho 3 nên 5464 không chia hết cho 3.
561565 có tổng các chữ số là: 5+6+1+5+6+5 = 28 không chia hết cho 3 nên 561565 không chia hết cho 3.
641550 có tổng các chữ số là: 6+4+1+5+5+0 = 21 chia hết cho 3 nên 641550 chia hết cho 3.
Vậy có tất cả 2 số chia hết cho 3 là: 15645 và 641550
Câu 5. Cho chia hết cho 3. Số thay thế cho a có thể là
A. 1
B. 2
C. 3
D. 5
Đáp án: C
Giải thích:
Tổng các chữ số của là 5 + 5 + a + 6 + 2 = a + 18
để số chia hết cho 3 thì a + 18 phải chia hết cho 3.
Do a là các số tự nhiên từ 0 đến 9 nên
0 + 18 ≤ a + 18 ≤ 9 + 18 ⇒ 18 ≤ a + 18 ≤ 27
Số chia hết cho 3 từ 18 đến 27 có thể là các số: 18, 21, 24, 27
Tức là a + 18 có thể nhận các giá trị: 18, 21, 24, 27
Với a + 18 bằng 18 thì a = 18 – 18 = 0
Với a + 18 bằng 21 thì a = 21 – 18 = 3
Với a + 18 bằng 24 thì a = 24 – 18 = 6
Với a + 18 bằng 27 thì a = 27 – 18 = 9
Vậy số có thể thay thế cho a là một trong các số 0; 3; 6; 9.
Vậy số thay thế cho a trong đề bài chỉ có thể là 3.
Câu 6. Các số có … chia hết cho 9 thì chia hết cho 9 và chỉ những số đó mới chia hết cho 9.
A. các chữ số
B. tổng các chữ số
C. tổng
D. chữ số tận cùng
Đáp án: B
Giải thích:
Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và chỉ những số đó mới chia hết cho 9.
Câu 7. Các số có tổng … chia hết cho 3 thì chia hết cho 3 và chỉ những số đó mới chia hết cho 3.
A. các chữ số
B. tổng các chữ số
C. các số
D. chữ số tận cùng
Đáp án: A
Giải thích:
Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3 và chỉ những số đó mới chia hết cho 3.
Câu 8. Khối lớp 6 của một trường có 255 học sinh đi dã ngoại. Cô phụ trách muốn chia đều các học sinh của khối 6 thành 9 nhóm. Hỏi cô chia như vậy đúng hay sai?
Đúng
Sai
Đáp án:
Giải thích:
Ta có 255 có tổng các chữ số bằng 2 + 5 + 5 = 12 không chia hết cho 9 nên cô phụ trách không thể chia đều số học sinh thành 9 nhóm được.
Câu 9. Trong các số 333; 354; 360; 2457; 1617; 152, các số chia hết cho 9 là
A. 333
B. 360
C. 2457
D. Cả A, B, C đều đúng
Đáp án: D
Giải thích:
Các số 333; 2457; 360 là các số chia hết cho 9 vì tổng các chữ số của nó chia hết cho 9.
+) Số 333 có tổng các chữ số là 3 + 3 + 3 = 9⁝9 nên 333⁝9.
+) Số 2457 có tổng các chữ số là 2 + 4 + 5 + 7 = 18⁝9 nên 2457⁝9.
+) Số 360 có tổng các chữ số là 3 + 6 + 0 = 9⁝9 nên 360⁝9.
Các số còn lại 354; 1617; 152 đều có tổng các chữ số không chia hết cho 9 nên chúng không chia hết cho 9.
Câu 10. Cho số . Tìm tổng các chữ số a và b sao cho A chia 9 dư 2.
A. (a + b) ϵ {9; 18}
B. (a + b) ϵ {0; 9; 18}
C. (a + b) ϵ {1; 2; 3}
D. (a + b) ϵ {4; 5; 6}
Đáp án: A
Giải thích:
Ta có: a; b ϵ {0; 1; 2; 3; 4; 5; 6; 7; 8; 9} và a ≠ 0.
A chia 9 dư 2 ⇒ a + 7 + 8 + 5 + b = a + b + 20 chia 9 dư 2 hay (a + b + 18)⁝9.
Mà 18⁝9 ⇒ (a + b)⁝9 ⇒ (a + b) ϵ {9; 18}.
Xem thêm tóm tắt lý thuyết Toán lớp 6 sách Chân trời sáng tạo hay, chi tiết khác:
Lý thuyết Bài 10: Số nguyên tố, Hợp số, Phân tích một số ra thừa số nguyên tố
Lý thuyết Bài 11: Ước chung, Ước chung lớn nhất
Xem thêm các chương trình khác:
- Soạn văn lớp 6 (hay nhất) - Chân trời sáng tạo
- Soạn văn lớp 6 (ngắn nhất) - Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn 6 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 6 – Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn lớp 6 - Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn 6 - Chân trời sáng tạo
- Văn mẫu lớp 6 – Chân trời sáng tạo
- Giải sgk Địa Lí 6 – Chân trời sáng tạo
- Giải sbt Địa Lí 6 – Chân trời sáng tạo
- Lý thuyết Địa Lí 6 – Chân trời sáng tạo
- Giải sgk Lịch sử 6 – Chân trời sáng tạo
- Giải sbt Lịch sử 6 – Chân trời sáng tạo
- Lý thuyết Lịch sử lớp 6 – Chân trời sáng tạo
- Giải sgk GDCD 6 – Chân trời sáng tạo
- Giải sbt GDCD 6 – Chân trời sáng tạo
- Lý thuyết GDCD 6 – Chân trời sáng tạo
- Giải sgk Công nghệ 6 – Chân trời sáng tạo
- Giải sbt Công nghệ 6 – Chân trời sáng tạo
- Lý thuyết Công nghệ 6 – Chân trời sáng tạo
- Giải sgk Khoa học tự nhiên 6 – Chân trời sáng tạo
- Giải sbt Khoa học tự nhiên 6 – Chân trời sáng tạo
- Lý thuyết Khoa học tự nhiên 6 – Chân trời sáng tạo
- Giải sgk Tiếng Anh 6 - Friends plus
- Trọn bộ Từ vựng Tiếng Anh 6 Friends plus đầy đủ nhất
- Ngữ pháp Tiếng Anh 6 Friends plus
- Giải sbt Tiếng Anh 6 - Friends plus
- Bài tập Tiếng Anh 6 Friends plus theo Unit có đáp án