Lý thuyết Hình vuông, Tam giác đều, Lục giác đều – Toán lớp 6 Chân trời sáng tạo

A. Lý thuyết Toán 6 Bài 1: Hình vuông, Tam giác đều, Lục giác đều - Chân trời sáng tạo

1. Hình vuông

Hình vuông có:

+ Bốn đỉnh.

+ Bốn cạnh bằng nhau.

+ Bốn góc bằng nhau và bằng góc vuông.

+ Hai đường chéo của hình vuông bằng nhau.

Ví dụ:

Hình vuông ABCD có:

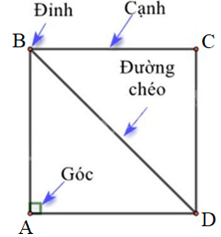
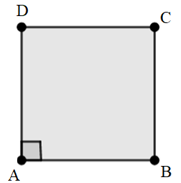
- Bốn đỉnh A, B, C, D.

- Bốn cạnh bằng nhau: AB = BC = CD = DA.

- Bốn góc ở các đỉnh A, B, C, D là góc vuông.

- Hai đường chéo bằng nhau: AC = BD.

Cách vẽ hình vuông

Vẽ bằng ê ke hình vuông ABCD, biết độ dài cạnh bằng a (cm).

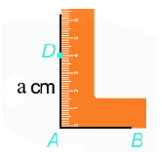
Bước 1: Vẽ đoạn thẳng AB = a (cm).

Bước 2: Vẽ đường thẳng vuông góc với AB tại A. Xác định điểm D trên đường thẳng đó sao cho AD = a (cm).

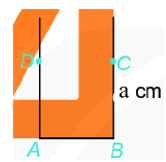
Bước 3: Vẽ đường thẳng vuông góc với AB tại B. Xác định điểm C trên đường thẳng đó sao cho BC = a (cm).

Bước 4: Nối C với D ta được hình vuông ABCD.

2. Tam giác đều

Tam giác đều có:

+ Ba đỉnh.

+ Ba cạnh bằng nhau.

+ Ba góc ở ba đỉnh bằng nhau.

Ví dụ:

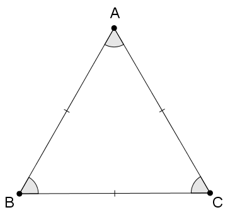
Tam giác đều ABC có:

- Ba đỉnh A, B, C.

- Ba cạnh bằng nhau: AB = BC = CA.

- Ba góc đỉnh A, B, C bằng nhau.

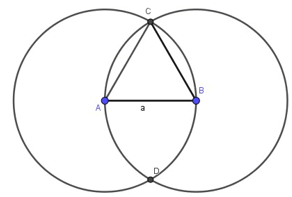
Cách vẽ tam giác đều

Cách vẽ tam giác đều cạnh a (cm) bằng thước và compa:

Bước 1: Dùng thước vẽ đoạn thẳng AB = a (cm).

Bước 2. Lấy A làm tâm, dùng compa vẽ một phần đường tròn có bán kính AB.

Bước 3: Lấy B làm tâm, dùng compa vẽ một phần đường tròn có bán kính BA; gọi C là giao điểm của hai phần đường tròn vừa vẽ.

Bước 4: Dùng thước vẽ các đoạn thẳng AC và BC.

Ta được tam giác ABC đều cạnh a (như hình vẽ).

3. Lục giác đều

Hình lục giác đều có sáu đỉnh, sáu cạnh bằng nhau, sáu góc ở các đỉnh bằng nhau, ba đường chéo chính bằng nhau.

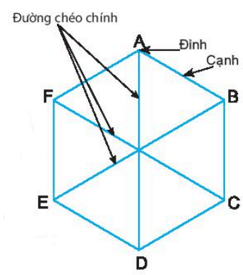
Ví dụ:

Lục giác đều ABCDEF có:

- Sáu đỉnh A, B, C, D, E, F.

- Sáu cạnh bằng nhau: AB = BC = CD = DE = EF.

- Sáu góc đỉnh A, B, C, D, E, F bằng nhau.

- Ba đường chéo chính bằng nhau AD = BE = CF.

Bài tập tự luyện

Bài 1. Dùng thước và êke để vẽ hình vuông cạnh 8 cm. Kẻ thêm hai đường chéo rồi dùng compa đo và so sánh độ dài của chúng.

Hướng dẫn giải

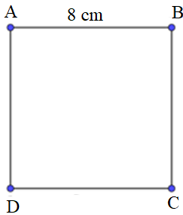
* Vẽ hình vuông cạnh 8 cm.

- Vẽ cạnh AB = 8 cm.

- Vẽ đường thẳng qua A vuông góc với AB. Trên đường thẳng này lấy điểm D sao cho AD = 8 cm.

- Vẽ đường thẳng qua B vuông góc với AB. Trên đường thẳng này lấy điểm C sao cho BC = 7cm.

- Nối C với D ta được hình vuông ABCD.

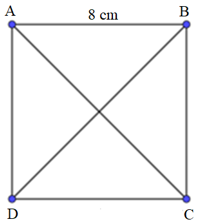
* Đo và so sánh độ dài hai đường chéo của hình vuông ABCD.

- Nối A với C, B với D. Khi đó, AC và BD là hai đường chéo của hình vuông ABCD.

- Mở compa một đoạn bằng AC và giữ nguyên compa.

- Đặt một đầu của compa trùng với một trong hai điểm của đoạn thẳng BD, ta thấy điểm còn lại trùng với đầu kia của compa.

Do đó hai đường chéo của hình vuông ABCD bằng nhau.

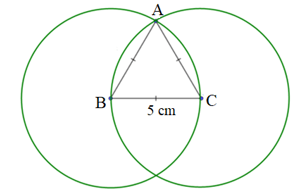
Bài 2. Dùng thước và compa để vẽ hình tam giác đều cạnh 5 cm.

Hướng dẫn giải

Bước 1: Vẽ đoạn thẳng BC = 5 cm.

Bước 2: Vẽ đường tròn tâm C bán kính 5 cm và đường tròn tâm B bán kính 5 cm. 

Bước 3: Gọi A là một trong hai giao điểm của đường tròn. 

Khi đó ta có: AB = AC = BC = 5 cm, các góc của tam giác ABC bằng nhau.

Ta được tam giác đều ABC cạnh 5 cm.

B. Trắc nghiệm Hình vuông, Tam giác đều, Lục giác đều (Chân trời sáng tạo 2023) có đáp án

Câu 1.

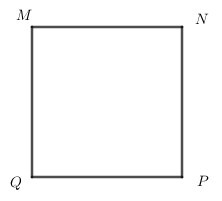
Cho hình vuông MNPQ, khẳng định nào sau đây đúng?

A. MN và PQ song song

B. MN và NP song song

C. MQ và PQ song song

D. MN và MQ song song

Hiển thị đáp án  

Đáp án: A

Giải thích:

Câu 2. Chọn phát biểu sai?

A. Hình vuông có bốn cạnh bằng nhau

B. Hình vuông có bốn cặp cạnh đối song song

C. Hình vuông có hai đường chéo bằng nhau

D. Hình vuông có bốn góc bằng nhau

Hiển thị đáp án  

Đáp án: B

Giải thích:

Hình vuông có hai cặp cạnh đối song song => Đáp án B sai.

Câu 3. Phát biểu nào sau đây sai?

A. Hình lục giác đều có 6 đỉnh

B. Hình lục giác đều có 6 cạnh

C. Hình lục giác đều có 6 đường chéo chính

D. Hình lục giác đều có 6 góc

Hiển thị đáp án  

Đáp án: C

Giải thích:

Các đáp án A, B, D đúng.

Hình lục giác đều có 3 đường chéo chính => Đáp án C sai.

Câu 4.

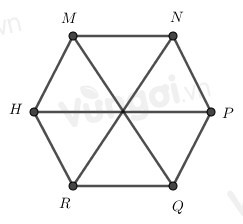
Cho hình lục giác đều MNPQRH, phát biểu nào sai?

A. MQ = NR

B. MH = RQ

C. MN = HR

D. MH = MQ

Hiển thị đáp án  

Đáp án: D

Giải thích:

Hình lục giác đều MNPQRH có 3 đường chéo chính bằng nhau nên: MQ = NR

=> A đúng

Hình lục giác đều MNPQRH có 6 cạnh bằng nhau nên MH = RQ và MN = HR

=> B, C đúng

Do MH là cạnh, MQ là đường chéo chính nên hai đoạn này không bằng nhau

=> D sai

Câu 5. Cho hình lục giác đều MNPQRH, có bao nhiêu tam giác đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều

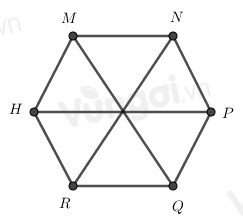
A. 8

B. 2

C. 4

D. 6

Hiển thị đáp án  

Đáp án: D

Giải thích:

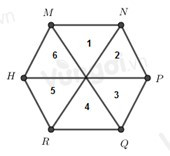
Ta đánh số như hình trên

Nhận thấy có các hình tam giác đều là: 1, 2, 3, 4, 5, 6.

Vậy có 6 tam giác đều.

Câu 6.

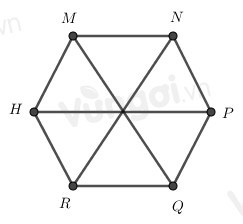
Cho hình lục giác đều MNPQRH, phát biểu nào sai?

A. 6 đỉnh là M, N, P, Q, R, H

B. 6 cạnh là MN, NP, PQ, MQ, QR, HM

C. 3 đường chéo chính là MQ, HP, RN

D. 3 đường chéo chính cắt nhau tại 1 điểm

Hiển thị đáp án  

Đáp án: B

Giải thích:

Đáp án B sai do MQ là đường chéo chính, sửa lại:

6 cạnh là MN, NP, PQ, HR, QR, HM

Câu 7. Chọn phát biểu sai:

A. Tam giác đều có ba cạnh

B. Ba cạnh của tam giác đều bằng nhau

C. Bốn góc của tam giác đều bằng nhau

D. Tam giác đều có ba đỉnh

Hiển thị đáp án  

Đáp án: C

Giải thích:

Trong tam giác đều ba góc bằng nhau  =>  Đáp án C sai.

Câu 8. Cho tam giác đều MNP có MN = 5cm, khẳng định nào sau đây đúng?

A. NP = 3cm

B. MP = 4cm

C. NP = 6cm

D. MP = 5cm

Hiển thị đáp án  

Đáp án: D

Giải thích:

Trong tam giác đều ba cạnh bằng nhau mà MN = 5cm nên ta có: MN = NP = MP = 5cm

=> Chọn D

Câu 9. Hình dưới đây có mấy hình tam giác?

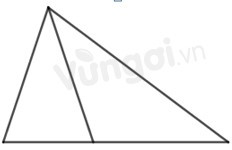
A. 1

B. 2

C. 3

D. 4

Hiển thị đáp án  

Đáp án: C

Giải thích:

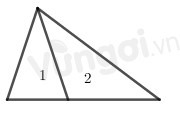
Hình trên có 2 hình tam giác nhỏ là: 1, 2 và 1 hình tam giác lớn ghép từ hai hình trên.

=> Có tất cả 3 hình tam giác.

Câu 10. Cho hình vuông MNPQ, khẳng định nào sau đây sai?

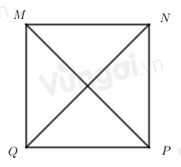
A. MN = PQ

B. MQ = QP

C. MN = NP

D. MN = MP

Hiển thị đáp án  

Đáp án: D

Giải thích:

Hình vuông MNPQ có: MN = NP = PQ = MQ

=> Đáp án A, B, C đúng.

Đáp án D sai do MN là cạnh của hình vuông, MP là đường chéo nên MN = MP là sai.

Xem thêm tóm tắt lý thuyết Toán lớp 6 sách Chân trời sáng tạo hay, chi tiết khác: