Lý thuyết Bội chung, Bội chung nhỏ nhất – Toán lớp 6 Chân trời sáng tạo

A. Lý thuyết Toán 6 Bài 12: Bội chung, Bội chung nhỏ nhất - Chân trời sáng tạo

1. Bội chung

Một số được gọi là bội chung của hai hay nhiều số nếu nó là bội của tất cả các số đó.

Ví dụ: Ta có: B(9) = {0; 9; 18; 27; 36; 45; 54; 63; 72; …};

B(12) = {0; 12; 24; 36; 48; 60; 72; …}.

Hai tập hợp này có một số phần tử chung như 0; 36; 72; … Ta nói chúng là các bội chung của 9 và 12.

• Kí hiệu tập hợp các bội chung của a và b là BC(a, b).

• Tương tự, tập hợp các bội chung của a, b, c là BC(a, b, c).

Ví dụ:

- Tập hợp các bội chung của 15 và 55 là BC(15, 55).

- Tập hợp các bội chung của 16; 20; 25 là BC(16, 20, 25).

Cách tìm bội chung của hai số a và b:

- Viết tập hợp B(a) và bội B(b).

- Tìm những phần tử chung của B(a) và B(b).

Ví dụ:

Ta có: B(2) = {0; 2; 4; 6; 8; 10; 12; ...}

B(3) = {0; 3; 6; 9; 12; ...}

Những phần tử chung của B(2) và B(3) là 0; 6; 12; ...

Do đó BC(2, 3) = {0; 6; 12; ...}.

2. Bội chung nhỏ nhất

Bội chung nhỏ nhất của hai hay nhiều số là số nhỏ nhất khác 0 trong tập hợp các bội chung của các số đó.

Kí hiệu bội chung nhỏ nhất của a và b là BCNN(a, b).

Tương tự, bội chung nhỏ nhất của a, b và c là BCNN(a, b, c).

Nhận xét: Tất cả các bội chung của a và b đều là bội của BCN(a, b). Mọi số tự nhiên đều là bội của 1.

Do đó, với mọi số tự nhiên a và b (khác 0) ta có:

BCNN(a, 1) = a;

BCNN(a, b, 1) = BCNN(a, b).

Ví dụ:

• Ta có: BC(6, 8) = {0; 24; 48; 72; …} vì 24 là số nhỏ nhất khác 0 trong số các bội chung của 6 và 8, nên BCNN(6, 8) = 24.

Tất cả các bội chung của 6 và 8 (là 0; 24; 48; 72; …) đều là bội của BCNN(6, 8) là 24.

• BCNN(8, 1) = 1;

• BCNN(6, 8, 1) = BCNN(6, 8) = 24.

3. Tìm bội chung nhỏ nhất bằng cách phân tích các số ra thừa số nguyên tố

Quy tắc:

Muốn tìm BCNN của hai hay nhiều số lớn hơn 1, ta thực hiện theo ba bước sau:

Bước 1: Phân tích mỗi số ra thừa số nguyên tố.

Bước 2: Chọn ra các thừa số nguyên tố chung và riêng.

Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN phải tìm.

Ví dụ: Tìm BCNN của 15 và 20.

Hướng dẫn giải

Ta có: 15 = 3 . 5; 20 = 2² . 5.

Thừa số nguyên tố chung và riêng là 2; 3 và 5.

Số mũ lớn nhất của 2 là 2; của 3 là 1 và của 5 là 1.

Do đó BCNN(15, 20) = 2² . 3 . 5 = 60.

Chú ý:

• Nếu các số đã cho từng đôi một nguyên tố cùng nhau thì BCNN của chúng là tích của các số đó.

Ví dụ: 3 và 8; 8 và 11; 11 và 3 là các cặp đôi một nguyên tố cùng nhau.

Khi đó, BCNN(3, 8, 11) = 3 . 8 . 11 = 264.

• Trong các số đã cho, nếu số lớn nhất là bội của các số còn lại thì BCNN của các số đã cho chính là số lớn nhất ấy.

Ví dụ: Ta có BCNN(6, 12, 36) = 36 vì 36 ⋮ 9; 36 ⋮ 12 và 36 lớn hơn 9 và 12.

4. Ứng dụng trong quy đồng mẫu các phân số

Quy tắc:

Muốn quy đồng mẫu số nhiều phân số ta có thể làm như sau:

Bước 1: Tìm một bội chung của các mẫu số (thường là BCNN) để làm mẫu số chung.

Bước 2: Tìm thừa số phụ của mỗi mẫu số (bằng cách chia mẫu số chung cho từng mẫu số riêng).

Bước 3: Nhân tử số và mẫu số của mỗi phân số với thừa số phụ tương ứng.

Ví dụ: Quy đồng mẫu số hai phân số 7/30 và 5/42.

Hướng dẫn giải

Ta có: 30 = 2 . 3 . 5; 42 = 2 . 3 . 7.

Thừa số nguyên tố chung và riêng là 2; 3; 5 và 7.

Số mũ lớn nhất của 2; 3; 5 và 7 đều là 1.

Khi đó, BCNN(30, 42) = 2 . 3 . 5 . 7 = 210.

Do đó BC(30; 42) = {0; 210; 420; ...}

Cách 1: Chọn mẫu chung là 210. Ta được:

 .

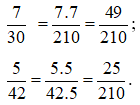
Cách 2: Chọn mẫu chung là một bội chung bất kì khác 0 của 30 và 42.

Chẳng hạn: chọn mẫu chung là 420, ta được:

 .

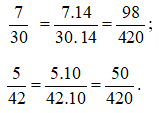
Bài tập tự luyện

Bài 1: Tìm:

a) BC(6, 14);

b) BC(6, 20, 30);

c) BCNN(10, 1, 12).

Hướng dẫn giải

a) Phân tích 6 và 14 ra thừa số nguyên tố, ta được:

6 = 2 . 3; 14 = 2 . 7.

Khi đó, BCNN(6, 14) = 2 . 3 . 7 = 42.

Do đó BC(6, 14) = {0; 42; 84; 126; …}.

Vậy BC(6, 14) = B(42) = {0; 42; 84; 126; …}.

b) Phân tích 6; 20 và 30 ra thừa số nguyên tố, ta được:

6 = 2 . 3; 20 = 2² . 5; 30 = 2 . 3 . 5.

Khi đó, BCNN(6, 20, 30) = 2² . 3 . 5 = 60.

Do đó BC(6, 20, 30) = B(60) = {0; 60; 120; 180; …}.

Vậy BC(6, 20, 30) = {0; 60; 120; 180; …}.

c) Ta có: BCNN(10, 1, 12) = BCNN(10, 12).

Phân tích 10 và 12 ra thừa số nguyên tố, ta được:

10 = 2 . 5; 12 = 2² . 3.

Khi đó BCNN(10, 12) = 2² . 3 . 5 = 60.

Vậy BCNN(10, 1, 12) = BCNN(10, 12) = 60.

Bài 2: Tìm số tự nhiên a nhỏ nhất khác 0, biết rằng a ⋮ 126, a ⋮ 198.

Hướng dẫn giải

Vì a ⋮ 126 và a ⋮ 198 nên a là BC(126, 198).

Vì a là số tự nhiên nhỏ nhất nên a $\in$ BCNN(126, 198).

Ta có: 126 = 2 . 3² . 7;

198 = 2 . 3² . 11.

Thừa số nguyên tố chung và riêng là 2; 3; 7 và 11.

Số mũ lớn nhất của 2 là 2, của 3 là 2, của là 7 và của 11 là 1.

BCNN(126, 198) = 2 . 3² . 7 . 11 = 1 386.

Vậy a = 1386.

Bài 3: Hai bạn Tùng và Hải thường đến thư viện đọc sách. Tùng cứ 8 ngày đến thư viện 1 lần, Hải 10 ngày 1 lần. Lần đầu cả hai bạn cùng đến thư viện vào một ngày. Hỏi ít nhất bao nhiêu ngày thì hai bạn cùng đến thư viện?

Hướng dẫn giải

Gọi a (ngày) là số ngày ít nhất hai bạn cùng đến thư viện ($�\in \mathrm{\mathbb{N}}$, x ≥ 10).

Số ngày ít nhất hai bạn cùng đến thư viện thuộc bội chung nhỏ nhất của 8 và 10.

Khi đó, a $\in$ BCNN(8, 10).

Ta có: 8 = 2³; 10 = 2 . 5

Do đó BCNN(8, 10) = 2³ . 5 = 40 (thỏa mãn điều kiện).

Vậy sau 40 ngày thì hai bạn cùng đến thư viện.

B. Trắc nghiệm Bội chung, Bội chung nhỏ nhất (Chân trời sáng tạo 2023) có đáp án

Câu 1. Số x là bội chung của a; b; c nếu:

A. x⋮a hoặc x⋮b hoặc x⋮c                

B. x⋮a và x⋮b

C. x⋮b và x⋮c       

D. x⋮a và x⋮b và x⋮c

Hiển thị đáp án  

Đáp án: D

Giải thích:

Số x là bội chung của 3 số a, b, c nếu x chia hết cho cả a, b, c.

Câu 2. Xác định số nhỏ nhất khác 0 trong các bội chung của 2 và 3.

A. 0

B. 6

C. 2

D. 3

Hiển thị đáp án  

Đáp án: B

Giải thích:

B(2) ={0;2;4;6;8;...}

B(3) ={0;3;6;9;...}

Số nhỏ nhất khác 0 trong bội chung của 2 và 3 là: 6.

Câu 3. Tìm BCNN(38,76)

A. 2888                         

B. 37                            

C. 76                          

D. 144

Hiển thị đáp án  

Đáp án: C

Giải thích:

Ta có 76⋮38 nên BCNN(38;76)=76.

Câu 4. Tìm bội chung nhỏ nhất của 9 và 15, biết 9 = 3²  và 15 = 3. 5.

A. 15

B. 45

C. 90

D. 150

Hiển thị đáp án  

Đáp án: B

Giải thích:

Thừa số nguyên tố của 9 là 3.

Thừa số nguyên tố của 15 là 3 và 5.

Các thừa số chung và riêng của 9 và 15 là 3 và 5.

Số mũ lớn nhất của 3 là 2, số mũ lớn nhất của 5 là 1.

BCNN(9, 15) = 3².5= 45.

Câu 5. Quy đồng mẫu hai phân số $\frac{7}{9}$ và $\frac{4}{15}$ với mẫu số nhỏ nhất thì được các phân số lần lượt là:

A. $\frac{12}{45}$ và $\frac{35}{45}$

B. $\frac{35}{45}$ và $\frac{12}{45}$

C. $\frac{70}{90}$ và $\frac{24}{90}$

D. $\frac{45}{35}$ và $\frac{12}{35}$

Hiển thị đáp án  

Đáp án: B

Giải thích:

Ta có: BCNN (9, 15) – 45 nên:

$\frac{7}{9}=\frac{7.5}{9.5}=\frac{35}{45}$ 

$\frac{4}{15}=\frac{4.3}{15.3}=\frac{12}{45}$

Câu 6. Mẫu số nhỏ nhất khi quy đồng các phân số $\frac{3}{16}$ và $\frac{5}{24}$ là

A. 24

B. 48

C. 96

D. 16

Hiển thị đáp án  

Đáp án: B

Giải thích:

Ta có: BCNN(16, 24) = 48

Mẫu chung nhỏ nhất khi quy đồng $\frac{3}{16}$ và $\frac{5}{24}$là 48.

Câu 7. Chọn câu trả lời sai.

A. 5∈ ƯC(55;110)

B. 24∈BC(3;4)          

C. 10∉ ƯC(55;110)            

D. 12⊂BC(3;4)

Hiển thị đáp án  

Đáp án: D

Giải thích:

+) Ta thấy 55⁝5; 110⁝5 nên 5ϵ ƯC(55;110)

Do đó A đúng.

+) Vì 24⁝3; 24⁝4 nên 24ϵBC(3;4)

 Do đó B đúng.

+) Vì 55 không chia hết cho 10 nên 10∉ ƯC(55;110)  

 Do đó C đúng.

+) Vì 12⁝3;12⁝4  nên 12ϵBC(3;4).  Kí hiệu 12⊂BC(3;4) là sai.

Do đó D sai.

Câu 8. Cho  a∈BC(6; 8), vậy số a nhận giá trị nào sau đây:

A. 2                               

B. 12                                 

C. 24                                        

D. 36

Hiển thị đáp án  

Đáp án: C

Giải thích:

B(6) ={0,6,12,24...}

B(8) ={0,8,24,...}

BC(6,8) ={0,24,...}

Câu 9. Giao của tập của hai tập hợp  A={toán, văn, thể dục, ca nhạc} và B={mỹ thuật, toán, văn, giáo dục công dân}

A. C ={toán, văn, thể dục}

B. C ={toán, văn}

C. C ={toán, văn, thể dục, ca nhạc}

D. C ={toán, thể dục, giáo dục công dân}

Hiển thị đáp án  

Đáp án: B

Giải thích:

Gọi C=A∩B

Vậy C={toán, văn}

Câu 10. BCNN(10, 15, 30) là:

A. 10

B. 15

C. 30

D. 60

Hiển thị đáp án  

Đáp án: C

Giải thích:

Ta có: 30 là bội của 10 và 15

=> BCNN(10, 15, 30) = 30.

Xem thêm tóm tắt lý thuyết Toán lớp 6 sách Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 8: Dấu hiệu chia hết cho 3, cho 9

Lý thuyết Bài 9: Ước và bội

Lý thuyết Bài 10: Số nguyên tố, Hợp số, Phân tích một số ra thừa số nguyên tố

Lý thuyết Bài 11: Ước chung, Ước chung lớn nhất

Lý thuyết Ôn tập Chương 1