Nội dung bài viết

    Xem thêm

    Lý thuyết Dấu hiệu chia hết cho 2, cho 5 – Toán lớp 6 Chân trời sáng tạo

    Với lý thuyết Toán lớp 6 Bài 7: Dấu hiệu chia hết cho 2, cho 5 chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sách Chân trời sáng tạo sẽ giúp học sinh nắm vững kiến thức trọng tâm để học tốt môn Toán 6.

    1 591 24/04/2023
    Trang trước
    Chia sẻ
    Trang sau  

    A. Lý thuyết Toán 6 Bài 7: Dấu hiệu chia hết cho 2, cho 5 - Chân trời sáng tạo

    1. Dấu hiệu chia hết cho 2

    Các số có chữ số tận cùng là 0; 2; 4; 6; 8 (tức là chữ số chẵn) thì chia hết cho 2 và chỉ những số đó mới chia hết cho 2.

    Ví dụ:

    a) Số 15 552 chia hết cho 2 vì có chữ số tận cùng là 2.

    b) Số 955 không chia hết cho 2 vì có chữ số tận cùng là 5 (5 không là số chẵn).

    2. Dấu hiệu chia hết cho 5

    Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.

    Ví dụ: Xét số 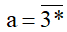Dấu hiệu chia hết cho 2, cho 5 | Lý thuyết Toán lớp 6 Chân trời sáng tạo . Thay * bởi số nào thì a chia hết cho 5, bởi số nào thì a không chia hết cho 5?

    Hướng dẫn giải

    Chữ số tận cùng của a là ∗ nên để a chia hết cho 5 thì ∗ phải là 0 hoặc 5.

    Để a không chia hết cho 5 thì ∗ phải khác 0 hoặc 5, tức là các số 1; 2; 3; 4; 6; 7; 8; 9.

    Vậy thay ∗ bằng 1; 2; 3; 4; 6; 7; 8; 9 thì a không chia hết cho 5.

    Bài tập tự luyện

    Bài 1. Từ ba số 2; 3; 7. Hãy ghép thành các số có ba chữ số khác nhau và chia hết cho 2.

    Hướng dẫn giải

    Số được ghép thành chia hết cho 2 nên phải có chữ số hàng đơn vị là 2.

    Hai chữ số hàng chục có thể là 3 hoặc 7.

    - Nếu chữ số hàng chục là 3 thì chữ số hàng trăm là 7.

    Ta được số cần tìm là 732.

    - Nếu chữ số hàng chục là 7 thì chữ số hàng trăm là 3.

    Ta được số cần tìm là 372.

    Vậy có hai số có thể ghép thành là 372 và 732.

    Bài 2. Tìm b để số 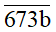Dấu hiệu chia hết cho 2, cho 5 | Lý thuyết Toán lớp 6 Chân trời sáng tạo  vừa chia hết cho 2 vừa chia hết cho 5?

    Hướng dẫn giải

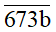
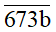
    Để Dấu hiệu chia hết cho 2, cho 5 | Lý thuyết Toán lớp 6 Chân trời sáng tạo  chia hết cho 2 thì b là số chẵn.

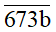
    Để Dấu hiệu chia hết cho 2, cho 5 | Lý thuyết Toán lớp 6 Chân trời sáng tạo chia hết cho 5 thì b là 0 hoặc 5.

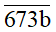
    Do đó để Dấu hiệu chia hết cho 2, cho 5 | Lý thuyết Toán lớp 6 Chân trời sáng tạo vừa chia hết cho 2 vừa chia hết cho 5 thì b = 0.

    Vậy để Dấu hiệu chia hết cho 2, cho 5 | Lý thuyết Toán lớp 6 Chân trời sáng tạo  vừa chia hết cho 2 vừa chia hết cho 5 thì b = 0.

    Bài 3. Có bao nhiêu số có hai chữ số chia hết cho 5.

    Hướng dẫn giải

    Các số có hai chữ số chia hết cho 5 là: 10; 15; 20; ….; 95.

    Số các số có hai chữ số chia hết cho 5 là:

    (95 – 10) : 5 + 1 = 18 (số)

    Vậy có 18 số có hai chữ số chia hết cho 5.

    B. Trắc nghiệm Dấu hiệu chia hết cho 2, cho 5 (Chân trời sáng tạo 2023) có đáp án

    Câu 1. Hãy chọn câu sai:

    A. Số chia hết cho 2 và 5 có tận cùng là số 0

    B. Một số chia hết cho 10 thì số đó chia hết cho 2

    C. Số chia hết cho 2 thì có tận cùng là số lẻ

    D. Số dư trong phép chia một số cho 2 bằng số dư trong phép chia chữ số tận cùng của nó cho 2

    Đáp án: C

    Giải thích:

    Số chia hết cho 2 có tận cùng là số chẵn nên câu sai là: Số chia hết cho 2 có tận cùng là số lẻ.

    Câu 2. Từ ba trong 4 số 5, 6, 3, 0, hãy ghép thành số có ba chữ số khác nhau là số lớn nhất chia hết cho 2 và 5.

    A. 560       

    B. 360

    C. 630 

    D. 650

    Đáp án: D

    Giải thích:

    Số chia hết cho 2  và 5 có tận cùng là 0  nên chữ số hàng đơn vị của các số này là 0.  

    Từ đó ta lập được các số có 3 chữ số khác nhau chia hết cho 2 và 5 là: 

    560; 530; 650; 630; 350; 360.

    Số lớn nhất trong 6 số trên là 650.

    Vậy số cần tìm là 650.

    Câu 3. Chọn câu trả lời đúng.

    Trong các số 2055; 6430; 5041; 2341; 2305

    A. Các số chia hết cho 5 là 2055; 6430; 5041

    B. Có hai số chia hết cho 3 là 2055 và 6430

    C. Các số chia hết cho 5 là 2055; 6430; 2305

    D. Không có số nào chia hết cho 3

    Đáp án: C

    Giải thích:

    Các số 2055; 6430; 2305 có tận cùng là 0 hoặc 5 nên các số đó chia hết cho 5. Suy ra C đúng, A sai.

    Chỉ có một số chia hết cho 3 là 2055 nên B, D sai.

    Câu 4. Số tự nhiên a chia cho 65 dư 10. Khi đó số tự nhiên a

    A. Chia cho 5 dư 1

    B. Chia cho 5 dư 4

    C. Chia cho 5 dư 3

    D. Chia hết cho 5

    Đáp án: D

    Giải thích:

    Vì số tự nhiên a chia cho 65 dư 10 nên ta có a = 65q + 10 (q∈N).

    Mà 65⁝5 và 10⁝5 nên a = 65q + 10chia hết cho 5.

    Câu 5. Cho 17*¯ chia hết cho 2. Số thay thế cho * có thể là

    A. 1

    B. 2

    C. 3

    D. 5

    Đáp án: B

    Giải thích:

    Vì * là chữ số tận cùng của 17*¯nên * chỉ có thể là 0; 2; 4; 6; 8.

    Vậy số 2 là số cần tìm.

    Câu 6. Các số có chữ số tận cùng là … thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.

    A. 0, 1, 2, 3

    B. 0, 2, 4, 6, 8

    C. 1, 3, 5, 7, 9

    D. 0 hoặc 5

    Đáp án: D

    Giải thích:

    Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.

    Câu 7. Trong những số sau, có bao nhiêu số chia hết cho 2?

    100000984, 12345, 12543456, 1234567, 155498

    A. 2

    B. 3

    C. 4

    D. 5

    Đáp án: B

    Giải thích:

    Các số 100000984, 12543456, 155498 có chữ số tận cùng là số chẵn nên chia hết cho 2.

    Các số còn lại có chữ số tận cùng là số lẻ (5, 7) nên không chia hết cho 2.

    Vậy có 3 số chia hết cho 2.

    Câu 8. Tổng chia hết cho 5 là

    A. A = 5+15+70+1995

    B. B = 10+25+34+2000

    C. C = 25+15+33+45

    D. D = 15+25+1000+2007

    Đáp án: A

    Giải thích:

    Vì 5⁝5; 15⁝5; 70⁝5; 1995⁝5 nên A = (5+15+70+1995)⁝5

    Câu 9. Lớp 6A có 45 học sinh, có thể chia lớp thành hai nhóm, mỗi nhóm có số lượng học sinh bằng nhau.

    Đúng

    Sai

    Đáp án: 

    Giải thích:

    Để mỗi nhóm có số lượng học sinh bằng nhau thì 45 phải chia hết cho 2.

    Điều này không xảy ra vì chữ số tận cùng của 45 là 5 nên 45 không chia hết cho 2.

    Câu 10. Số lớn nhất có 4 chữ số khác nhau và chia hết cho 2 là:

    A. 9998

    B. 9876

    C. 1234

    D. 1023

    Đáp án: B

    Giải thích:

    Số lớn nhất có 4 chữ số khác nhau bắt đầu bằng chữ số 9. Hai chữ số tiếp theo là 8 và 7.

    Chữ số cuối cùng chia hết cho 2 và khác 8 nên là số 6.

    Vậy số lớn nhất có 4 chữ số khác nhau và chia hết cho 2 là: 9876

    Xem thêm tóm tắt lý thuyết Toán lớp 6 sách Chân trời sáng tạo hay, chi tiết khác:

    Lý thuyết Bài 5: Thứ tự thực hiện các phép tính

    Lý thuyết Bài 6: Chia hết và chia có dư, Tính chất chia hết của một tổng

    Lý thuyết Bài 8: Dấu hiệu chia hết cho 3, cho 9

    Lý thuyết Bài 9: Ước và bội

    Lý thuyết Bài 10: Số nguyên tố, Hợp số, Phân tích một số ra thừa số nguyên tố

    Tham khảo các loạt bài Toán 6 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 591 24/04/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: