ĐỀ THI THỬ THPT QUỐC GIA NĂM HỌC 2019 MÔN TOÁN
ĐỀ THI THỬ THPT QUỐC GIA NĂM HỌC 2019 MÔN TOÁN (Đề số 17)
-
5234 lượt thi
-
50 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 5:
05/11/2024Mặt cầu có tâm O và tiếp xúc với mặt phẳng (P): x + 2y - 2z - 6 = 0 có phương trình là
 Xem đáp án
Xem đáp án
Đáp án đúng: D
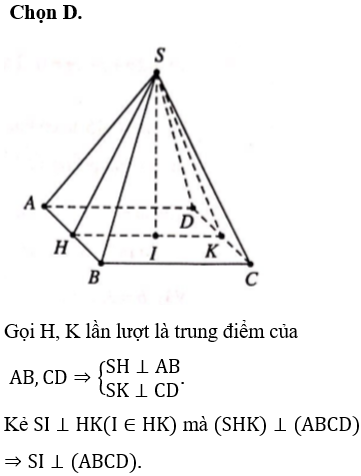
*Lời giải:

*Phương pháp giải:
- tính ra bán kính của mặt cầu: Do mặt cầu tiếp xúc mặt phẳng nên bán kính mặt cầu = d(mặt cầu, mặt phẳng)
- Do tâm O (0,0,0) nên phương trình mặt cầu có dạng:
x2 + y2 + z2 = R2
*Lý thuyến cần nắm và dạng bài toán về phương trình mặt cầu:
Trong không gian Oxyz, mặt cầu (S) tâm I (a; b; c) và bán kính R có phương trình là
(S):(x−a)2+(y−b)2+(z−c)2=R2(1).
Phương trình mặt cầu nói trên có thể viết dưới dạng
(S):x2+y2+z2+2ax+2by+2cz+d=0 (2) với d=a2+b2+c2−R2
Từ đó ta có phương trình (2) với điều kiện a2+b2+c2−d>0 là phương trình mặt cầu tâm I (-a; -b; -c) có bán kính là R=√a2+b2+c2−d
Đặc biệt nếu mặt cầu (S) có {tâm O(0;0;0)bán kính R thì phương trình mặt cầu (S) là
(S): x2+y2+z2=R2
Các dạng bài tập và cách viết phương trình mặt cầu
Dạng 1: Xác định tâm và bán kính mặt cầu – Điều kiện để (S) là một mặt cầu
Phương pháp giải:
Xét phương trình :
(S):(x−a)2+(y−b)2+(z−c)2=R2
Khi đó mặt cầu có tâm I (a; b; c), bán kính R
+) Xét phương trình :
(S):x2+y2+z2−2ax−2by−2cz+d=0
Khi đó mặt cầu có:
{tâm I(a;b;c)bán kính R=√a2+b2+c2−d
Điều kiện để (S) là phương trình mặt cầu là a2+b2+c2−d>0
+) Đặc biệt: (S): x2+y2+z2=R2, suy ra (S) có {tâm O(0;0;0)bán kính R
Dạng 2: Viết phương trình mặt cầu khi biết tâm và bán kính
Phương pháp giải:
Bước 1: Xác định tâm I (a; b; c).
Bước 2: Xác định bán kính R của (S).
Bước 3: Thế vào phương trình (S):
Dạng phương trình mặt cầu (S) có tâm I (a; b; c) và bán kính R.
(S): (x−a)2+(y−b)2+(z−c)2=R2
Dạng 3: Viết phương trình mặt cầu biết tâm và tiếp xúc với mặt phẳng
Phương pháp giải:
Cho điểm I (a; b; c) và mặt phẳng (P): Ax + By + Cz + D = 0
Vì mặt cầu tiếp xúc với mặt phẳng nên ta có
R=d(I;(P))=|Aa+Bb+Cc+D|√A2+B2+C2
Từ đó viết được phương trình mặt cầu tâm I và bán kính R đã tính phía trên.
Dạng 4: Viết phương trình mặt cầu biết tâm và tiếp xúc với đường thẳng
Phương pháp giải:
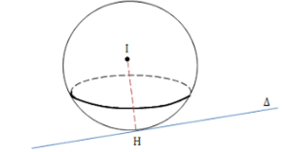
Cho điểm I (a; b; c) và đường thẳng d.
Gọi H là tiếp điểm của đường thẳng d và mặt cầu tâm I. Tìm H.
Khi đó bán kính của mặt cầu R = IH.
Xem thêm các bài viết liên quan hay, chi tiết
Phương trình mặt cầu (lý thuyết và cách giải các dạng bài tập)
Toán 12 Bài 17 (Kết nối tri thức): Phương trình mặt cầu
Câu 30:
25/11/2024Chọn ngẫu nhiên một số nguyên dương nhỏ hơn 21. Xác suất để số được chọn là số chia hết cho 3 bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Lời giải

*Phương pháp giải:
1.Tính số phần tử của không gian mẫu
2Liệt kê những phần tử của biến cố
3.Tính xác suất
*Lý thuyết:
a) Công thức cộng xác suất
- Nếu A ∩ B = ∅ thì A và B được gọi là hai biến cố xung khắc.
- Nếu hai biến cố A, B xung khắc nhau thì P(A ∪ B) = P(A) + P(B)
- Nếu các biến cố A1 ; A2; A3 ; … An đôi một xung khắc với nhau thì
P(A1 ∪ A2 ∪ ...∪ AK ) = P(A1) + P(A2) +... + P(AK)
- Công thức tính xác suất của biến cố đối: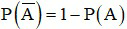
- Mở rộng: Với hai biến cố bất kì cùng liên quan đến phép thử thì:
P(A ∪ B) = P(A) + P(B) − P(A ∩ B)
b) Công thức nhân xác suất
- Hai biến cố gọi là độc lập nếu việc xảy ra hay không xảy ra của biến cố này không ảnh hưởng tới xác suất xảy ra biến cố kia.
- Nếu A và B là hai biến cố độc lập khi và chỉ khi P(A ∩ B) = P(A). P(B)
- Một cách tổng quát, nếu k biến cố A1,A2,A3,...,Ak là độc lập thì
P(A1 ∩ A2 ∩ A3 ∩...∩ AK ) = P(A1).P(A2).P(A3)...P(AK)
* Chú ý:
Nếu A và B độc lập thì A và 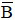
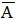
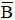
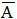
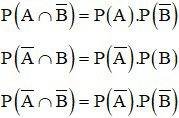
Xem thêm
Lý thuyết Xác suất lí thuyết và xác suất thực nghiệm – Toán lớp 8 Chân trời sáng tạo
Bài thi liên quan
-
ĐỀ THI THỬ THPT QUỐC GIA NĂM HỌC 2019 MÔN TOÁN (Đề số 01)
-
50 câu hỏi
-
60 phút
-
-
ĐỀ THI THỬ THPT QUỐC GIA NĂM HỌC 2019 MÔN TOÁN (Đề số 02)
-
50 câu hỏi
-
60 phút
-
-
ĐỀ THI THỬ THPT QUỐC GIA NĂM HỌC 2019 MÔN TOÁN (Đề số 03)
-
50 câu hỏi
-
60 phút
-
-
ĐỀ THI THỬ THPT QUỐC GIA NĂM HỌC 2019 MÔN TOÁN (Đề số 04)
-
50 câu hỏi
-
60 phút
-
-
ĐỀ THI THỬ THPT QUỐC GIA NĂM HỌC 2019 MÔN TOÁN (Đề số 05)
-
50 câu hỏi
-
60 phút
-
-
ĐỀ THI THỬ THPT QUỐC GIA NĂM HỌC 2019 MÔN TOÁN (Đề số 06)
-
50 câu hỏi
-
60 phút
-
-
ĐỀ THI THỬ THPT QUỐC GIA NĂM HỌC 2019 MÔN TOÁN (Đề số 07)
-
50 câu hỏi
-
60 phút
-
-
ĐỀ THI THỬ THPT QUỐC GIA NĂM HỌC 2019 MÔN TOÁN (Đề số 08)
-
50 câu hỏi
-
60 phút
-
-
ĐỀ THI THỬ THPT QUỐC GIA NĂM HỌC 2019 MÔN TOÁN (Đề số 09)
-
50 câu hỏi
-
60 phút
-
-
ĐỀ THI THỬ THPT QUỐC GIA NĂM HỌC 2019 MÔN TOÁN (Đề số 10)
-
50 câu hỏi
-
60 phút
-