Câu hỏi:
05/11/2024 1,533Mặt cầu có tâm O và tiếp xúc với mặt phẳng (P): x + 2y - 2z - 6 = 0 có phương trình là
A. .
B. .
C..
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: D
*Lời giải:

*Phương pháp giải:
- tính ra bán kính của mặt cầu: Do mặt cầu tiếp xúc mặt phẳng nên bán kính mặt cầu = d(mặt cầu, mặt phẳng)
- Do tâm O (0,0,0) nên phương trình mặt cầu có dạng:
x2 + y2 + z2 = R2
*Lý thuyến cần nắm và dạng bài toán về phương trình mặt cầu:
Trong không gian Oxyz, mặt cầu (S) tâm I (a; b; c) và bán kính R có phương trình là
(1).
Phương trình mặt cầu nói trên có thể viết dưới dạng
(2) với
Từ đó ta có phương trình (2) với điều kiện là phương trình mặt cầu tâm I (-a; -b; -c) có bán kính là
Đặc biệt nếu mặt cầu (S) có thì phương trình mặt cầu (S) là
Các dạng bài tập và cách viết phương trình mặt cầu
Dạng 1: Xác định tâm và bán kính mặt cầu – Điều kiện để (S) là một mặt cầu
Phương pháp giải:
Xét phương trình :
Khi đó mặt cầu có tâm I (a; b; c), bán kính R
+) Xét phương trình :
Khi đó mặt cầu có:
Điều kiện để (S) là phương trình mặt cầu là
+) Đặc biệt: , suy ra (S) có
Dạng 2: Viết phương trình mặt cầu khi biết tâm và bán kính
Phương pháp giải:
Bước 1: Xác định tâm I (a; b; c).
Bước 2: Xác định bán kính R của (S).
Bước 3: Thế vào phương trình (S):
Dạng phương trình mặt cầu (S) có tâm I (a; b; c) và bán kính R.
Dạng 3: Viết phương trình mặt cầu biết tâm và tiếp xúc với mặt phẳng
Phương pháp giải:
Cho điểm I (a; b; c) và mặt phẳng (P): Ax + By + Cz + D = 0
Vì mặt cầu tiếp xúc với mặt phẳng nên ta có
Từ đó viết được phương trình mặt cầu tâm I và bán kính R đã tính phía trên.
Dạng 4: Viết phương trình mặt cầu biết tâm và tiếp xúc với đường thẳng
Phương pháp giải:
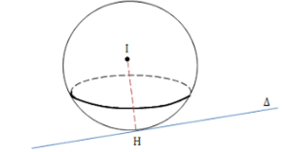
Cho điểm I (a; b; c) và đường thẳng d.
Gọi H là tiếp điểm của đường thẳng d và mặt cầu tâm I. Tìm H.
Khi đó bán kính của mặt cầu R = IH.
Xem thêm các bài viết liên quan hay, chi tiết
Phương trình mặt cầu (lý thuyết và cách giải các dạng bài tập)
Toán 12 Bài 17 (Kết nối tri thức): Phương trình mặt cầu
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AD = 2AB = 2CD = 2a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng (ABCD). Gọi M, N lần lượt là trung điểm của SB và CD (tham khảo hình vẽ bên). Tính sin góc giữa MN và (SAC), biết thể tích khối chóp S.ABCD bằng .
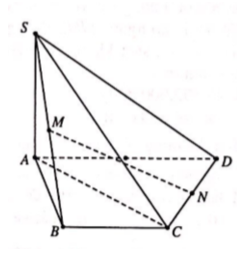
Câu 2:
Chọn ngẫu nhiên một số nguyên dương nhỏ hơn 21. Xác suất để số được chọn là số chia hết cho 3 bằng
Câu 3:
Cho hàm số có đồ thị như hình vẽ dưới đây. Số nghiệm của phương trình f(x) + 1 = 0 là
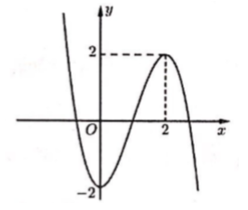
Câu 4:
Có 20 tấm thẻ được đánh số từ 1 đến 20. Chọn ngẫu nhiên 5 tấm thẻ. Xác suất trong 5 tấm được chọn có 3 tấm mang số lẻ, 3 tấm thẻ mang số chẵn trong đó có ít nhất một tấm thẻ mang số chia hết cho 4 là
Câu 5:
Trong không gian Oxyz, cho mặt cầu (S) có phương trình . Biết rằng mặt phẳng cắt (S) theo giao tuyến là đường tròn (C) có tâm là điểm P (a;b;c) và bán kính đường tròn (C) là r. Giá trị của tổng S = a + b + c + r là
Câu 6:
Trong không gian Oxyz, cho mặt cầu (S):. Mặt phẳng tiếp xúc (S) tại điểm P(-5;-4;6) là:
Câu 7:
Trong mặt phẳng tọa độ Oxy, gọi (H) là tập hợp điểm biểu diễn số phức thỏa mãn . Tính diện tích của hình (H).
Câu 8:
Cho các số phức z thỏa mãn . Biết rằng tập hợp điểm biểu diễn số phức w = iz + 1 - i là đường tròn. Tính bán kính của đường tròn đó.
Câu 9:
Cho hình chóp S.ABC có SA(ABC), tam giác ABC vuông cân tại B, AC = 2a và SA = a. Gọi M là trung điểm của SB. Tính thể tích khối chóp S.AMC.
Câu 10:
Hàm số f(x) liên tục trên [1;2018] và f(2018-x) = f(x), ∀x ∈ [1;2018], Tính
Câu 11:
Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số nghịch biến trên khoảng ?
Câu 12:
Biết rằng đồ thị hàm số và đồ thị hàm số cắt nhau tại hai điểm, kí hiệu là tọa độ hai điểm đó. Tính
Câu 13:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác đều, mặt bên SCD là tam giác vuông cân tại S. Gọi M là điểm thuộc đường thẳng CD sao cho BM vuống góc với SA. Tính thể tích V của khối chóp S.BDM?
Câu 14:
Trong không gian tọa độ Oxyz, cho hai điểm A(2;1;3), B(6;5;5). Gọi (S) là mặt cầu có đường kính AB. Mặt phẳng (P) vuông góc với đoạn AB tại H sao cho khối nón đỉnh A và đáy là hình tròn tâm H (giao của mặt cầu (S) và mặt phẳng (P) có thể tích lớn nhất, biết rằng (P): 2x + by + cz + d = 0 với b, c, d ∈ Z. Tính S = b + c + d.
Câu 15:
Trong không gian Oxyz, cho điểm B(4;2;-3) và mặt phẳng (Q): -2x + 4y + z - 7 = 0. Gọi B' là điểm đối xứng với B qua mặt phẳng (Q). Tính khoẳng cách từ B' đến (Q).



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)