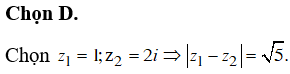50 câu hỏi trắc nghiệm thuộc ĐỀ THI THỬ THPT QUỐC GIA NĂM HỌC 2019 MÔN TOÁN (Đề số 19)

Mệnh đề nào dưới đây đúng?

A. Hàm số $y = \log_{\frac{1}{2}} x$ có tập xác định trên R

B. Hàm số $y = \log_{\frac{1}{2}} x$ nghịch biến trên khoảng $(0; + \infty)$

C. Hàm số $y = \log_{\frac{1}{2}} x$ đồng biến trên khoảng $(0; + \infty)$

D. Đồ thị hàm số $y = \log_{\frac{1}{2}} x$ luôn đi qua điểm (1,1)

Xem đáp án

Câu 2:

Cho hàm số $y = \frac{2 x + 1}{x + 1}$ có đồ thị (C). Mệnh đề nào dưới đây đúng?

A. (C) có tiệm cận đứng x = $- \frac{1}{2}$

B. (C) có tiệm cận đứng x = -1

C. (C) có tiệm cận đứng x = 2

D. (C) có tiệm cận đứng x = 1

Xem đáp án

Câu 3:

Tính thể tích V của khối lập phương ABCD.A' B' C' D' , biết AC'=a $\sqrt{3}$

A. V = 3 $\sqrt{3}$ $a^{3}$

B. V = 27 $a^{3}$

C. V = $a^{3}$

D. V = 3 $a^{3}$

Xem đáp án

Câu 4:

Cho tam giác ABC. Gọi M, N lần lượt là trung điểm các cạnh AB, AC. Mệnh đề nào sau đây là sai?

A. $\vec{AN} = \vec{NC}$

B. $\vec{MN} = \frac{1}{2} \vec{BC}$

C. $|\vec{MA}| = |\vec{MB}|$

D. $\vec{BC} = 2 \vec{NM}$

Xem đáp án

Câu 5:

Dãy số nào dưới đây có giới hạn bằng 0?

A. $(1, 01)^{n}$

B. ${(\frac{\sqrt{5}}{2})}^{n}$

C. ${(\frac{1}{3})}^{n}$ .

D. ${(\frac{5}{3})}^{n}$

Xem đáp án

Câu 6:

Biết rằng phương trình $z^{2} + bz + c = 0$ (b,c∈R) có một nghiệm phức là z = 1 + 2i. Khẳng định nào sau đây là đúng?

A. b + c = 0.

B. b + c = 2.

C. b + c = 3.

D. b + c = 7.

Xem đáp án

Câu 7:

Tìm giá trị cực đại của tham số m để hàm số $f (x) = \{\begin{cases} x + 1 khi x > 2 \\ x^{2} + m khi x \leq 2 \end{cases}$ liên tục tại điểm x = 2?

A. m = -1.

B. m = 0.

C. m = 3.

D. m = -6.

Xem đáp án

Câu 8:

Cho hàm số y = f(x) có bảng biến thiên như hình vẽ bên dưới.

Hàm số y = f(x) đồng biến trên khoảng nào sau đây?

A. (-2;2).

B. (0;2).

C. $(3; + \infty) .$

D. $(- \infty; 1) .$

Xem đáp án

Câu 9:

Hàm số bậc hai nào sau đây có đồ thị đi qua 3 điểm A(0;-2), B(1;2) ,C(-1;-4) ?

A. $y = x^{2} - 4 x + 3 .$

B. $y = - 2 x^{2} + 6 x - 2 .$

C. $y = - 3 x^{2} + x - 2 .$

D. $y = x^{2} + 3 x - 2 .$

Xem đáp án

Câu 10:

Trong không gian Oxyz, điểm M' đối xứng với điểm M(1;2;4) qua mặt phẳng $(α)$ : 2x + y + 2z - 3 = 0 có tọa độ là

A. (-3;0;0)

B. (-1;1;2)

C. (-1;-2;-4)

D. (2;1;2)

Xem đáp án

Câu 11:

Cho biết có hai số phức z thỏa mãn $z^{2} = 119 - 120 i$ , ký hiệu $z_{1} và z_{2}$ . Tính $| z_{1} - z_{2} |^{2} .$

A. 169.

B. 114244.

C. 338.

D. 676.

Xem đáp án

Câu 12:

Xét bất phương trình $5^{2} x - 3 . 5^{x + 2} + 32 < 0$ . Nếu đặt $t = 5^{x}$ thì phương trình trở thành bất phương trình nào sau đây?

A. $t^{2} - 3 t + 32 < 0 .$

B. $t^{2} - 16 t + 32 < 0 .$

C. $t^{2} - 6 t + 32 < 0 .$

D. $t^{2} - 75 t + 32 < 0 .$

Xem đáp án

Câu 13:

Trong không gian Oxyz, mặt cầu tâm I(1;2;3) cắt mặt phẳng $(α)$ : 2x - y - 2z + 18 = 0 theo một đường tròn có chu vi bằng $10 π$ có phương trình là:

A. $(x - 1)^{2} + (y - 2)^{2} + (z - 3)^{2} = 16$

B. $(x - 1)^{2} + (y - 2)^{2} + (z - 3)^{2} = 25$

C. $(x - 1)^{2} + (y - 2)^{2} + (z - 3)^{2} = 41$

D. $(x - 1)^{2} + (y - 2)^{2} + (z - 3)^{2} = 9$

Xem đáp án

Câu 14:

Cho tứ diện ABCD có các cạnh OA, OB, OC đôi một vuông góc và OA = OB = OC = 1. Khoảng cách giữa hai đường thẳng OA và BC bằng

A. $\frac{\sqrt{3}}{2}$

B. $\frac{\sqrt{2}}{2}$

C. $\frac{1}{\sqrt{3}}$

D. $\frac{1}{2}$

Xem đáp án

Câu 15:

Cho tam giác ABC vuông tại A và góc $\hat{ABC} = 30^{0}$ . Xác định góc giữa hai vectơ $(\vec{CA}; \vec{CB})$ .

A. $60^{0}$

B. $120^{0} .$

C. $- 30^{0} .$

D. $30^{0} .$

Xem đáp án

Câu 16:

Cấp số cộng $(u_{n})$ thỏa mãn $\{\begin{cases} u_{4} = 10 \\ u_{4} + u_{6} = 26 \end{cases}$ có công sai là

A. d = -3

B. d = 3

C. d = 5

D. d = 6

Xem đáp án

Câu 17:

Cho hình chữ nhật ABCD có diện tích bằng 24 và AB= $\frac{2}{3}$ BC. Thể tích khối tròn xoay có được khi quay hình chữ nhật ABCD quanh cạnh BC bằng

A. 96 $π$ .

B. 64 $π$ .

C. 144 $π$ .

D. 112 $π$

Xem đáp án

Câu 18:

Trên mặt phẳng tọa độ, tập hợp các điểm biểu diễn các số phức z thỏa mãn $| z - (3 - 4 i) | = 2$ là

A. Đường tròn tâm I(3;4), bán kính R = 2.

B. Đường tròn tâm I(-3;-4), bán kính R = 2.

C. Đường tròn tâm I(3;-4), bán kính R = 2.

D. Đường tròn tâm I(-3;4), bán kính R = 2

Xem đáp án

Câu 19:

Hàm số y = f(x) xác định và có đạo hàm trên R\{-1;1} có bảng biến thiên như hình bên. Đồ thị hàm số y = f(x) có tất cả bao nhiêu đường tiệm cận (đứng và ngang)?

A. 2

B. 3

C. 4

D. 5.

Xem đáp án

Câu 20:

Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng $(α) + x + 2 y - z - 1 = 0$ và $(β) : 2 x + 4 y - mz - 2 = 0$ . Tìm m để hai mặt phẳng $(α) và (β)$ song song với nhau.

A. m = 1.

B. Không tồn tại m.

C. m = -2.

D. m = 2.

Xem đáp án

Câu 21:

Biết rằng phương trình ${[\log_{\frac{1}{3}} (9 x)]}^{2} + \log_{3} \frac{x^{2}}{81} - 7 = 0$ có hai nghiệm phân biệt $x_{1}, x_{2}$ . Tính P $= x_{1} x_{2}$ .

A. $P = \frac{1}{9^{3}}$

B. $P = 3^{6} .$

C. $P = 9^{3} .$

D. $P = 3^{8}$

Xem đáp án

Câu 22:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: $\frac{x - 2}{1} = \frac{y - 2}{2} = \frac{z + 2}{- 1}$ và mặt phẳng $(α)$ : 2x + 2y - z - 4 = 0. Tam giác ABC có A(-1;2;1), các đỉnh B, C nằm trên (α) và trọng tâm G nằm trên đường thẳng d. Tọa độ trung điểm M của BC là

A. M(2;1;2)

B. M(0;1;-2)

C. M(1;-1;-4)

D. M(2;-1;-2)

Xem đáp án

Câu 23:

Cho dãy số $(u_{n})$ thỏa mãn $\log ({u_{1}}^{2} + {u_{2}}^{2} + 10) - \log (2 u_{1} + 6 u_{2}) = 0$ và $u_{n + 2} + u_{n} = 2 u_{n + 1} + 1$ với mọi n∈ N*. Giá trị nhỏ nhất của n để $u_{n}$ > 5050 bằng

A. 101.

B. 102.

C. 100.

D. 99.

Xem đáp án

Câu 24:

Cho hình chóp tứ giác đều S.ABCD, có đáy ABCD là hình vuông, cạnh bên bằng cạnh đáy và bằng a. Gọi M là trung điểm của SC. Góc giữa hai mặt phẳng (MBD) và (ABCD) bằng

A. $90^{0}$

B. $30^{0}$

C. $45^{0}$

D. $60^{0}$

Xem đáp án

Câu 25:

Một bảng khóa điện tử của phòng học gồm 10 nút, mỗi nút được ghi một số ừ 0 đến 9 và không có hai nút nào được ghi cùng một số. Để mở cửa cần nhấn liên tiếp 3 nút khác nhau sao cho 3 số trên 3 nút đó theo thứ tự đã nhẫn tạo thành một dãy số tăng và có tổng bằng 10. Một người không biết quy tắc mở cửa trên, đã nhấn ngẫu nhiên liên tiếp 3 nút khác nhau trên bảng điều khiển, tính xác suất để người đó mở được cửa phòng học.

A. $\frac{1}{12}$

B. $\frac{1}{72}$

C. $\frac{1}{90}$

D. $\frac{1}{15}$

Xem đáp án

Câu 26:

Trong không gian Oxyz, cho đường thẳng $Δ_{1} : \frac{x - 8}{2} = \frac{y + 2}{4} = \frac{z - 3}{m - 1}$ và $Δ_{2} : \{\begin{cases} y = 3 - t \\ \begin{matrix} z = 2 + 2 t \\ x = 4 + 4 t \end{matrix} \end{cases}$ . Giá trị của m để $Δ_{1} và Δ_{2}$ cắt nhau là

A. m = - $\frac{25}{8}$

B. m = $\frac{25}{8}$

C. m = 3.

D. m = -3

Xem đáp án

Câu 27:

Cho hàm số f(x) = $\frac{2 \sqrt{m} + m}{\sqrt{x} + 1}$ với m là tham số thực, m > 1. Gọi S là tập tất cả các giá trị nguyên dương của m để hàm số có giá trị lớn nhất trên đoạn [0;4] nhỏ hơn 3. Số phần tử của tập S là

A. 1

B. 3

C. 0

D. 2

Xem đáp án

Câu 28:

Cho hàm số y = f(x) là hàm lẻ, liên tục trên [-4;4], biết $\int_{- 2}^{0} f (- x) dx = 2$ và $\int_{1}^{2} f (- 2 x) dx = 4$ . Tính I= $2 \int_{0}^{4} f (x) dx$

A. I = -10.

B. I = -6.

C. I = 6.

D. I = 10

Xem đáp án

Câu 29:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = 3, BC = 4, đường thẳng SA vuông góc với mặt phẳng (ABC), SA = 4. Gọi AM, AN lần lượt là chiều cao của tam giác SAB và SAC. Thể tích khối tứ diện AMNC là

A. $\frac{128}{41}$

B. $\frac{768}{41}$

C. $\frac{384}{41}$

D. $\frac{256}{41}$

Xem đáp án

Câu 30:

Cho các số phức $z_{1}, z_{2}$ thỏa mãn $| z_{1} | = 1, | z_{2} | = 2$ và $z_{1} . \bar{z_{2}}$ là thuần ảo, tính $| z_{1} - z_{2} |$ .

A. $\sqrt{2}$ .

B. $\sqrt{3}$ .

C. 2

D. $\sqrt{5}$

Xem đáp án

Câu 31:

Cho (H) là hình phẳng giới hạn bởi parabol $y = \frac{1}{4} x^{2} + 1$ với $0 \leq x \leq 2 \sqrt{2}$ , nửa đường tròn $y = \sqrt{8 - x^{2}}$ và trục hoành, trục tung (phần tô đậm trong hình vẽ). Diện tích của (H) bằng

A. $\frac{3 π + 14}{6}$

B. $\frac{3 π + 2}{3}$

C. $\frac{3 π + 4}{3}$

D. c

Xem đáp án

Câu 32:

Cho hàm số y = f(x) liên tục trên R. Biết $\int_{0}^{x^{2}} f (t) dt = e^{x^{2}} + x^{4} - 1$ với ∀x ∈ R. Giá trị của f(4) là

A. $f (4) = e^{4} + 4 .$

B. $f (4) = e^{4}$

C. $f (4) = e^{4} + 8 .$

D. f(4)=1

Xem đáp án

Câu 33:

Cho ba số a, b, c, d theo thứ tự tạo thành cấp số nhân với công bội khác 1. Biết tổng ba số hạng đầu bằng $\frac{148}{9}$ , đồng thời theo thứ tự đó chúng lần lượt là số hạng thứ nhất, thứ tư và thứ tám của một cấp số cộng. Tính giá trị biểu thức T = a - b + c - d?

A. T = $\frac{101}{27}$

B. T = $\frac{100}{27}$

C. T = - $\frac{100}{27}$

D. T = - $\frac{101}{27}$

Xem đáp án

Câu 34:

Cho hình nón (N) có bán kính r = 20(cm), chiều cao h = 60(cm) và mọt hình trụ (T) nội tiếp hình nón (N) (hình trụ (T) có một đáy thuộc đáy hình nón và một đáy nằm trên mặt xung quanh của hình nón). Tính thể tích V của hình trụ (T) có diện tích xung quanh lớn nhất?

A. V=3000 $π ({cm}^{3})$ .

B. V= $\frac{32000}{9}$ $π ({cm}^{3})$ .

C. V=3600 $π ({cm}^{3})$ .

D. V=4000 $π ({cm}^{3})$ .

Xem đáp án

Câu 35:

Cho hàm số f(x) có đạo hàm không âm trên [0;1] thỏa mãn ( $\frac{[f (x)]^{2} [f' (x)]^{2})}{e^{2 x}} = 1 + [f (x)]^{2}$ và f(x) > 0 với ∀x ∈ [0;1], biết f(0) = 1. hãy chọn khẳng định đúng trong các khẳng định sau

A. $\frac{5}{2}$ < f(1) < 3

B. 3 < f(1) < $\frac{7}{2}$

C. 2 < f(1) < $\frac{5}{2}$

D. $\frac{3}{2}$ < f(1) < 2

Xem đáp án

Câu 36:

Trong không gian tọa độ Oxyz cho các điểm A(1;5;0), B(3;3;6) và đường thẳng Δ: $\frac{x + 1}{2} = \frac{y - 1}{- 1} = \frac{z}{2}$ . Gọi M(a;b;c) ∈ Δ sao cho chu vi tam giác MAB đạt giá trị nhỏ nhất. Tính tổng T = a + b + c?

A. T = 2.

B. T = 3

C. T = 4

D. T = 5

Xem đáp án

Câu 37:

Cho hàm số f(x) có đạo hàm liên tục trên R và thỏa mãn f(x) > 0, ∀x ∈ R. Biết f(0) = 1 và (2-x)f(x) - f'(x) = 0. Tìm tất cả các giá trị thực của tham số m để phương trình f(x) = m có hai nghiệm phân biệt.

A. m < $e^{2}$ .

B. 0 < m < $e^{2}$ .

C. 0 < m ≤ $e^{2}$ .

D. m > $e^{2}$

Xem đáp án

Câu 38:

Trong không gian với hệ tọa độ Oxyz, gọi (P) là mặt phẳng đi qua điểm M(4;1;1), cắt các tia Ox, Oy, Oz lần lượt tại A, B, C sao cho biểu thức OA + OB + OC đạt giá trị nhỏ nhất. Mặt phẳng (P) đi qua điểm nào dưới đây?

A. (2,0,2).

B. (2,2,0).

C. (2,1,1)

D. (0,2,2)

Xem đáp án

Câu 39:

Cho hàm số y = f(x) > 0 xác định và có đạo hàm trên đoạn [0;1] và thỏa mãn các điều kiện sau: g(x) = 1+2018 $\int_{0}^{x} f (t) dt; g (x) = f^{2} (x) .$ Tính $\int_{0}^{1} \sqrt{(g (x)} dx ?$

A. $\frac{1011}{2}$

B. $\frac{1009}{2}$

C. $\frac{2019}{2}$

D. 505

Xem đáp án

Câu 40:

Cho x, y là các số thực dương thay đổi. Xét hình chóp S.ABC có SA = x, BC = y, các cạnh còn lại đều bằng 1. Khi thể tích khối chóp S.ABC đạt giá trị lớn nhất thì tích x + y bằng:

A. $\frac{4}{3}$

B. $\frac{4 \sqrt{3}}{3}$

C. $2 \sqrt{3}$

D. $\frac{1}{3}$

Xem đáp án

Câu 41:

Chị Lan có 400 triệu đồng mang đi gửi tiết kiệm ở hai loại kì hạn khác nhau đều theo thể thức lãi kép. Chị gửi 200 triệu động theo kì hạn quý với lãi suất 2,1% một quý, 200 triệu đồng còn lại chị gửi theo kì hạn tháng với lãi suất 0,73% một tháng. Sau khi gửi được đúng 1 năm, chị rút ra một nửa số tiền ở loại kì hạn theo quý và gửi vào loại kì hạn theo tháng. Hỏi sau đúng 2 năm kể từ khi gửi tiền lần đầu, chị Lan thu được tất cả bao nhiêu tiền lãi (làm tròn đến hàng nghìn)?

A. 79760000.

B. 74813000

C. 65393000

D. 70656000.

Xem đáp án

Câu 42:

Cho hàm số y = f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y = f'(x) như hình vẽ bên. Xét hàm số g(x) = f(x²- 3) và các mệnh đề sau:

1. Hàm số g(x) có 3 điểm cực trị.

2. Hàm số g(x)đạt cực tiểu tại x = 0.

3. Hàm số g(x)đạt cực đại tại x = 2.

4. Hàm số g(x)đồng biến trên khoảng (-2;0).

5. Hàm số g(x)nghịch biến trên khoảng (-1;1).

Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?

A. 1.

B. 4.

C. 3.

D. 2.

Xem đáp án

Câu 43:

Trong không gian với hệ tọa độ Oxyz, cho điểm M thuộc mặt cầu (S): $(x - 3)^{2} + (y - 3)^{2} + (z - 2)^{2} = 9$ và ba điểm A(1;0;0); B(2;1;3); C(0;2;-3). Biết rằng quỹ tích các điểm M thỏa mãn ${MA}^{2} + 2 . \vec{MB} . \vec{MC} = 8$ là đường tròn cố định, tính bán kính r đường tròn này.

A. r = $\sqrt{3}$ .

B. r = 3.

C. r = $\sqrt{6}$

D. r = 6

Xem đáp án

Câu 44:

Cho dãy số $(u_{n})$ thỏa mãn $\log u_{5} - 2 {logu}_{2}$ $= 2 (1 + \sqrt{{logu}_{5} - 2 {logu}_{2} + 1})$ và $u_{n} = 3 u_{n - 1}$ ,∀ n ≥1. Giá trị lớn nhất của n để $u_{n} < 7^{100}$ bằng

A. 192

B. 191.

C. 179

D. 177.

Xem đáp án

Câu 45:

Cho z và w là hai số phức liên hợp thỏa mãn $\frac{z}{w^{2}}$ là số thực và $| z - w | = 2 \sqrt{3}$ . Mệnh đề nào sau đây là đúng?

A. 3 < $| z |$ < 4.

B. $| z |$ < 1.

C. 1 < $| z |$ < 3.

D. $| z |$ > 4.

Xem đáp án

Câu 46:

Phương trình mặt cầu (lý thuyết và cách giải các dạng bài tập)

Cho hàm số y = f(x). Hàm số y = f'(x) có đồ thị như hình bên.

Tìm m để hàm số $y = f (x^{2} + m)$ có 3 điểm cực trị?

A. $m \in [0; 3]$

B. $m \in [0; 3)$

C. $m \in (3; + \infty)$

D. $m \in (- \infty; 0)$

Xem đáp án

Câu 47:

06/11/2024

Trong không gian Oxyz cho mặt cầu (S): $(x - 1)^{2} + (y + 2)^{2} + (z - 3)^{2} = 27$ . Gọi $(α)$ là mặt phẳng đi qua hai điểm A(0;0;-4), B(2;0;0) và cắt (S) theo giao tuyến là đường tròn (C) sao cho khối nón có đỉnh là tâm của (S), đáy là (C) có thể tích lớn nhất. Biết mặt phẳng $(α)$ có phương trình dạng ax + by - z + c = 0, khi đó a - b + c bằng:

A. -4.

B. 8

C. 0

D. 2

Xem đáp án

Đáp án đúng: A

*Lời giải:

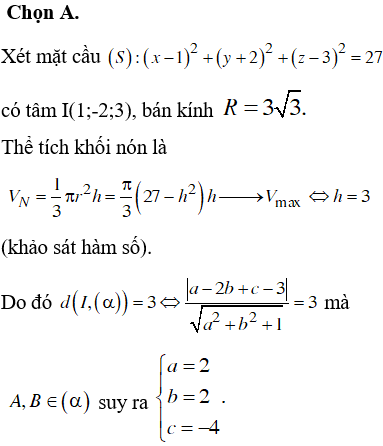
*Phương pháp giải:

- áp dụng phương trình mặt cầu tìm ra tâm I (-a,-b,-c) và bán kính R

- từ thể tích khối nón đạt giá trị max --> tính ra chiều cao h

*Cách giải và các dạng bài toán về phương trình mặt cầu và thể tích khối nón:

Trong không gian Oxyz, mặt cầu (S) tâm I (a; b; c) và bán kính R có phương trình là

$(S) : {(x - a)}^{2} + {(y - b)}^{2} + {(z - c)}^{2} = R^{2}$ (1).

Phương trình mặt cầu nói trên có thể viết dưới dạng

$(S) : x^{2} + y^{2} + z^{2} + 2 a x + 2 b y + 2 c z + d = 0$ (2) với $d = a^{2} + b^{2} + c^{2} - R^{2}$

Từ đó ta có phương trình (2) với điều kiện $a^{2} + b^{2} + c^{2} - d > 0$ là phương trình mặt cầu tâm I (-a; -b; -c) có bán kính là $R = \sqrt{a^{2} + b^{2} + c^{2} - d}$

Đặc biệt nếu mặt cầu (S) có $\{\begin{cases} tâm O (0; 0; 0) \\ bán kính R \end{cases}$ thì phương trình mặt cầu (S) là

$(S) : x^{2} + y^{2} + z^{2} = R^{2}$

Các dạng bài tập và cách viết phương trình mặt cầu

Dạng 1: Xác định tâm và bán kính mặt cầu – Điều kiện để (S) là một mặt cầu

Phương pháp giải:

Xét phương trình :

$(S) : {(x - a)}^{2} + {(y - b)}^{2} + {(z - c)}^{2} = R^{2}$

Khi đó mặt cầu có tâm I (a; b; c), bán kính R

+) Xét phương trình :

$(S) : x^{2} + y^{2} + z^{2} - 2 a x - 2 b y - 2 c z + d = 0$

Khi đó mặt cầu có:

$\{\begin{cases} tâm I (a; b; c) \\ bán kính R = \sqrt{a^{2} + b^{2} + c^{2} - d} \end{cases}$

Điều kiện để (S) là phương trình mặt cầu là $a^{2} + b^{2} + c^{2} - d > 0$

+) Đặc biệt: $(S) : x^{2} + y^{2} + z^{2} = R^{2}$ , suy ra (S) có $\{\begin{cases} tâm O (0; 0; 0) \\ bán kính R \end{cases}$

Dạng 2: Viết phương trình mặt cầu khi biết tâm và bán kính

Phương pháp giải:

Bước 1: Xác định tâm I (a; b; c).

Bước 2: Xác định bán kính R của (S).

Bước 3: Thế vào phương trình (S):

Dạng phương trình mặt cầu (S) có tâm I (a; b; c) và bán kính R.

$(S) : {(x - a)}^{2} + {(y - b)}^{2} + {(z - c)}^{2} = R^{2}$

Dạng 3: Viết phương trình mặt cầu biết tâm và tiếp xúc với mặt phẳng

Phương pháp giải:

Cho điểm I (a; b; c) và mặt phẳng (P): Ax + By + Cz + D = 0

Vì mặt cầu tiếp xúc với mặt phẳng nên ta có

$R = d (I; (P)) = \frac{| A a + B b + C c + D |}{\sqrt{A^{2} + B^{2} + C^{2}}}$

Từ đó viết được phương trình mặt cầu tâm I và bán kính R đã tính phía trên.

Dạng 4: Viết phương trình mặt cầu biết tâm và tiếp xúc với đường thẳng

Phương pháp giải:

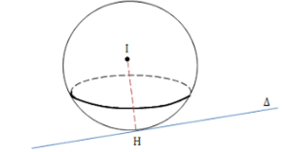
Cho điểm I (a; b; c) và đường thẳng d.

Gọi H là tiếp điểm của đường thẳng d và mặt cầu tâm I. Tìm H.

Khi đó bán kính của mặt cầu R = IH.

Công thức tính thể tích khối nón

Cho khối nón tròn xoay có diện tích đáy là S; chiều cao là h.

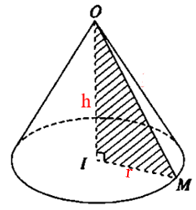
Khi đó : $V = \frac{1}{3} S . h = \frac{1}{3} π . r^{2} . h$

Xem thêm các bài viết liên quan hay, chi tiết

Toán 12 Bài 17 (Kết nối tri thức): Phương trình mặt cầu

Công thức tính thể tích khối nón chi tiết nhất – Toán 12

Câu 48:

Một hội nghị gồm 6 đại biểu nước A, 7 đại biểu nước B và 7 đại biểu nước C, trong đó mỗi nước có hai đại biểu là nữ. Chọn ngẫu nhiên ra 4 đại biểu, xác suất để chọn được 4 đại biểu để mỗi nước đều có ít nhất một đại biểu và có cả đại biểu nam và đại biểu nữ bằng

A. $\frac{46}{95}$

B. $\frac{3844}{4845}$

C. $\frac{49}{95}$

D. $\frac{1937}{4845}$

Xem đáp án

Chọn D.

Chọn ngẫu nhiên 4 đại biểu có: $C_{20}^{4}$ cách chọn.Chọn ra 4 đại biểu có đủ 3 nước dẫn đến 3 trường hợp:

1) 2A – 1B – 1C, 1A – 2B – 1C, 1A – 1B – 2C dẫn đến có $C_{6}^{2} . 7.7 + 6 . C_{7}^{2} . 7 + 6.7 . C_{7}^{2} = 2499$ cách.

2) Xét bài toán chọn 4 đại biểu đủ cả 3 nước mà toàn nam, dẫn đến các trường hợp:2A – 1B – 1C, 1A – 2B – 1C, 1A – 1B – 2C được $C_{4}^{2} . 5.5 + 4 . C_{5}^{2} . 5 + 4.5 . C_{5}^{2} = 550$ cách.

3) Xét bài toán chọn 4 người đủ cả 3 nước toàn nữ: tương tự ta được 12 cách.

4) Vậy số trường hợp chọ được 4 đại biểu để mỗi nước đều có ít nhất một đại viểu và có cat đại biểu nam và đại biểu nữ là: 2499 – 550 – 12 = 1937

Vậy P= $\frac{1937}{4845}$

Câu 49:

Trong không gian Oxyz, cho mặt cầu (S): $(x + 1)^{2} + (y + 2)^{2} + z^{2} = 4$ và các điểm A(-2;0;-2 $\sqrt{2}$ ), B(-4;-4;0). Biết rằng tập hợp các điểm M thuộc (S) và thỏa mãn ${MA}^{2} + \vec{MO} . \vec{MB} = 16$ là đường tròn. Tính bán kính đường tròn đó.

A. $\frac{3 \sqrt{2}}{4}$

B. $\frac{3}{2}$

C. $\frac{3 \sqrt{7}}{4}$

D. $\frac{5}{2}$

Xem đáp án

Câu 50: