Câu hỏi:
06/11/2024 5,144Trong không gian Oxyz cho mặt cầu (S):. Gọi là mặt phẳng đi qua hai điểm A(0;0;-4), B(2;0;0) và cắt (S) theo giao tuyến là đường tròn (C) sao cho khối nón có đỉnh là tâm của (S), đáy là (C) có thể tích lớn nhất. Biết mặt phẳng có phương trình dạng ax + by - z + c = 0, khi đó a - b + c bằng:
A. -4.
B. 8
C. 0
D. 2
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: A
*Lời giải:
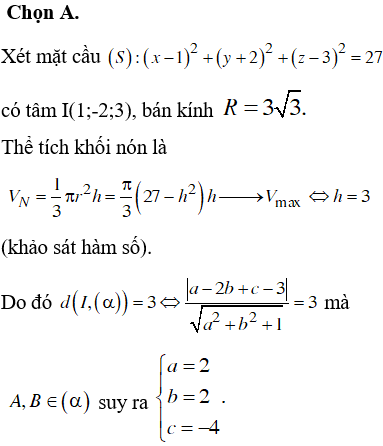
*Phương pháp giải:
- áp dụng phương trình mặt cầu tìm ra tâm I (-a,-b,-c) và bán kính R
- từ thể tích khối nón đạt giá trị max --> tính ra chiều cao h
*Cách giải và các dạng bài toán về phương trình mặt cầu và thể tích khối nón:
Trong không gian Oxyz, mặt cầu (S) tâm I (a; b; c) và bán kính R có phương trình là
(1).
Phương trình mặt cầu nói trên có thể viết dưới dạng
(2) với
Từ đó ta có phương trình (2) với điều kiện là phương trình mặt cầu tâm I (-a; -b; -c) có bán kính là
Đặc biệt nếu mặt cầu (S) có thì phương trình mặt cầu (S) là
Các dạng bài tập và cách viết phương trình mặt cầu
Dạng 1: Xác định tâm và bán kính mặt cầu – Điều kiện để (S) là một mặt cầu
Phương pháp giải:
Xét phương trình :
Khi đó mặt cầu có tâm I (a; b; c), bán kính R
+) Xét phương trình :
Khi đó mặt cầu có:
Điều kiện để (S) là phương trình mặt cầu là
+) Đặc biệt: , suy ra (S) có
Dạng 2: Viết phương trình mặt cầu khi biết tâm và bán kính
Phương pháp giải:
Bước 1: Xác định tâm I (a; b; c).
Bước 2: Xác định bán kính R của (S).
Bước 3: Thế vào phương trình (S):
Dạng phương trình mặt cầu (S) có tâm I (a; b; c) và bán kính R.
Dạng 3: Viết phương trình mặt cầu biết tâm và tiếp xúc với mặt phẳng
Phương pháp giải:
Cho điểm I (a; b; c) và mặt phẳng (P): Ax + By + Cz + D = 0
Vì mặt cầu tiếp xúc với mặt phẳng nên ta có
Từ đó viết được phương trình mặt cầu tâm I và bán kính R đã tính phía trên.
Dạng 4: Viết phương trình mặt cầu biết tâm và tiếp xúc với đường thẳng
Phương pháp giải:
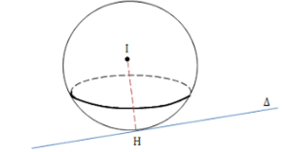
Cho điểm I (a; b; c) và đường thẳng d.
Gọi H là tiếp điểm của đường thẳng d và mặt cầu tâm I. Tìm H.
Khi đó bán kính của mặt cầu R = IH.
Công thức tính thể tích khối nón
Cho khối nón tròn xoay có diện tích đáy là S; chiều cao là h.
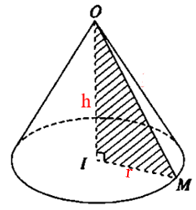
Khi đó :
Xem thêm các bài viết liên quan hay, chi tiết
Phương trình mặt cầu (lý thuyết và cách giải các dạng bài tập)
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số y = f(x). Hàm số y = f'(x) có đồ thị như hình bên.
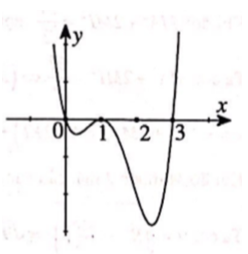
Tìm m để hàm số có 3 điểm cực trị?
Câu 3:
Cho hàm số y = f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y = f'(x) như hình vẽ bên. Xét hàm số g(x) = f(x2 - 3) và các mệnh đề sau:
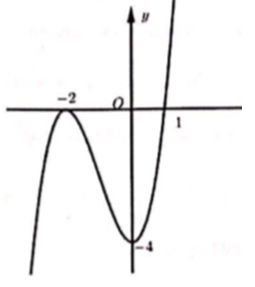
1. Hàm số g(x) có 3 điểm cực trị.
2. Hàm số g(x)đạt cực tiểu tại x = 0.
3. Hàm số g(x)đạt cực đại tại x = 2.
4. Hàm số g(x)đồng biến trên khoảng (-2;0).
5. Hàm số g(x)nghịch biến trên khoảng (-1;1).
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
Câu 4:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = 3, BC = 4, đường thẳng SA vuông góc với mặt phẳng (ABC), SA = 4. Gọi AM, AN lần lượt là chiều cao của tam giác SAB và SAC. Thể tích khối tứ diện AMNC là
Câu 5:
Cho ba số a, b, c, d theo thứ tự tạo thành cấp số nhân với công bội khác 1. Biết tổng ba số hạng đầu bằng , đồng thời theo thứ tự đó chúng lần lượt là số hạng thứ nhất, thứ tư và thứ tám của một cấp số cộng. Tính giá trị biểu thức T = a - b + c - d?
Câu 6:
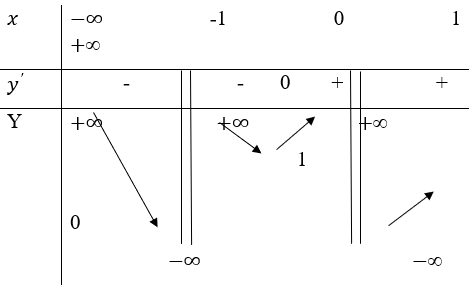
Hàm số y = f(x) xác định và có đạo hàm trên R\{-1;1} có bảng biến thiên như hình bên. Đồ thị hàm số y = f(x) có tất cả bao nhiêu đường tiệm cận (đứng và ngang)?
Câu 8:
Cho hàm số f(x) = với m là tham số thực, m > 1. Gọi S là tập tất cả các giá trị nguyên dương của m để hàm số có giá trị lớn nhất trên đoạn [0;4] nhỏ hơn 3. Số phần tử của tập S là
Câu 9:
Biết rằng phương trình (b,c∈R) có một nghiệm phức là z = 1 + 2i. Khẳng định nào sau đây là đúng?
Câu 10:
Xét bất phương trình . Nếu đặt thì phương trình trở thành bất phương trình nào sau đây?
Câu 11:
Tính thể tích V của khối lập phương ABCD.A' B' C' D' , biết AC'=a
Câu 13:
Cho x, y là các số thực dương thay đổi. Xét hình chóp S.ABC có SA = x, BC = y, các cạnh còn lại đều bằng 1. Khi thể tích khối chóp S.ABC đạt giá trị lớn nhất thì tích x + y bằng:
Câu 14:
Trong không gian với hệ tọa độ Oxyz, cho điểm M thuộc mặt cầu (S): và ba điểm A(1;0;0); B(2;1;3); C(0;2;-3). Biết rằng quỹ tích các điểm M thỏa mãn là đường tròn cố định, tính bán kính r đường tròn này.
Câu 15:
Trong không gian Oxyz, mặt cầu tâm I(1;2;3) cắt mặt phẳng : 2x - y - 2z + 18 = 0 theo một đường tròn có chu vi bằng có phương trình là:



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)