Giải SBT Toán 10 trang 60 Tập 2 Kết nối tri thức

Giải SBT Toán 10 trang 60 Tập 2 Kết nối tri thức

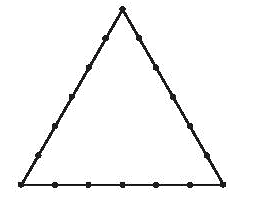
Bài 8.33 trang 60 SBT Toán 10 Tập 2: Trong hình sau đây, mỗi cạnh của tam giác đều được chia thành 6 đoạn thẳng bằng nhau bởi 5 điểm nằm bên trong cùng với hai đầu mút. Hỏi có bao nhiêu tam giác có đỉnh là các chấm điểm ở trong hình:

Lời giải:

Tổng số chấm điểm trong hình là 18.

Mỗi tam giác cần đếm được tạo ra bằng cách lấy ra 3 điểm không thẳng hàng. Để đếm số các tam giác ta lấy số các cách lấy ra 3 điểm từ 18 điểm trừ đi số các cách lấy ra 3 điểm thẳng hàng từ 18 điểm.

Số các cách chọn 3 điểm từ 18 điểm là:

$C_{18}^3=\frac{18!}{3!(18-3)!}=816$ (cách).

Ba điểm thẳng hàng nếu chúng nằm trên cùng một cạnh. Số điểm của mỗi cạnh là 7. Do đó, số cách lấy ra 3 điểm trên mỗi cạnh là:

$C_7^3=\frac{7!}{3!(7-3)!}=35$ (cách).

Như vậy, theo quy tắc cộng thì số các cách chọn ra 3 điểm thẳng hàng từ hình trên là:

35 + 35 + 35 = 105 (cách).

Suy ra số các tam giác cần tìm là:

816 – 105 = 711 (tam giác).

Bài 8.34 trang 60 SBT Toán 10 Tập 2: Hình sau đây được tạo thành từ hai họ đường thẳng vuông góc, mỗi họ gồm 6 đường thẳng song song.

Hỏi có bao nhiêu hình chữ nhật khác nhau được tạo thành ?

Lời giải:

Trong hình đã cho, mỗi hình chữ nhật được tạo thành từ giao điểm của 2 đường thẳng của họ các đường thẳng nằm ngang và 2 đường thẳng của họ các đường thẳng nằm dọc.

Số cách chọn ra 2 đường thẳng từ 6 đường thẳng nằm ngang là:

$C_6^2=\frac{6!}{2!(6-2)!}=15$ (cách).

Tương tự, số cách chọn ra 2 đường thẳng nằm dọc cũng là: $C_6^2=\frac{6!}{2!(6-2)!}=15$  cách.

Vì vậy, theo quy tắc nhân thì số hình chữ nhật được tạo ra là:

15 . 15 = 225 (hình).

Bài 8.35 trang 60 SBT Toán 10 Tập 2:

a) Có bao nhiêu dãy kí tự gồm 4 chữ cái (có thể là vô nghĩa) được tạo thành bằng cách sắp xếp các chữ cái của từ “NGHI”?

b) Có bao nhiêu dãy kí tự gồm 6 chữ cái (có thể là vô nghĩa) được tạo thành bằng cách sắp xếp các chữ cái của từ “NGHIÊN”?

c) Có bao nhiêu dãy kí tự gồm 7 chữ cái (có thể là vô nghĩa) được tạo thành bằng cách sắp xếp các chữ cái của từ “NGHIÊNG”?

Lời giải:

a)

Từ “NGHI” có 4 chữ cái khác nhau là "N, G, H, I". Số cách sắp xếp chúng theo yêu cầu bằng số các hoán vị của 4 chữ cái, bằng: 4 . 3 . 2 . 1 = 24 (dãy).

b)

Từ “NGHIÊN” có 6 chữ cái, trong đó có 2 chữ cái giống nhau là “N, N”.

Việc xếp các chữ cái “N, G, H, I, Ê, N” của từ “NGHIÊN” theo yêu cầu giống như việc bỏ các chữ cái “N,G, H, I, Ê, N” vào 6 hộp, mỗi hộp có 1 chữ cái:

Việc bỏ các chữ cái “N, G, H, I, Ê, N” vào 6 chiếc hộp có thể thực hiện qua 2 công đoạn.

– Công đoạn 1: chọn 2 chiếc hộp trong 6 chiếc hộp rồi bỏ 2 chữ cái N, N vào 2 chiếc hộp đó;

– Công đoạn 2: bỏ các chữ cái G, H, I, Ê vào 4 chiếc hộp còn lại;

Số cách thực hiện công đoạn 1 bằng số các cách chọn 2 hộp từ 6 hộp, do đó bằng:

$C_6^2=\frac{6!}{2!(6-2)!}=15$ (cách)

Số cách thực hiện công đoạn 2 bằng số các hoán vị của 4 chữ cái, do đó bằng:

4! = 4 . 3 . 2 . 1 = 24 (cách) .

Như vậy, theo quy tắc nhân thì số dãy kí tự được tạo thành là: 15 . 24 = 360 (dãy).

c)

Từ “NGHIÊNG” có 7 chữ cái: “N, G, H, I, Ê, N, G”, trong đó có các chữ cái giống nhau là “N, N” và “G, G”.

Việc xếp các chữ cái “N,G, H, I, Ê, N, G” của từ “NGHIÊNG” thành một dãy kí tự có 7 chữ cái giống như việc bỏ các chữ cái “N,G, H, I, Ê, N, G” vào 7 hộp (có thứ tự).

Việc bỏ các chữ cái “N, G, H, I, Ê, N, G” vào 7 cái hộp có thể thực hiện qua 2 công đoạn.

– Công đoạn 1: chọn 2 cái hộp trong 7 cái hộp rồi bỏ các chữ cái N, N vào 2 chiếc hộp đó;

– Công đoạn 2: chọn 2 cái hộp trong 5 cái hộp còn lại rồi bỏ các chữ cái G, G vào 2 chiếc hộp đó;

– Công đoạn 3: bỏ các chữ cái H, I, Ê vào 3 chiếc hộp còn lại.

Số cách thực hiện công đoạn 1 bằng số cách chọn 2 hộp từ 7 hộp, nghĩa là bằng:

$C_7^2=\frac{7!}{2!(7-2)!}=21$ (cách).

Số cách thực hiện công đoạn 2 bằng số cách chọn 2 hộp từ 5 hộp, nghĩa là bằng:

$C_5^2=\frac{5!}{2!(5-2)!}=10$(cách).

Số cách thực hiện công đoạn 3 bằng số các hoán vị của 3, nghĩa là bằng:

3! = 3 . 2 . 1 = 6 (cách).

Như vậy, theo quy tắc nhân thì số dãy kí tự được tạo thành là:

21 . 10 . 6 = 1 260 (dãy).

Bài 8.36 trang 60 SBT Toán 10 Tập 2: Tính ${\left(\sqrt{3}+\sqrt{2}\right)}^5-{\left(\sqrt{3}-\sqrt{2}\right)}^5$ .

Lời giải:

Áp dụng công thức khai triển của (a + b)⁵ lần lượt với $a=\sqrt{3}$  và $b=\sqrt{2}$ , rồi $a=\sqrt{3}$  và $b=-\sqrt{2}$, ta có

$$\begin{gathered} {\left(\sqrt{3}+\sqrt{2}\right)}^5-{\left(\sqrt{3}-\sqrt{2}\right)}^5 \\ =\left({\left(\sqrt{3}\right)}^5+5{\left(\sqrt{3}\right)}^4.\sqrt{2}+10{\left(\sqrt{3}\right)}^3.{\left(\sqrt{2}\right)}^2+10{\left(\sqrt{3}\right)}^2.{\left(\sqrt{2}\right)}^3+5\sqrt{3}.{\left(\sqrt{2}\right)}^4+{\left(\sqrt{2}\right)}^5\right) \\ -\left({\left(\sqrt{3}\right)}^5-5{\left(\sqrt{3}\right)}^4.\sqrt{2}+10{\left(\sqrt{3}\right)}^3.{\left(\sqrt{2}\right)}^2-10{\left(\sqrt{3}\right)}^2.{\left(\sqrt{2}\right)}^3+5\sqrt{3}.{\left(\sqrt{2}\right)}^4-{\left(\sqrt{2}\right)}^5\right) \\ =10{\left(\sqrt{3}\right)}^4.\sqrt{2}+20{\left(\sqrt{3}\right)}^2.{\left(\sqrt{2}\right)}^3+2{\left(\sqrt{2}\right)}^5 \\ =\mathrm{10.9.}\sqrt{2}+\mathrm{20.3.2}\sqrt{2}+2.4\sqrt{2} \\ =218\sqrt{2} \end{gathered}$$

Bài 8.37 trang 60 SBT Toán 10 Tập 2: Giả sử hệ số của x trong khai triển của ${\left(x^2+\frac{r}{x}\right)}^5$ bằng 640. Xác định giá trị của r.

Lời giải:

Áp dụng công thức khai triển của (a + b)⁵ cho $a=x^2,b=\frac{r}{x}$  ta được:

$$\begin{gathered} {\left(x^2+\frac{r}{x}\right)}^5 \\ =C_5^0.{\left(x^2\right)}^5+C_5^1.{\left(x^2\right)}^4.\frac{r}{x}+C_5^2.{\left(x^2\right)}^3.{\left(\frac{r}{x}\right)}^2+C_5^3.{\left(x^2\right)}^2.{\left(\frac{r}{x}\right)}^3+C_5^4.x^2.{\left(\frac{r}{x}\right)}^4+C_5^5.{\left(\frac{r}{x}\right)}^5 \\ ={\left(x^2\right)}^5+5{\left(x^2\right)}^4.\frac{r}{x}+10{\left(x^2\right)}^3.{\left(\frac{r}{x}\right)}^2+10{\left(x^2\right)}^2.{\left(\frac{r}{x}\right)}^3+5x^2.{\left(\frac{r}{x}\right)}^4+{\left(\frac{r}{x}\right)}^5 \\ =x^{10}+5r{x}^7+10r^2{x}^4+10r^{3}x+\frac{5r^4}{x^2}+\frac{r^5}{x^5} \end{gathered}$$

Theo đề bài, ta có hệ số của x trong khai triển của ${\left(x^2+\frac{r}{x}\right)}^5$ bằng 640 nên:

10r³ = 640

⇔ r³ = 64

⇔ r = 4

Vậy r = 4 .

Xem thêm lời giải sách bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác: 

Giải SBT Toán 10 trang 58 Tập 2

Giải SBT Toán 10 trang 59 Tập 2