Giải SBT Toán 10 trang 54 Tập 1 Kết nối tri thức
Với Giải SBT Toán 10 trang 54 Tập 1 trong Bài 9: Tích của một vectơ với một số Toán lớp 10 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 10 trang 54.
Giải SBT Toán 10 trang 54 Tập 1 Kết nối tri thức
Bài 4.13 trang 54 SBT Toán 10 Tập 1:
Cho tam giác ABC. Gọi D, E tương ứng là trung điểm của BC, CA. Hãy biểu thị các vectơ theo hai vectơ và
Lời giải:
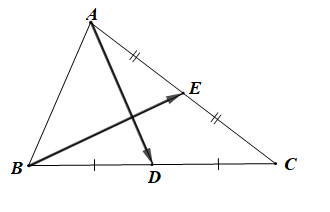
Ta có:
+) D là trung điểm của BC nên
+) E là trung điểm của AC nên
Do đó
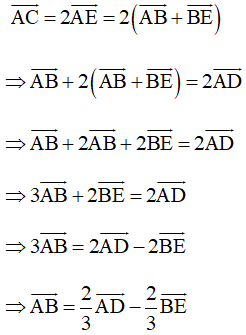
+) Vì nên
Mà
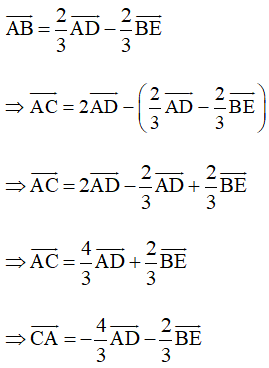
+) (quy tắc hiệu)
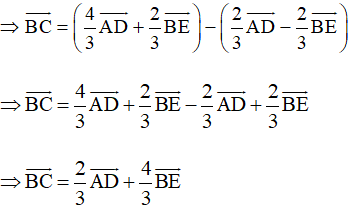
Vậy và
Bài 4.14 trang 54 SBT Toán 10 Tập 1:
Cho tam giác OAB vuông cân, với OA = OB = a. Hãy xác định độ dài của các vectơ sau
Lời giải:
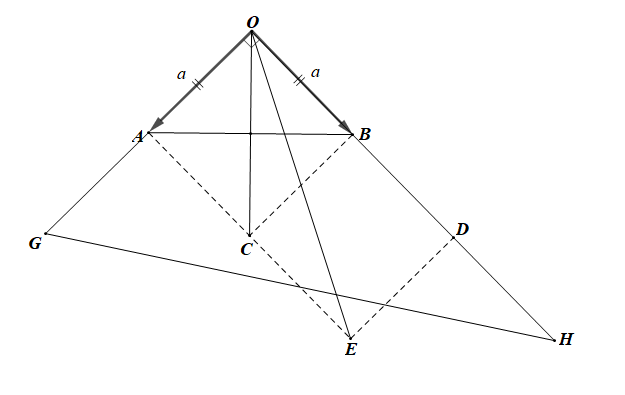
Gọi C là điểm thoả mãn OACB là hình bình hành
Mà ∆OAB vuông cân có OA = OB nên OACB là hình vuông
OC = AB
Mà AB2 = OA2 + OB2 (định lí Pythagoras)
AB2 = a2 + a2 = 2a2
+) Có: (quy tắc hình bình hành)
+) Có:
+) Lấy điểm D sao cho nên hai vectơ , cùng hướng và OD = 2OB.
Có:
Vẽ hình chữ nhật OAED, khi đó
Mà OE2 = OD2 + DE2 (định lí Pythagoras)
OE2 = (2OB)2 + OA2
OE2 = (2a)2 + a2 = 5a2
Do đó
+) Lấy điểm G sao cho
Khi đó: hai vectơ , cùng hướng và OG = 2OA;
Và hai vectơ , cùng hướng và OH = 3OB.
Có:
Mà HG2 = OG2 + OH2 (định lí Pythagoras)
HG2 = (2OA)2 + (3OB)2
HG2 = (2a)2 + (3a)2
HG2 = 13a2
Do đó
Vậy và
Bài 4.15 trang 54 SBT Toán 10 Tập 1:
Cho tam giác ABC có trực tâm H, trọng tâm G và tâm đường tròn ngoại tiếp O.
a) Gọi M là trung điểm của BC. Chứng minh rằng
b) Chứng minh rằng
c) Chứng minh rằng ba điểm G, H, O cùng thuộc một đường thẳng.
Lời giải:
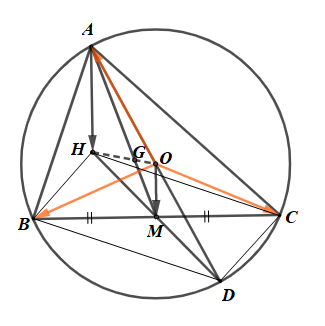
a) Kẻ đường kính AD.
Hai điểm B, C thuộc đường tròn đường kính AD nên
Hay BD ⊥ AB, CD ⊥ AC
Lại có H là trực tâm ∆ABC nên BH ⊥ AC, CH ⊥ AB
BH /// CD và CH // BD
BHCD là hình bình hành (dấu hiệu nhận biết)
Hai đường chéo cắt nhau tại trung điểm của mỗi đường (tính chất hình bình hành)
Mà M là trung điểm của BC
M là trung điểm của HD
Mà O là trung điểm của AD
Khi đó OM là đường trung bình của ∆AHD
OM // AH và (tính chất đường trung bình)
Do đó hai vectơ và có:
+ Cùng phương, cùng hướng
+ Độ dài:
Vậy
b) Vì M là trung điểm của BC nên
Mà (câu a)
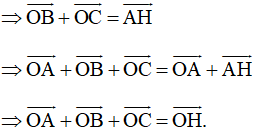
Vậy
c) Vì G là trọng tâm tam giác ABC nên
Mà (câu b)
Suy ra
Khi đó và cùng phương, cùng hướng
O, H, G thẳng hàng.
Vậy ba điểm O, H, G thẳng hàng.
Bài 4.16 trang 54 SBT Toán 10 Tập 1:
Cho tứ giác ABCD. Gọi M, N theo thứ tự là trung điểm các cạnh AB, CD và gọi I là trung điểm của MN. Chứng minh rằng với điểm O bất kì đều có
Lời giải:
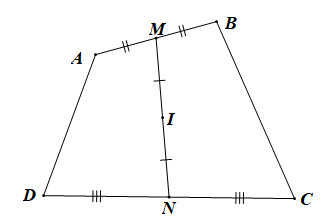
Với điểm O bất kì ta có:
+) (do M là trung điểm của AB)
+) (do N là trung điểm của CD)
+) (do I là trung điểm của MN)
Vậy với điểm O bất kì đều có:
Bài 4.17 trang 54 SBT Toán 10 Tập 1:
Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S theo thứ tự là trung điểm của các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.
Lời giải:
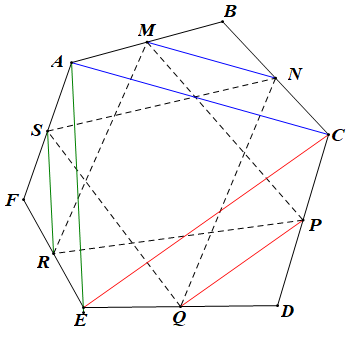
+) Vì M, N lần lượt là trung điểm của AB, BC
Nên MN là đường trung bình của tam giác ABC.
MN // AC và (tính chất đường trung bình)
Do đó (1)
Chứng minh tương tự ta cũng có: (2)
Và (3)
Từ (1), (2) và (3) ta có:
(quy tắc ba điểm)
(quy tắc ba điểm)
Do đó
+) Giả sử G và G' lần lượt là trọng tâm của tam giác MPR và tam giác NQS.
Khi đó ta có: và hay
Mặt khác: theo quy tắc ba điểm ta có:
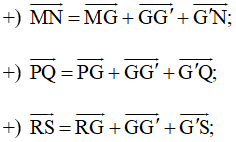
+) Lại có (chứng minh trên)
Nên
Suy ra G và G' trùng nhau.
Vậy hai tam giác MPR và NQS có cùng trọng tâm.
Bài 4.18 trang 54 SBT Toán 10 Tập 1:
Cho tam giác ABC đều với trọng tâm O. M là một điểm tuỳ ý nằm trong tam giác. Gọi D, E, F theo thứ tự là hình chiếu vuông góc của M trên BC, CA, AB.
Chứng minh rằng
Lời giải:
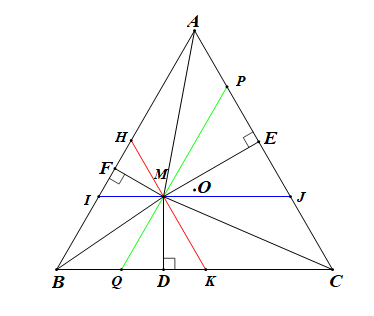
Qua M, kẻ các đường thẳng IJ // BC, HK // AC, PQ // AB.
Tam giác ABC đều nên
Mà PQ // AB nên
HK // AC nên
Tam giác MQK có: nên là tam giác đều.
Lại có MD là đường cao kẻ từ M nên MD đồng thời là đường trung tuyến
Do đó D là trung điểm của QK
(1)
Chứng minh tương tự ta cũng có:
+) (2)
+) (3)
Từ (1), (2) và (3) ta có:
Vì MI // BQ, MQ // BI nên tứ giác MIBQ là hình bình hành
Tương tự ta có
Khi đó
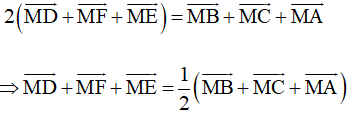
Lại có O là trọng tâm của tam giác ABC nên
Vậy
Bài 4.19 trang 54 SBT Toán 10 Tập 1:
Cho tam giác ABC.
a) Tìm điểm M sao cho
b) Xác định điểm N thoả mãn
Lời giải:
a)
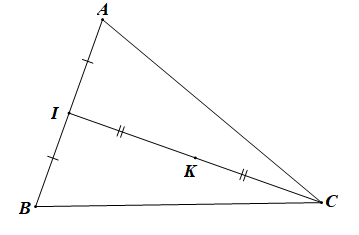
Gọi I là trung điểm của AB.
Khi đó:
Gọi K là trung điểm của IC, khi đó:
Mà
Do đó
Suy ra M ≡ K.
Vậy M là trung điểm của IC (với I là trung điểm của AB).
b)
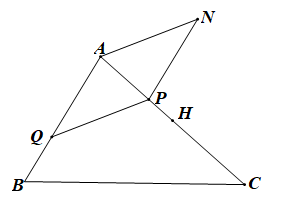
Ta có:
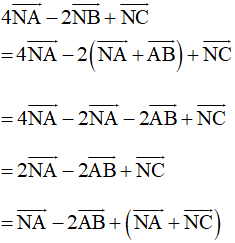
Gọi H là trung điểm của AC, khi đó
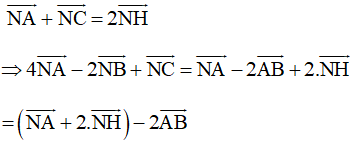
Giả sử P là điểm thỏa mãn
Khi đó
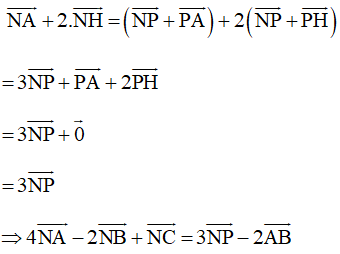
Mà
Nên
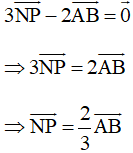
Gọi Q là điểm nằm trên cạnh AB sao cho
Do đó tứ giác AQPN là hình bình hành
Vậy điểm N cần tìm là đỉnh của hình bình hành AQPN (với Q thỏa mãn và P thỏa mãn , H là trung điểm của AC).
Xem thêm lời giải sách bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:
Giải SBT Toán 10 trang 55 Tập 1
Xem thêm lời giải sách bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:
Bài 6: Hệ thức lượng trong tam giác
Xem thêm các chương trình khác:
- Soạn văn lớp 10 (hay nhất) – Kết nối tri thức
- Tác giả tác phẩm Ngữ văn lớp 10 – Kết nối tri thức
- Soạn văn lớp 10 (ngắn nhất) – Kết nối tri thức
- Tóm tắt tác phẩm Ngữ văn lớp 10 - KNTT
- Bố cục tác phẩm Ngữ văn lớp 10 – Kết nối tri thức
- Nội dung chính tác phẩm Ngữ văn lớp 10 – Kết nối tri thức
- Văn mẫu lớp 10 – Kết nối tri thức
- Giải Chuyên đề học tập Ngữ văn 10 – Kết nối tri thức
- Giải sgk Tiếng Anh 10 Global Success – Kết nối tri thức
- Giải sbt Tiếng Anh 10 Global Success – Kết nối tri thức
- Ngữ pháp Tiếng Anh 10 Global success
- Bài tập Tiếng Anh 10 Global success theo Unit có đáp án
- Trọn bộ Từ vựng Tiếng Anh 10 Global success đầy đủ nhất
- Giải sgk Vật lí 10 – Kết nối tri thức
- Giải sbt Vật lí 10 – Kết nối tri thức
- Giải Chuyên đề Vật lí 10 – Kết nối tri thức
- Lý thuyết Vật lí 10 – Kết nối tri thức
- Chuyên đề dạy thêm Vật lí 10 cả 3 sách (2024 có đáp án)
- Giải sgk Hóa học 10 – Kết nối tri thức
- Lý thuyết Hóa học 10 – Kết nối tri thức
- Giải sbt Hóa học 10 – Kết nối tri thức
- Giải Chuyên đề Hóa học 10 – Kết nối tri thức
- Chuyên đề dạy thêm Hóa 10 cả 3 sách (2024 có đáp án)
- Giải sgk Sinh học 10 – Kết nối tri thức
- Giải sbt Sinh học 10 – Kết nối tri thức
- Lý thuyết Sinh học 10 – Kết nối tri thức
- Giải Chuyên đề Sinh học 10 – Kết nối tri thức
- Giải sgk Lịch sử 10 – Kết nối tri thức
- Giải sbt Lịch sử 10 – Kết nối tri thức
- Giải Chuyên đề Lịch sử 10 – Kết nối tri thức
- Lý thuyết Lịch sử 10 - Kết nối tri thức
- Giải sgk Địa lí 10 – Kết nối tri thức
- Lý thuyết Địa Lí 10 – Kết nối tri thức
- Giải sbt Địa lí 10 – Kết nối tri thức
- Giải Chuyên đề Địa lí 10 – Kết nối tri thức
- Giải sgk Công nghệ 10 – Kết nối tri thức
- Lý thuyết Công nghệ 10 – Kết nối tri thức
- Giải sgk Giáo dục Kinh tế và Pháp luật 10 – Kết nối tri thức
- Giải sbt Giáo dục Kinh tế và Pháp luật 10 – Kết nối tri thức
- Giải Chuyên đề Kinh tế và pháp luật 10 – Kết nối tri thức
- Lý thuyết KTPL 10 – Kết nối tri thức
- Giải sgk Giáo dục quốc phòng - an ninh 10 – Kết nối tri thức
- Lý thuyết Giáo dục quốc phòng 10 – Kết nối tri thức
- Giải sbt Giáo dục quốc phòng 10 – Kết nối tri thức
- Giải sgk Hoạt động trải nghiệm 10 – Kết nối tri thức
- Giải sbt Hoạt động trải nghiệm 10 – Kết nối tri thức
- Giải sgk Tin học 10 – Kết nối tri thức
- Lý thuyết Tin học 10 – Kết nối tri thức
- Giải sbt Tin học 10 – Kết nối tri thức
- Giải Chuyên đề Tin học 10 – Kết nối tri thức
- Giải sgk Giáo dục thể chất 10 – Kết nối tri thức
