Lý thuyết Tổng hợp kiến thức cơ bản (mới 2022 + Bài Tập) - Toán lớp 4

Lý thuyết Tổng hợp kiến thức cơ bản lớp 4

SỐ TỰ NHIÊN

1. Số và chữ số

- Dùng 10 chữ số để viết số là: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

·      Có 10 số có 1 chữ số (từ 0 đến 9)

·      Có 90 số có 2 chữ số (từ 10 đến 99)

·      Có 900 số có 3 chữ số (từ 100 đến 999)

·      Có 9000 số có 4 chữ số (từ 1000 đến 9999)

- Số tự nhiên nhỏ nhất là số 0. Không có số tự nhiên lớn nhất.

- Hai số tự nhiên liên tiếp hơn (kém) nhau một đơn vị.

- Các số có chữ số tận cùng là 0, 2, 4, 6, 8 gọi là số chẵn. Hai số chẵn liên tiếp hơn kém nhau 2 đơn vị.

- Các số có chữ số tận cùng là 1, 3, 5, 7, 9 gọi là số lẻ. Hai số lẻ liên tiếp hơn kém nhau 2 đơn vị.

2. Hàng và lớp

* Lớp nghìn

Hàng đơn vị, hàng chục, hàng trăm hợp thành lớp đơn vị.

Hàng nghìn, hàng chục nghìn, hàng nghìn hợp thành lớp nghìn.

3. Triệu và lớp triệu

 BIỂU THỨC

A. Các loại biểu thức thường gặp

1. Biểu thức có chứa một chữ

Ví dụ: 3 + a là biểu thức có chứa một chữ

+ Nếu a = 1 thì 3 + a = 3 + 1 = 4; 4 là giá trị của biểu thức 3 + a

+ Nếu a = 2 thì 3 + a = 3 + 2 = 5; 5 là giá trị của biểu thức 3 + a

+ Nếu a = 3 thì 3 + a = 3 + 3 = 6; 6 là giá trị của biểu thức 3 + a

2. Biểu thức có chứa hai chữ

Ví dụ: a + b là biểu thức có chứa hai chữ

+ Nếu a = 3 và b = 2 thì a + b = 3 + 2 = 5; 5 là giá trị của biểu thức a + b

+ Nếu a = 4 và b = 0 thì a + b = 4 + 0 = 4; 4 là giá trị của biểu thức a + b

+ Nếu a = 0 và b = 1 thì a + b = 0 + 1 = 1; 1 là giá trị của biểu thức a + b

Mỗi lần thay chữ số bằng số ta tính được một giá trị của biểu thức a + b.

3. Biểu thức có chứa ba chữ

Ví dụ: a + b + c  là biểu thức có chứa ba chữ

+ Nếu a = 2, b = 3 và c = 4 thì a + b + c = 2 + 3 + 4 = 5 + 4 = 9

+ Nếu a = 5, b = 1 và c = 0 thì a + b + c = 5 + 1 + 0 = 6 + 0 = 6

+ Nếu a = 1, b = 0 và c = 2 thì a + b + c = 1 + 0 + 2 = 1 + 2 = 3

B. Cách tính giá trị của biểu thức

1. Biểu thức không có dấu ngoặc đơn chỉ có phép cộng và phép trừ (hoặc chỉ có phép nhân và phép chia) thì ta thực hiện các phép tính theo thứ tự từ trái sang phải.

Ví dụ:

a) 542 + 123 – 79 = 665 – 79 = 586              b) 482 x 2 : 4 = 964 : 4 = 241

2. Biểu thức không có dấu ngoặc đơn, có các phép tính cộng, trừ, nhân, chia thì ta thực hiện các phép tính nhân, chia trước rồi thực hiện các phép tính cộng trừ sau.

Ví dụ: 27 : 3 - 4 x 2 = 9 - 8 = 1

3. Biểu thức có dấu ngoặc đơn thì ta thực hiện các phép tính trong ngoặc đơn trước, các phép tính ngoài dấu ngoặc đơn sau.

Ví dụ: 25 x (21 + 120) = 25 x 141 = 3525

 BỐN PHÉP TÍNH VỚI SỐ TỰ NHIÊN

A. PHÉP CỘNG

1. Tính chất giao hoán

a + b = b + a

Ví dụ: 2 + 3 = 3 + 2

2. Tính chất kết hợp của phép cộng

(a + b) + c = a + (b + c)

Ví dụ: (2 + 3) + 4 = 2 + (3 + 4)

3. Cộng với 0

0 + a = a + 0 = a

Ví dụ: 0 + 9 = 9 + 0

Nhận xét:

+ Trong một tổng có số lượng các số hạng lẻ là lẻ thì tổng đó là một số lẻ.

+ Trong một tổng có số lượng các số hạng lẻ là chẵn thì tổng đó là một số chẵn.

+ Tổng của các số chẵn là một số chẵn.

+ Tổng của một số lẻ và một số chẵn là một số lẻ.

+ Tổng của hai số tự nhiên liên tiếp là một số lẻ.

B. PHÉP TRỪ

1. a - (b + c) = (a - c) - b = (a - b) - c

2. Nếu số bị trừ và số trừ cùng tăng (hoặc giảm) n đơn vị thì hiệu của chúng không đổi.

3. Nếu số bị trừ được gấp lên n lần và giữ nguyên số trừ thì hiệu được tăng thêm một số đúng bằng (n - 1) lần số bị trừ (n > 1).

4. Nếu số bị trừ giữ nguyên, số trừ được gấp lên n lần thì hiệu bị giảm đi (n - 1) lần số trừ (n > 1).

5. Nếu số bị trừ được tăng thêm n đơn vị, số trừ giữ nguyên thì hiệu tăng lên n đơn vị.

6. Nếu số bị trừ tăng lên n đơn vị, số trừ giữ nguyên thì hiệu giảm đi n đơn vị.

C. PHÉP NHÂN

1. Tính chất giao hoán

a x b = b x a

Ví dụ: 2 x 3 = 3 x 2

2. Tính chất kết hợp

a x (b x c) = (a x b) x c

Ví dụ: 2 x (3 x 4) = (2 x 3) x 4

3. Nhân với 0

a x 0 = 0 x a = 0

Ví dụ: 2 x 0 = 0 x 2 = 0

4. Nhân với 1

a x 1 = 1 x a = a

Ví dụ: 4 x 1 = 1 x 4 = 4

5. Tính chất phân phối của phép nhân với phép cộng

a x (b + c) = a x b + a x c

Ví dụ: 3 x (2 + 3) = 3 x 2 + 3 x 3

6. Tính chất phân phối của phép nhân với phép trừ

a x (b - c) = a x b - a x c

Ví dụ: 6 x (9 – 3) = 6 x 9 – 6 x 3

7. Trong một tích nếu một thừa số được gấp lên n lần đồng thời có một thừa số khác bị giảm đi n lần thì tích không thay đổi.

8. Trong một tích có một thừa số được gấp lên n lần, các thừa số còn lại giữ nguyên thì tích được gấp lên n lần và ngược lại nếu trong một tích có một thừa số bị giảm đi n lần, các thừa số còn lại giữ nguyên thì tích cũng bị giảm đi n lần. (n > 0)

9.  Trong một tích, nếu một thừa số được gấp lên n lần, đồng thời một thừa số được gấp lên m lần thì tích được gấp lên (m x n) lần. Ngược lại nếu trong một tích một thừa số bị giảm đi m lần, một thừa số bị giảm đi n lần thì tích bị giảm đi (m x n) lần (m và n khác 0).

10. Trong một tích, nếu một thừa số được tăng thêm a đơn vị, các thừa số còn lại giữ nguyên thì tích được tăng thêm a lần tích các thừa số còn lại.

11. Trong một tích, nếu có ít nhất một thừa số chẵn thì tích đó chẵn.

12. Trong một tích, nếu có ít nhất một thừa số tròn chục hoặc ít nhất một thừa số có tận cùng là 5 và có ít nhất một thừa số chẵn thì tích có tận cùng là 0.

13. Trong một tích các thừa số đều lẻ và có ít nhất một thừa số có tận cùng là 5 thì tích có tận cùng là 5.

D. PHÉP CHIA

1.  a : (b x c) = a : b : c = a : c : b (b, c > 0)

2.  0 : a = 0 (a > 0)

3.  a : c - b : c = ( a - b) : c (c > 0)

4.  a : c + b : c = (a + b) : c (c > 0)

5.  Trong phép chia, nếu số bị chia tăng lên (giảm đi) n lần (n > 0) đồng thời số chia giữ nguyên thì thương cũng tăng lên (giảm đi) n lần.

6.  Trong một phép chia, nếu tăng số chia lên n lần (n > 0) đồng thời số bị chia giữ nguyên thì thương giảm đi n lần và ngược lại.

7. Trong một phép chia, nếu cả số bị chia và số chia đều cùng gấp (giảm) n lần (n > 0) thì thương không thay đổi.

8. Trong một phép chia có dư, nếu số bị chia và số chia cùng được gấp (giảm) n lần (n > 0) thì số dư cũng được gấp (giảm) n lần.

DÃY SỐ

1. Đối với số tự nhiên liên tiếp

a)   Dãy số tự nhiên liên tiếp bắt đầu là số chẵn kết thúc là số lẻ hoặc bắt đầu là số lẻ và kết thúc bằng số chẵn thì số lượng số chẵn bằng số lượng số lẻ.

b)    Dãy số tự nhiên liên tiếp bắt đầu bằng số chẵn và kết thúc bằng số chẵn thì số lượng số chẵn nhiều hơn số lượng số lẻ là 1.

c)     Dãy số tự nhiên liên tiếp bắt đầu bằng số lẻ và kết thúc bằng số lẻ thì số lượng số lẻ nhiều hơn số lượng số chẵn là 1.

2. Một số quy luật của dãy số thường gặp

a) Mỗi số hạng (kể từ số hạng thứ 2) bằng số hạng đứng liền trước nó cộng hoặc trừ một số tự nhiên.

Ví dụ: 2, 5, 8, 11, …

Dãy số trên được viết theo quy luật: Số hạng đứng liền sau bằng số hạng đứng liền trước cộng với 3.

b) Mỗi số hạng (kể từ số hạng thứ 2) bằng số hạng đứng liền trước nó nhân hoặc chia một số tự nhiên.

Ví dụ: 1024, 512, 256, 128, …

Dãy số trên được viết theo quy luật: Số hạng đứng liền sau bằng số hạng đứng liền trước chia cho 2.

c) Mỗi số hạng (kể từ số hạng thứ 3) bằng tổng hai số hạng đứng liền trước nó.

Ví dụ: 1, 2, 3, 5, 8, 13, 21,…

Dãy số được viết theo quy luật: Từ số hạng thứ ba, số hạng đứng sau bằng tổng hai số hạng đứng liền trước nó (3 = 2 + 1, 5 = 3 + 2, 8 = 5 + 3, ….)

3. Dãy số cách đều

*) Tìm số số hạng của dãy số cách đều

Số số hạng = (Số cuối – Số đầu) : Khoảng cách giữa hai số hạng liên tiếp + 1

Ví dụ. Tìm số số hạng của dãy số: 1, 4, 7, 10, 13, 16, 19, …, 94, 97, 100

Bài giải

Số số hạng của dãy số đã cho là:

(100 – 1) : 3 + 1 = 34 (số hạng)

Đáp số: 34 số hạng

*) Tính tổng của dãy số cách đều

Tổng = (Số đầu + Số cuối) x Số số hạng : 2

Ví dụ. Tính tổng của dãy số: 1, 4, 7, 10, 13, 16, 19, …, 94, 97, 100

Bài giải

Số số hạng của dãy số trên là: 34 số hạng

Tổng của dãy số trên là:

(100 + 1) x 34 : 2 = 1717

Đáp số: 1717

DẤU HIỆU CHIA HẾT

1. Dấu hiệu chia hết cho 2

Các số có chữ số tận cùng là 0, 2, 4, 6, 8 thì chia hết cho 2.

Ví dụ:

12, 14, 16, 18 là những số chia hết cho 2 vì có chữ số tận cùng là 2, 4, 6, 8

11, 13, 15, 17 là những số không chia hết cho 2 vì có chữ số tận cùng là 1, 3, 5, 7

- Số chia hết cho 2 là số chẵn.

- Số không chia hết cho 2 là số lẻ.

2. Dấu hiệu chia hết cho 5

Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5.

Ví dụ:

945, 3000 là những số chia hết cho 5 vì số đó có chữ số tận cùng lần lượt là 5, 0

10, 25 là những số chia hết cho 5 vì những số đó có tận cùng là 0, 5

3. Dấu hiệu chia hết cho 9

Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9.

Các số có tổng các chữ số không chia hết cho 9 thì không chia hết cho 9.

Ví dụ:

4. Dấu hiệu chia hết cho 3

Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3.

Các số có tổng các chữ số không chia hết cho 3 thì không chia hết cho 3.

Ví dụ:

$\overline{ab}=a\times 10+b$

CẤU TẠO SỐ

Sử dụng cấu tạo số:

$\overline{abc}=a\times 100+b\times 10+c$

$\overline{abcd}=\times 1000+b\times 100+c\times 10+d$

……………..

$\overline{ab}=a0+b$

$\overline{abc}=a00+b0+c$

Ví dụ: Cho số có 2 chữ số, nếu lấy tổng các chữ số cộng với tích các chữ số của số đã cho thì bằng chính số đó. Tìm chữ số hàng đơn vị của số đã cho.

Bài giải

Gọi số có 2 chữ số cần tìm là $\overline{ab}$ .

$\overline{ab}=a+b+a\times b$

10$\times$a+b= a+b+ a$\times$b

10$\times$a= a+ a$\times$b

$10\times a-a=a\times b$

$9\times a=a\times b$

b=9

Vậy chữ số hàng đơn vị của số đã cho bằng 9.

BẢNG ĐƠN VỊ ĐO KHỐI LƯỢNG

Nhận xét: Mỗi đơn vị đo khối lượng đều gấp 10 lần đơn vị bé hơn, liền nó.

Ví dụ. Đổi đơn vị:

a) 1dag = 10g                           

b) 1hg = 10 dag

c) 1 tấn = 1 000 000g               

d) 1kg30g = 1kg + 30g = 1000g + 30g = 1030g     

 GIÂY, THẾ KỈ

a) Giây

1 giờ = 60 phút

1 phút = 60 giây

b) Thế kỉ

- 1 thế kỉ = 100 năm

-  Từ năm 1 đến năm 100 là thế kỉ một (thế kỉ I)

-  Từ năm 101 đến năm 200 là thế kỉ hai (thế kỉ II)

-  Từ năm 201 đến năm 300 là thế kỉ ba (thế kỉ III)

…

-  Từ năm 1901 đến năm 2000 là thế kỉ hai mươi (thế kỉ XX)

-  Từ năm 2001 đến năm 2100 là thế kỉ hai mươi mốt (thế kỉ XXI)

Ví dụ:

1) 1 phút = 60 giây;                   2) 7 phút = 420 giây

3) 4 phút 20 giây = 4 phút + 20 giây = 240 giây + 20 giây = 260 giây

4)  ngày = 8 giờ

BÀI TOÁN TÌM SỐ TRUNG BÌNH CỘNG

1. Cách tìm số trung bình cộng

Muốn tìm số trung bình cộng của nhiều số, ta tính tổng của các số đó, rồi lấy tổng đó chia cho số các số hạng.

Ví dụ. Tìm số trung bình cộng của các số sau:

a) 42 và 54

b) 46, 72 và 59

Bài giải

a) Trung bình cộng của hai số 42 và 54 là:

$\frac{42+54}{2}=48$

b) Trung bình cộng của ba số 46, 72 và 59 là:

$\frac{46+72+59}{3}=59$

Đáp số:

a) 48        

b) 59

*) Số trung bình cộng của dãy cách đều: (số đầu + số cuối) : 2

2. Ví dụ

Tính trung bình cộng của dãy số: 5, 10, 15, 20, …, 95, 105

Bài giải

Trung bình cộng của dãy số trên là:

(5+105);2= 55

Đáp số: 55

 BÀI TOÁN TÌM HAI SỐ KHI BIẾT TỔNG VÀ HIỆU

Ghi nhớ:

Số bé = (Tổng – Hiệu) : 2

Số lớn = (Tổng + Hiệu) : 2

Ví dụ. Tổng của hai số là 70. Hiệu của hai số là 10. Tìm hai số đó.

Bài giải

Số lớn là:

(70 + 10) : 2 = 40

Số bé là:

(70 – 10) : 2 = 30

Vậy số lớn 40; Số bé 30.

PHÂN SỐ

1. Phân số là gì ?

Mỗi phân số có tử số và mẫu số. Tử số là số tự nhiên viết trên gạch ngang. Mẫu số là số tự nhiên khác 0 viết dưới gạch ngang.

Ví dụ :$\frac{4}{5};\frac{7}{9}$

2. Tính cơ bản của phân số

2.1. Khi ta cùng nhân hoặc cùng chia cả tử và mẫu số của một phân số với cùng một số tự nhiên

lớn hơn 1, ta được một phân số mới bằng phân số ban đầu.

2.2. Vận dụng tính chất cơ bản của phân số:

a. Rút gọn phân số

$\frac{a}{b}=\frac{a:m}{b:m}=\frac{c}{d}$

 (m>1 , a và b phải cùng chia hết cho m )

 $\frac{c}{d}$ được gọi là phân số tối giản khi c và d chỉ cùng chia hết cho 1 (hay c và d  không cùng chia hết cho một số tự nhiên nào khác 1)

- Khi rút gọn phân số cần rút gọn đến phân số tối giản.

Ví dụ: Rút gọn phân số $\frac{54}{12}$ .

Hướng dẫn giải:

$\frac{54}{12}=\frac{54:6}{12:6}=\frac{9}{2}$

b. Quy đồng mẫu số - Quy đồng tử số:

* Quy đồng mẫu số 2 phân số: $\frac{a}{b}$ và $\frac{c}{d}$($b,d \ne 0)$ .

Ta có: $\frac{a}{b}=\frac{a\times d}{b\times d}$        $\frac{c}{d}=\frac{c\times b}{d\times b}$ 

Ví dụ: Quy đồng mẫu số 2 phân số $\frac{2}{7}$ và $\frac{3}{8}$ .

Hướng dẫn giải

$\frac{2}{7}=\frac{2\times 8}{7\times 8}=\frac{16}{56}$

$\frac{3}{8}=\frac{3\times 7}{8\times 7}=\frac{21}{56}$

Ví dụ: Quy đồng mẫu số 2 phân số $\frac{1}{3}$ và $\frac{5}{6}$

Hướng dẫn giải

Vì 6 : 3 = 2 nên $\frac{1}{3}=\frac{1\times 2}{3\times 2}=\frac{2}{6}$ .

II. Bốn phép tính với phân số

1. Phép cộng phân số

a. Cách cộng

* Cộng hai phân số cùng mẫu:  

$\frac{a}{b}+\frac{c}{b}=\frac{a+c}{b}(b\ne 0)$

Ví dụ: $\frac{3}{7}+\frac{2}{7}=\frac{3+2}{7}=\frac{5}{7}$

* Hai phân số khác mẫu số:

- Quy đồng mẫu số 2 phân số rồi đưa về trường hợp cộng 2 phân số có cùng mẫu số.

Ví dụ: $\frac{3}{5}+\frac{4}{3}=\frac{9}{15}+\frac{20}{15}=\frac{9+20}{15}=\frac{29}{15}$

* Cộng một số tự nhiên với một phân số.

- Viết số tự nhiên thành phân số có mẫu số bằng mẫu số của phân số đã cho.

- Cộng hai tử số và giữ nguyên mẫu số.

Ví dụ: $2+\frac{3}{4}=\frac{8}{4}+\frac{3}{4}=\frac{8+3}{4}=\frac{11}{4}$

b. Tính chất cơ bản của phép cộng

- Tính chất giao hoán:

$\frac{a}{b}+\frac{c}{d}=\frac{c}{d}+\frac{a}{b}$

- Tính chất kết hợp:

$(\frac{a}{b}+\frac{c}{d})+\frac{m}{n}=\frac{a}{b}+(\frac{c}{d}+\frac{m}{n})$

- Tổng của một phân số và số 0:

$\frac{a}{b}+0=0+\frac{a}{b}=\frac{a}{b}$

2. Phép trừ phân số

* Hai phân số cùng mẫu:

$\frac{a}{b}-\frac{c}{b}=\frac{a-c}{b}$

Ví dụ: $\frac{7}{9}-\frac{2}{9}=\frac{7-2}{9}=\frac{5}{9}$

* Hai phân số khác mẫu số: Quy đồng mẫu số 2 phân số rồi đưa về trường hợp trừ 2 phân số cùng mẫu số

Ví dụ: $\frac{3}{4}-\frac{1}{5}=\frac{15}{20}-\frac{4}{20}=\frac{11}{20}$

- Một phân số trừ đi số 0: $\frac{a}{b}-0=\frac{a}{b}$

Ví dụ:$\frac{4}{5}-0=\frac{4}{5}$

3. Phép nhân phân số

a. Cách nhân: $\frac{a}{b}\times \frac{c}{d}=\frac{a\times c}{b\times d}$

Ví dụ:$\frac{4}{5}\times \frac{2}{3}=\frac{4\times 2}{5\times 3}=\frac{8}{15}$

b. Tính chất cơ bản của phép nhân:

- Tính chất giao hoán: $\frac{a}{b}\times \frac{c}{d}=\frac{c}{d}\times \frac{a}{b}$

- Tính chất kết hợp: $(\frac{a}{b}\times \frac{c}{d})\times \frac{m}{n}=\frac{a}{b}\times (\frac{c}{d}\times \frac{m}{n})$

- Tính chất phân phối của phép nhân đối với phép cộng:

$(\frac{a}{b}+\frac{c}{d})\times \frac{m}{n}=\frac{a}{b}\times \frac{m}{n}+\frac{c}{d}\times \frac{m}{n}$

- Một hiệu 2 phân số nhân với một phân số: 

$(\frac{a}{b}-\frac{c}{d})\times \frac{m}{n}=\frac{a}{b}\times \frac{m}{n}-\frac{c}{d}\times \frac{m}{n}$

- Một phân số nhân với số 0: $\frac{a}{b}\times 0=0\times \frac{a}{b}=0$

- Muốn tìm giá trị phân số của một số ta lấy phân số nhân với số đó.

Ví dụ:

Tìm $\frac{1}{2}$ của 6 ta lấy $\frac{1}{2}\times 6=3$.

Tìm $\frac{1}{2}$ của $\frac{1}{3}$ ta lấy $\frac{1}{2}\times \frac{1}{3}=\frac{1}{6}$ .

4. Phép chia phân số

*) Cách chia:

$\frac{a}{b}:\frac{c}{d}=\frac{a}{b}\times \frac{d}{c}$=$\frac{a\times d}{b\times c}$

- Số 0 chia cho một phân số: 0:$\frac{a}{b}=0$

- Muốn tìm 1 số khi biết giá trị 1 phân số của nó ta lấy giá trị đó chia cho phân số tương ứng.

Ví dụ: Tìm số học sinh lớp 5A biết $\frac{2}{5}$ số học sinh của lớp 5A là 10 em.

Bài giải

Số học sinh của lớp 5A là:

 $10:\frac{2}{5}=25$(em)

III. So sánh phân số

1. So sánh phân số bằng cách quy đồng mẫu số, quy đồng tử số

a) Quy đồng mẫu số

Bước 1: Quy đồng mẫu số

Bước 2: So sánh phân số vừa quy đồng

Ví dụ: So sánh $\frac{1}{2}$ và $\frac{1}{3}$

Hướng dẫn giải

Ta có:

$\frac{1}{2}=\frac{1\times 3}{2\times 3}=\frac{3}{6}$

$\frac{1}{3}=\frac{1\times 2}{3\times 2}=\frac{2}{6}$

Vì $\frac{3}{6}>\frac{2}{6}$ nên $\frac{1}{2}>\frac{1}{3}$.

b) Quy đồng tử số

Bước 1: Quy đồng tử số

Bước 2: So sánh phân số đã quy đồng tử số

Ví dụ: So sánh hai phân số $\frac{2}{5}$ và $\frac{3}{4}$ bằng cách quy đồng tử số

Hướng dẫn giải

Ta có:

$\frac{2}{5}=\frac{2\times 3}{5\times 3}=\frac{6}{15}$

$\frac{3}{4}=\frac{3\times 2}{4\times 2}=\frac{6}{8}$

Vì$\frac{6}{15}<\frac{6}{8}$  nên $\frac{2}{5}<\frac{3}{4}$.

Vậy $\frac{2}{5}<\frac{3}{4}$ .

2. So sánh phân số với phân số trung gian

Nếu hai phân số $\frac{a}{b}$ và $\frac{c}{d}$ có a>c  và b

Khi chọn phân số trung gian ta có 2 cách chọn:

+ Cách 1: Chọn TS của phân số thứ nhất làm tử số của phân số trung gian và mẫu số của phân số thứ hai làm mẫu số của phân số trung gian.

+ Cách 2: Chọn tử số của phân số thứ hai làm TS của phân số trung gian và mẫu số của phân số thứ nhất làm MS của phân số trung gian.

Ví dụ: So sánh $\frac{15}{37}$ và $\frac{23}{31}$        

Hướng dẫn giải              

Chọn phân số trung gian: $\frac{15}{31}$

Vì $\frac{15}{37}<\frac{15}{31}$;$\frac{15}{31}<\frac{23}{31}$   nên $\frac{15}{37}<\frac{23}{31}$.

3. So sánh phần bù

Nếu hai phân số $\frac{a}{b}$ và $\frac{c}{d}$ mà b -a = d - c (hiệu mẫu số và tử số của hai phân số bằng nhau) thì ta so sánh phần bù.

 Ví dụ: $\frac{33}{35}$ và $\frac{45}{47}$

Hướng dẫn giải

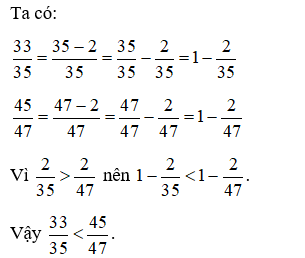
4.  So sánh phần thừa:

Nếu hai phân số $\frac{a}{b}$ và $\frac{c}{d}$  mà $a-b=c-d$  (hiệu giữa tử số và mẫu số của hai phân số bằng nhau) thì ta so sánh phần thừa.

Ví dụ: $\frac{79}{75}$ và $\frac{95}{91}$

Hướng dẫn giải

Ta thấy:

$\frac{79}{75}=\frac{75+4}{75}=1+\frac{4}{75}$

$\frac{95}{91}=\frac{91+4}{91}=1+\frac{4}{91}$

Vì $\frac{4}{75}>\frac{4}{91}$ nên 1+$\frac{4}{75}$> 1+ $\frac{4}{91}$ .

Vậy $\frac{79}{75}>\frac{95}{91}$.

GIỚI THIỆU TỈ SỐ

Ví dụ: Một đội xe có 5 xe tải và 7 xe khách

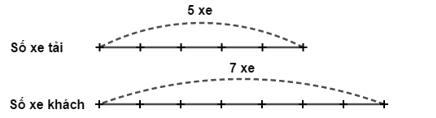
Ta nói:

- Tỉ số của số xe tải và số xe khách là 5 : 7 hay $\frac{5}{7}$ .

- Tỉ số này cho biết số xe tải bằng $\frac{5}{7}$ số xe khách.

- Tỉ số của số xe khách và số xe tải là 7 : 5 hay $\frac{7}{5}$ .

- Tỉ số này cho biết số xe khách bằng $\frac{7}{5}$ số xe tải.

Nhận xét: Tỉ số của a và b là a : b hay $\frac{a}{b}$ (b khác 0)

III. Bài toán Tìm hai số khi biết tổng và tỉ số của hai số đó

*) Các bước giải

Bước 1: Xác định tổng, xác định tỉ số và biểu diễn tổng, tỉ trên sơ đồ đoạn thẳng tóm tắt bài toán.

Bước 2: Theo sơ đồ để tìm tổng số phần bằng nhau

Bước 3: Tìm giá trị một phần

Bước 4: Tìm số lớn (hoặc số bé)

Bước 5: Tìm số bé (hoặc số lớn) và ghi đáp số

*) Ví dụ:

Tổng của hai số là 96. Tỉ số của hai số đó là $\frac{3}{5}$ . Tìm hai số đó.

Hướng dẫn giải

Ta có sơ đồ:

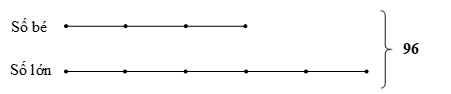
Tổng số phần bằng nhau là:

3 + 5 = 8 (phần)

Giá trị của một phần là:

96 : 8 = 12

Số bé là:

12 × 3 = 36

Số lớn là:

12 × 5 = 60

Đáp số: Số bé: 36, Số lớn: 60

4. Bài toán Tìm hai số khi biết hiệu và tỉ số của hai số đó.

*) Các bước giải

Bước 1: Xác định hiệu và tỉ của hai số đã cho trong đề bài và biểu thị trên sơ đồ đoạn thẳng tóm tắt bài toán.

Bước 2: Theo sơ đồ tìm hiệu số phần bằng nhau.

Bước 3: Tìm giá trị của một phần.

Bước 4: Tìm số bé ( hoặc số lớn).

Bước 5: Tìm số lớn (hoặc số bé) và đáp số.

*) Ví dụ

Hiệu của hai số là 24. Tỉ số của hai số đó là $\frac{3}{5}$ . Tìm hai số đó.

Bài giải

Ta có sơ đồ:

Hiệu số phần bằng nhau là:

5 – 3 = 2 (phần)

Giá trị của một phần là:

24 : 2 = 12

Số bé là:

12 × 3 = 36

Số lớn là:

12 × 5 = 60

Đáp số: Số lớn 60; Số bé 36

 TỈ LỆ BẢN ĐỒ

1) Tỉ lệ bản đồ là gì?

Tỉ lệ của bản đồ là tỉ số giữa một khoảng cách đo trên bản đồ và khoảng cách ngoài thực tế.

Ví dụ:

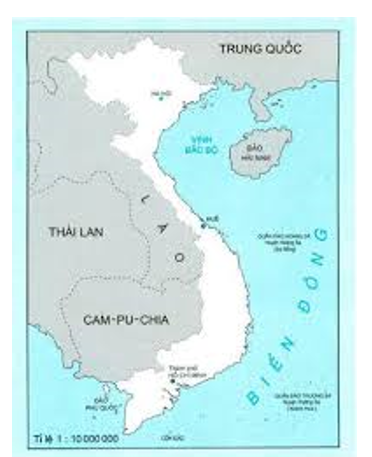
Ở góc dưới bản đồ của nước Việt Nam có ghi: Tỉ lệ 1 : 10 000 000. Tỉ lệ đó được gọi là tỉ lệ bản đồ.

Tỉ lệ 1 : 10 000 000 hay $\frac{1}{10 000 000}$ cho biết hình nước Việt Nam được vẽ thu nhỏ lại 10 000 000 lần. Chẳng hạn: Độ dài 1cm trên bản đồ ứng với độ dài thật là 10 000 000cm hay 100km.

Tỉ lệ bản đồ có thể được viết dưới dạng một phân số có tử số là 1.

Ví dụ: $\frac{1}{1000};\frac{1}{500};\frac{1}{1 000 000}$

2) Các dạng bài tập

2.1. Tính độ dài thật

Ví dụ. Trên bản đồ tỉ lệ 1: 1000000, quãng đường Hà Nội – Quảng Ninh đo được 112mm. Tìm độ dài thật của quãng đường Hà Nội – Quảng Ninh.

Bài giải

Quãng đường Hà Nội – Quảng Ninh dài là:

112 × 1000000 = 112 000 000 (mm)

Đổi: 112000000mm = 112km

Đáp số: 112km

2.2. Tính độ dài thu nhỏ trên bản đồ

Ví dụ. Quãng đường từ trung tâm Hà Nội đến Sơn Tây là 41km. Trên bản đồ tỉ lệ 1 : 1000000, quãng đường đó dài bài nhiêu mi-li-mét?

Bài giải

41km = 41000000mm

Trên bản đồ, quãng đường từ trung tâm Hà Nội đến Sơn Tây dài là:

41000000 : 1000000 = 41 (mm)

Đáp số: 41mm

Xem thêm các bài tổng hợp lý thuyết Toán lớp 4 đầy đủ, chi tiết khác:

Lý thuyết Biểu thức có chứa một chữ

Lý thuyết Các số có sáu chữ số

Lý thuyết Hàng và lớp. So sánh các số có nhiều chữ số

Lý thuyết Triệu và lớp triệu

Lý thuyết Viết số tự nhiên trong hệ thập phân