Đáp án cần chọn là: B

+ Hình thang là tứ giác có hai cạnh đối song song nên A đúng.

+ Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau nên B sai vì cạnh bên và cạnh đáy chưa chắc bằng nhau.

+ Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên song song và bằng nhau nên C đúng.

+ Hình thang vuông là hình thang có một góc vuông nên D đúng.

Đáp án cần chọn là: A

Theo định nghĩa: ”Hình thang là tứ giác có hai cạnh đối song song” nên A đúng.

Đáp án cần chọn là: D.

+ Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.

+ Trong hình thang cân, hai cạnh bên bằng nhau.

+ Trong hình thang cân, hai đường chéo bằng nhau.

Vậy cả A, B, C đều đúng

Đáp án cần chọn là: A

Vì tổng các góc của một tứ giác bằng $360°$ nên $\hat{A}+\hat{B}+\hat{C}+\hat{D}=360°$

$\Rightarrow \hat{A}=360°-80°-50°-100°=130°$

Đáp án cần chọn là: D

Vì tổng các góc của một tứ giác bằng $360°$ nên $\hat{A}+\hat{B}+\hat{C}+\hat{D}=360°$

$\Rightarrow \hat{A}=360°-70°-65°-115°=110°$

Đáp án cần chọn là: C

Vì tổng hai góc kề cạnh bên của hình thang bằng $180°$ nên góc kề còn lại của cạnh bên đó có số đo bằng $180°-70°=110°$.

Đáp án cần chọn là: D

Vì tổng hai góc kề cạnh bên của hình thang bằng $180°$ nên góc kề còn lại của cạnh bên đó có số đo bằng $180°-130°=50°$.

Đáp án cần chọn là: A

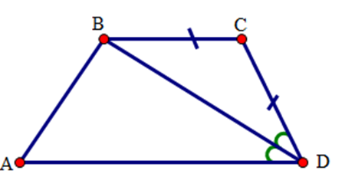
Xét ΔBCD có BC = CD (gt) nên ΔBCD là tam giác cân.

Suy ra $\widehat{CBD} = \widehat{CDB}.$

Vì DB là tia phân giác góc D của tứ giác ABCD nên $\widehat{ADB}=\widehat{CDB}$

Do đó $\widehat{CBD}=\widehat{ADB}$

Mà hai góc $\widehat{CBD}$  và $\widehat{ADB}$  là hai góc ở vị trí so le trong nên suy ra BC // AD.

Tứ giác ABCD có AD // BC (cmt) nên là hình thang.

Đáp án cần chọn là: D

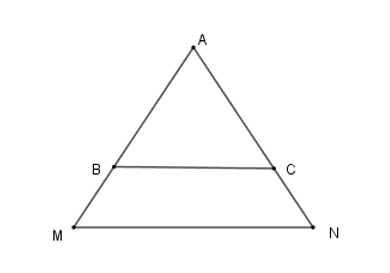
Xét ΔBAC có: BA = CA (gt) nên ΔBCA là tam giác cân.

Suy ra: $\widehat{CBA}=\widehat{ACB}=\frac{{180}^0-\hat{A}}{2}$(1) nên C đúng

Vì ΔAMN cân tại A => AM = AN mà AB = AC nên AM – AB = AN – AC ó MB = NC do đó A đúng.

Lại có: $\widehat{ANM}=\widehat{AMN}=\frac{{180}^0-\hat{A}}{2}$ (2) (do ΔAMN cân tại A)

Từ (1) và (2) suy ra: $\widehat{ABC}=\widehat{AMN}$

Mà hai góc $\widehat{ABC}$  và $\widehat{AMN}$  là hai góc ở vị trí đồng vị nên suy ra BC // MN

Tứ giác BCNM có: MN // BC (cmt) nên là hình thang.

Hình thang BCNM có: $\widehat{BMN}=\widehat{CNM}$ (cmt) nên là hình thang cân. Do đó, B đúng

Vậy cả A, B, C đúng

Đáp án cần chọn là: D

Từ B kẻ BH vuông góc với CD.

Tứ giác ABHD là hình thang có hai cạnh bên AD // BH nên AD = BH, AB = DH.

Mặt khác, AB = AD = 2cm nên suy ra BH = DH = 2cm.

Do đó: HC = DC – HD = 4 – 2 = 2cm.

Tam giác BHC có BH = HC = 2cm nên tam giác BHC cân đỉnh H.

Lại có $\widehat{BHC}=90°$ (do BH ⊥ CD) nên tam giác BHC vuông cân tại H.

Do đó $\widehat{BCH}=\left(180°-\widehat{BHC}\right)÷2=\left(180°-90°\right)÷2=45°$

Xét hình thang ABCD có:

$\widehat{ABC}=360°-\left(\hat{A}+\hat{D}+\hat{C}\right)=360°-\left(90°+90°+45°\right)=135°$

Vậy $\widehat{ABC}=135°$.

Đáp án cần chọn là: C

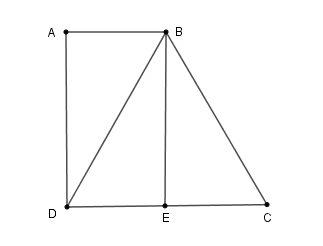
Từ B kẻ BE vuông góc với CD tại E.

Tứ giác ABED là hình thang có hai cạnh bên AD // BE nên AD = BE, AB = DE.

Mặt khác, DC = BC = 2AB nên DC = 2ED, do đó E là trung điểm của DC.

Xét ΔBDE và ΔBCE có $\widehat{BED}=\widehat{BEC}=90°$; DE = EC

BE cạnh chung nên ΔBED = ΔBEC (c – g – c)

Suy ra BD = BC mà BC = DC (gt) => BD = BC = CD nên ΔBCD đều.

Xét ΔBCD đều có BE là đường cao cũng là đường phân giác nên

$\widehat{EBC}=\frac{1}{2}\widehat{DBC}=\frac{1}{2}\times 60°=30°$

Vì AD // BE mà $\widehat{BAD}=90°$ nên  $\widehat{ABE}=180°-\widehat{BAD}=180°-90°=90°$ (hai góc trong cũng phía bù nhau)

Từ đó $\widehat{ABC}=\widehat{ABE}+\widehat{EBC}=90°+30°=120°$

Vậy $\widehat{ABC}=120°$

Tam giác ADE có AD = AE (gt) nên tam giác ADE cân tại A.

Suy ra $\widehat{ADE}=\widehat{AED}=\left(180°-\widehat{DAE}\right)÷2$ (1)

Tam giác ABC cân tại A (gt) nên $\widehat{ABC}=\widehat{ACB}=\left(180°-\widehat{BAC}\right)÷2$ (2)

Từ (1) và (2) suy ra $\widehat{ADE}=\widehat{ABC}$

Mà 2 góc này là hai góc ở vị trí đồng vị nên suy ra DE // BC

Tứ giác BDEC có DE // BC nên tứ giác BDEC là hình thang

Lại có $\widehat{ABC}=\widehat{ACB}$  (vì tam giác ABC cân tại A) nên BDEC là hình thang cân

Đáp án cần chọn là: C

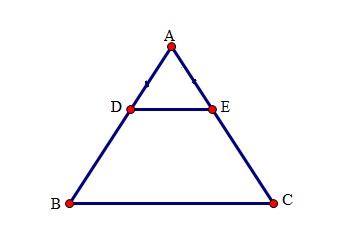
Tứ giác BDEC có DE // BC nên tứ giác BDEC là hình thang.

Lại có $\widehat{ABC}=\widehat{ACB}$  (vì tam giác ABC cân tại A) nên BDEC là hình thang cân

Đáp án cần chọn là: D

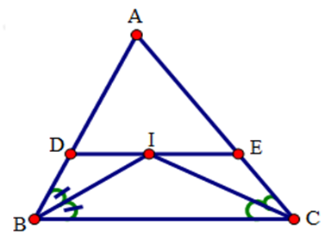
Xét tứ giác DECB có: DE // BC (gt) nên tứ giác DECB là hình thang.

Tương tự:

Tứ giác DICB có DI // BC (gt) nên tứ giác DICB là hình thang.

Tứ giác IECB có IE // CB (gt) nên tứ giác IECB là hình thang.

Đáp án cần chọn là: B

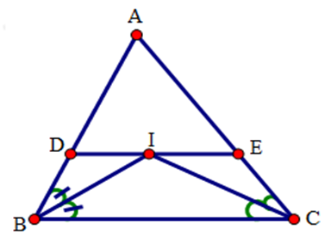
Vì DE // BC (gt) nên suy ra $\widehat{DIB}=\widehat{IBC}$  (so le trong)

Mà $\widehat{DBI}=\widehat{IBC}$ (gt) nên $\widehat{DIB}=\widehat{DBI}$

Suy ra tam giác BDI cân đỉnh D.

Do đó DI = DB (1)

Ta có: IE // CB nên suy ra $\widehat{EIC}=\widehat{BCI}$  (so le trong)

Mà $\widehat{ECI}=\widehat{BCI}$ (gt) nên $\widehat{ECI}=\widehat{EIC}$

Suy ra tam giác EIC cân đỉnh E

Do đó EI = EC (2)

Cộng (1) và (2) vế theo vế ta được: DI + EI = BD + CE

=> DE = BD + CE

Đáp án cần chọn là: C

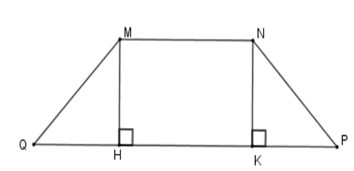
Kẻ MH ⊥ QP; NK ⊥ QP tại H, K => MH // NK

Tứ giác MNKH có MN // HK nên MNKH là hình thang, lại có MH // NK

=> MN = HK; MH = NK

(Vì hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau và hai cạnh đáy bằng nhau)

Lại có

MQ = NP (vì MNPQ là hình thang cân) suy ra ΔMQH = ΔNPK (ch – cgv)

=> QH = KP =  $\frac{QP-HK}{2}$

Mà HK = MN = 12 cm nên QH = KP = $\frac{40-12}{2}$  = 14 cm

Mà $\widehat{MQP}$  = $45°$ => ΔMHQ vuông cân tại H => MH = QH = 14 cm

Diện tích hình thang cân MNPQ là

S_MNPQ = $\frac{(MN+PQ).MH}{2}=\frac{(12+40).14}{2}$  = 364$c{m}^2$

Đáp án cần chọn là: B

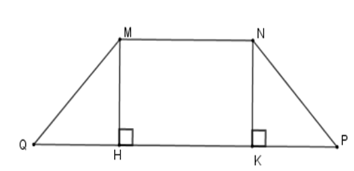
Kẻ MH ⊥ QP; NK ⊥ QP tại H, K => MH // NK

Tứ giác MNKH có MN // HK nên MNKH là hình thang, lại có MH // NK

=> MN = HK; MH = NK

(Vì hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau và hai cạnh đáy bằng nhau)

Lại có

MQ = NP (vì MNPQ là hình thang cân) suy ra ΔMQH = ΔNPK (ch – cgv)

=> QH = KP = $\frac{QP-HK}{2}$

Mà HK = MN = 8 cm nên QH = KP = $\frac{30-8}{2}$  = 11 cm

Mà $\widehat{MQP}$  = $45°$ => ΔMHQ vuông cân tại H => MH = QH = 11 cm

Diện tích hình thang cân MNPQ là

S_MNPQ = $\frac{(MN+PQ).MH}{2}=\frac{(8+30).11}{2}$ = 209$c{m}^2$.

Đáp án cần chọn là: B

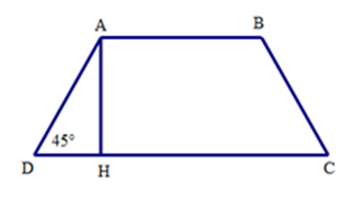
Ta có tam giác ADH vuông cân tại H vì $\hat{D}$  = 45⁰.

Do đó DH = AH = 6cm

Mà DH = $\frac{1}{2}$ (CD – AB)

Suy ra CD = 2DH + AB = 12 + 4 = 16 (cm)

Vậy CD = 16 cm.

Đáp án cần chọn là: A.

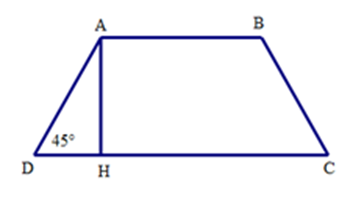
Ta có tam giác ADH vuông cân tại H vì $\hat{D}$  = $45°$.

Do đó DH = AH = 5cm

Mà DH = $\frac{1}{2}$ (CD – AB)

Suy ra CD = 2DH + AB = 2.5 + 3 = 13 (cm)

Vậy CD = 13 cm

Đáp án đúng là: B

Lời giải

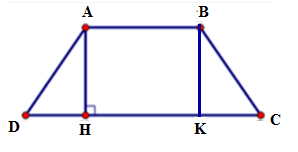
Kẻ BK ⊥ DC tại K.

Vì ABCD là hình thang cân nên ta có $\hat{D}=\hat{C}$; AD = BC

=> ΔAHD = ΔBKC (ch – gn) => DH = CK

Suy ra DH = $\frac{1}{2}$ (CD – AB)

Suy ra DH = $\frac{1}{2}$ (CD – AB) = $\frac{1}{2}$ (10 – 4) = 3 cm

Do ABCD là hình thang cân nên AD = BC = 5 cm

Áp dụng định lí Py-ta-go vào tam giác ADH vuông tại H ta có

$$\begin{gathered} A{D}^2=A{H}^2+D{H}^2 \\ \Rightarrow A{H}^2=A{D}^2-D{H}^2=5^2-3^2 = 16\Rightarrow AH=4 \end{gathered}$$

Vậy AH = 4cm.

*Phương pháp giải:

Sủ dụng tam giac bằng nhau để tính DH

Áp dụng định lí pytago để tính AH

*Lý thuyết:

1. Định lí Pytago:

Trong tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.

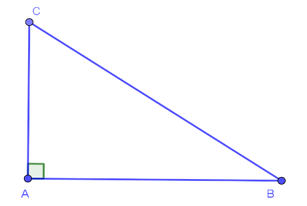
∆ABC vuông tại A: BC² = AB² + AC²

2. Định lí Pytago đảo:

Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.

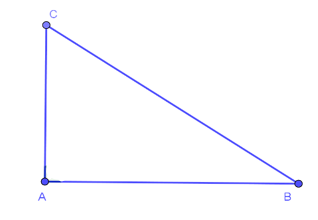
∆ABC có BC² = AB² + AC² thì ∆ABC vuông tại A

1. Hai tam giác bằng nhau:

Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.

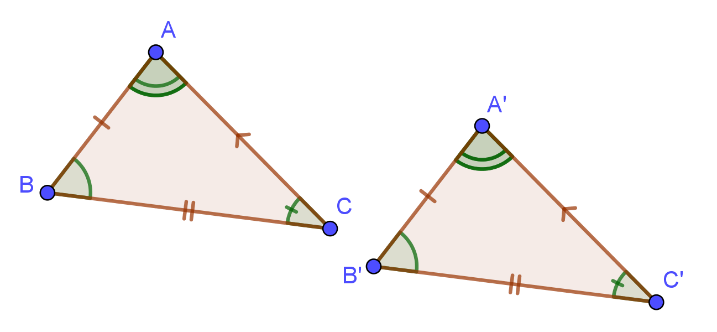
Hai tam giác ABC và A'B'C' bằng nhau ta viết $\Delta ABC=\Delta A\text{'}B\text{'}C\text{'}$

$\Delta ABC=\Delta A\text{'}B\text{'}C\text{'}$ nếu $\left\{\begin{array}{l}AB=A\text{'}B\text{'},BC=B\text{'}C\text{'},CA=C\text{'}A\text{'}.\\ \widehat{A}=\widehat{A\text{'}},\widehat{B}=\widehat{B\text{'}},\widehat{C}=\widehat{C\text{'}}.\end{array}\right.$

2. Các trường hợp bằng nhau của hai tam giác thường:

a. Trường hợp bằng nhau thứ nhất của hai tam giác: cạnh - cạnh - cạnh (c.c.c)

Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

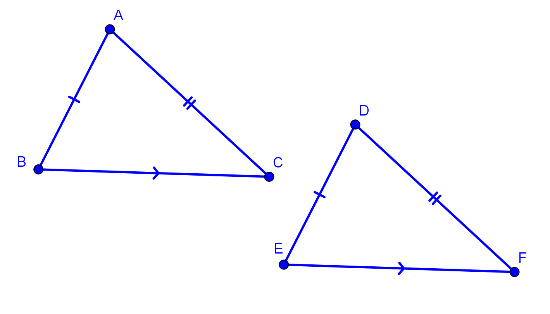
Hai tam giác ABC và DEF có: $\left\{\begin{array}{l}AB=DE\\ BC=\text{EF}\\ CA=FD\end{array}\right.$ thì $\Delta ABC=\Delta D\text{EF}$ (c.c.c)

b. Trường hợp bằng nhau thứ hai của hai tam giác: cạnh - góc - cạnh (c.g.c)

Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

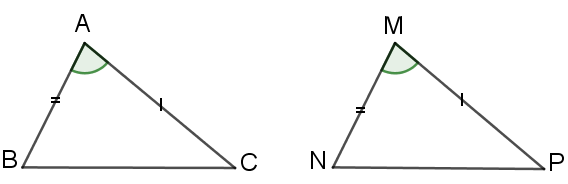
Hai tam giác ABC và MNP có:

$\left\{\begin{array}{l}AB=MN\\ \widehat{A}=\widehat{M}\\ AC=MP\end{array}\right.$ thì $\Delta ABC=\Delta MNP$(c.g.c)

*Hệ quả: Nếu hai cạnh góc vuông của hai tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thi hai tam giác vuông đó bằng nhau.

Xem thêm

Định lí Pi-ta-go và cách giải các dạng bài tập – Toán lớp 7 

Đáp án cần chọn là: C

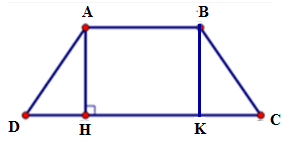
Ta có DH = $\frac{1}{2}$ (CD – AB) = $\frac{1}{2}$ (22 – 12) = 5 cm

Do ABCD là hình thang cân nên AD = BC = 13 cm

Áp dụng định lí Py-ta-go vào tam giác ADH vuông tại H ta có

$$\begin{gathered} A{D}^2=A{H}^2+D{H}^2 \\ \Rightarrow A{H}^2=A{D}^2-D{H}^2={13}^2-5^2=144\Rightarrow AH=12 \end{gathered}$$

Vậy AH = 12cm.

Đáp án cần chọn là: B

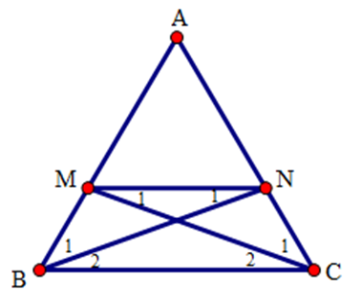
Ta có AB = AM + MB và AC = AN + NC

Mà AB = AC (do tam giác ABC cân tại A) và BM = NC (gt)

Suy ra AN = AM

Xét tam giác AMN cân tại A.

Suy ra $\widehat{AMN}=\widehat{ANM}$.

Xét tam giác ANM có: $\hat{A}+\widehat{AMN}+\widehat{ANM}=180°$ (tổng ba góc trong một tam giác)

 $\widehat{AMN}$ = $\frac{{180}^0-\hat{A}}{2}$(vì  $\widehat{AMN}=\widehat{ANM}$) (1)

Xét tam giác ABC cân tại A ta có:

$\hat{A}+\hat{B}+\hat{C}$ = $180°$ (tổng ba góc trong một tam giác) nên $\hat{B}$ = $\frac{{180}^0-\hat{A}}{2}$  (vì $\hat{B}=\hat{C}$ ) (2)

Từ (1) và (2) $\widehat{AMN}=\hat{B}$

Mà $\hat{B}$ , $\widehat{AMN}$  là hai góc đồng vị nên MN // BC

Xét tứ giác MNCB có MN // BC nên MNCB là hình thang.

Lại có $\hat{B}=\hat{C}$  (do ΔABC cân tại A) nên MNCB là hình thang cân.

Đáp án cần chọn là: A

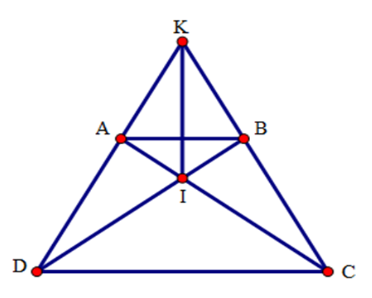
Xét tam giác ACD và tam giác BDC có:

+ AD = BC (do ABCD là hình thang cân)

+ AC = BD (do ABCD là hình thang cân)

+ CD là cạnh chung

Suy ra ΔACD = ΔBDC (c.c.c)

Suy ra $\widehat{ACD}=\widehat{BDC}$ , suy ra tam giác ICD cân tại I. Do đó ID = IC (1)

Tam giác KCD có hai góc ở đáy bằng nhau nên tam giác KCD cân ở K.

Do đó KC = KD (2)

Từ (1) và (2) suy ra KI là đường trung trực của CD (*).

Xét tam giác ADB và tam giác BCA có:

+ AD = BC (cmt)

+ AB là cạnh chung

+ AC = BD

Suy ra ΔADB = ΔBCA (c.c.c)

Suy ra $\widehat{ABD}=\widehat{BAC}$

Xét tam giác IAB có $\widehat{ABD}=\widehat{BAC}$  nên tam giác IAB cân tại I.

Do đó IA = IB (3)

Ta có KA = KD – AD; KB = KC – BC

Mà KD = KC, AD = BC, do đó KA = KB (4)

Từ (3) và (4) suy ra KI là đường trung trực của AB. (**)

Từ (*) và (**) suy ra KI là đường trung trực của hai đáy (đpcm)

Đáp án cần chọn là: C

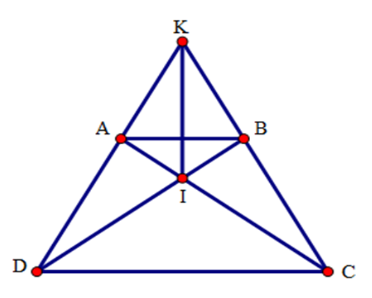
Xét tam giác ACD và tam giác BDC có:

+ AD = BC (do ABCD là hình thang cân)

+ AC = BD (do ABCD là hình thang cân)

+ CD là cạnh chung

Suy ra ΔACD = ΔBDC (c.c.c)

Suy ra $\widehat{ACD}=\widehat{BDC}$  (hai góc tương ứng), suy ra tam giác ICD cân tại I.

Nên C sai vì ta chưa đủ điều kiện để IC = CD

Tam giác KCD có hai góc ở đáy bằng nhau nên tam giác KCD cân ở K nên B đúng.

Xét tam giác KDI và tam giác KCI có:

+ KD = KC (do ΔKCD cân tại K))

+ KI là cạnh chung

+ IC = ID

Suy ra ΔKDI = ΔKCI (c.c.c)

Suy ra $\widehat{DKI}=\widehat{CKI}$ , do đó KI là phân giác $\widehat{AKB}$  nên D đúng.

Ta có AB // CD (do ABCD là hình thang) nên $\widehat{KAB}=\widehat{KDC}$; $\widehat{KBA}=\widehat{KCD}$  (các cặp góc đồng vị bằng nhau)

Mà $\widehat{KDC}=\widehat{KCD}$ (tính chất hình thang cân) nên $\widehat{KAB}=\widehat{KBA}$  (tính chất hình thang cân) nên ΔKAB cân tại K. Do đó A đúng

Đáp án cần chọn là: A

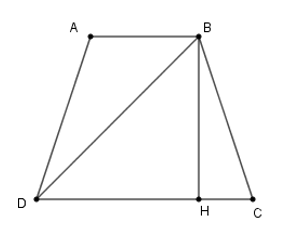
Kẻ BH ⊥ CD tại H.

Xét tam giác vuông BDH, theo định lý Pytago, ta có $B{D}^2=D{H}^2+B{H}^2$

Xét tam giác vuông CBH, theo định lý Pytago, ta có $B{C}^2=C{H}^2+B{H}^2$

Suy ra $B{D}^2-B{C}^2=\left(D{H}^2+B{H}^2\right)-\left(C{H}^2+B{H}^2\right)$

          $=D{H}^2-C{H}^2=\left(DH+CH\right)\times \left(DH-CH\right)=CD\times AB$

(do DH + CH = CD, DH - CH = AB)

Đáp án cần chọn là: B

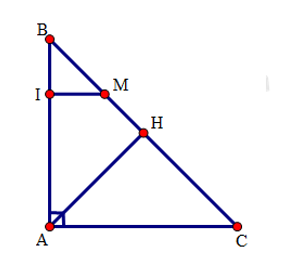
Tứ giác ACMI có: MI //AC (gt) và $\hat{A}=90°$ (gt) nên là hình thang vuông.