Cho hình thang cân ABCD đáy nhỏ AB = 4cm, đáy lớn CD = 10cm, cạnh bên BC = 5cm thì đường cao AH bằng:

Đáp án đúng là: B

Lời giải

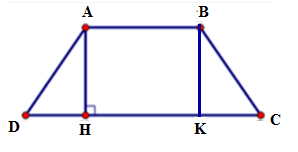
Kẻ BK ⊥ DC tại K.

Vì ABCD là hình thang cân nên ta có $\hat{D}=\hat{C}$; AD = BC

=> ΔAHD = ΔBKC (ch – gn) => DH = CK

Suy ra DH = $\frac{1}{2}$ (CD – AB)

Suy ra DH = $\frac{1}{2}$ (CD – AB) = $\frac{1}{2}$ (10 – 4) = 3 cm

Do ABCD là hình thang cân nên AD = BC = 5 cm

Áp dụng định lí Py-ta-go vào tam giác ADH vuông tại H ta có

$$\begin{gathered} A{D}^2=A{H}^2+D{H}^2 \\ \Rightarrow A{H}^2=A{D}^2-D{H}^2=5^2-3^2 = 16\Rightarrow AH=4 \end{gathered}$$

Vậy AH = 4cm.

*Phương pháp giải:

Sủ dụng tam giac bằng nhau để tính DH

Áp dụng định lí pytago để tính AH

*Lý thuyết:

1. Định lí Pytago:

Trong tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.

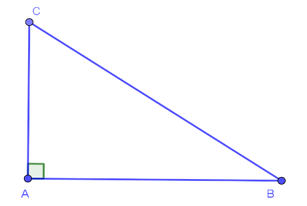
∆ABC vuông tại A: BC² = AB² + AC²

2. Định lí Pytago đảo:

Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.

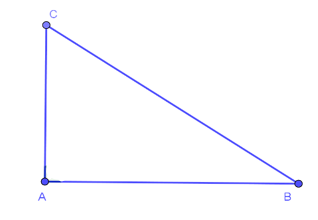
∆ABC có BC² = AB² + AC² thì ∆ABC vuông tại A

1. Hai tam giác bằng nhau:

Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.

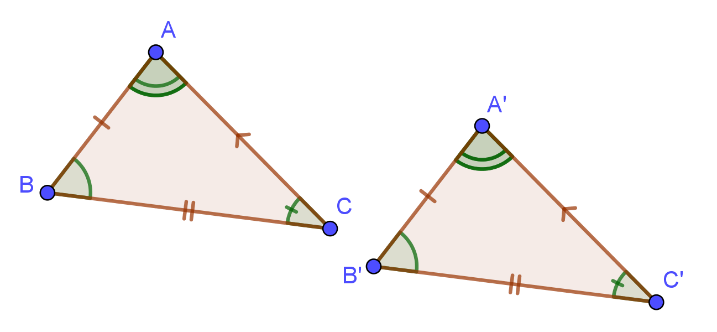
Hai tam giác ABC và A'B'C' bằng nhau ta viết $\Delta ABC=\Delta A\text{'}B\text{'}C\text{'}$

$\Delta ABC=\Delta A\text{'}B\text{'}C\text{'}$ nếu $\left\{\begin{array}{l}AB=A\text{'}B\text{'},BC=B\text{'}C\text{'},CA=C\text{'}A\text{'}.\\ \widehat{A}=\widehat{A\text{'}},\widehat{B}=\widehat{B\text{'}},\widehat{C}=\widehat{C\text{'}}.\end{array}\right.$

2. Các trường hợp bằng nhau của hai tam giác thường:

a. Trường hợp bằng nhau thứ nhất của hai tam giác: cạnh - cạnh - cạnh (c.c.c)

Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

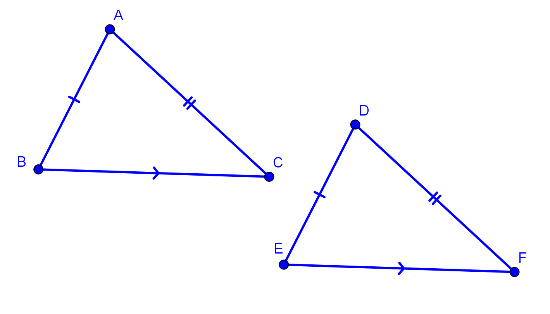
Hai tam giác ABC và DEF có: $\left\{\begin{array}{l}AB=DE\\ BC=\text{EF}\\ CA=FD\end{array}\right.$ thì $\Delta ABC=\Delta D\text{EF}$ (c.c.c)

b. Trường hợp bằng nhau thứ hai của hai tam giác: cạnh - góc - cạnh (c.g.c)

Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

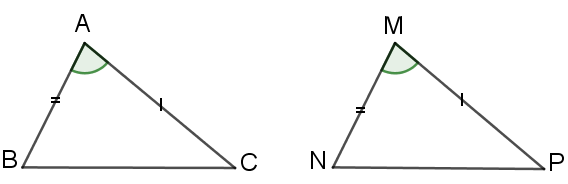
Hai tam giác ABC và MNP có:

$\left\{\begin{array}{l}AB=MN\\ \widehat{A}=\widehat{M}\\ AC=MP\end{array}\right.$ thì $\Delta ABC=\Delta MNP$(c.g.c)

*Hệ quả: Nếu hai cạnh góc vuông của hai tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thi hai tam giác vuông đó bằng nhau.

Xem thêm

Định lí Pi-ta-go và cách giải các dạng bài tập – Toán lớp 7 

Hai tam giác bằng nhau và các trường hợp bằng nhau của hai tam giác – Toán lớp 7