Trắc nghiệm Toán 8 Bài 7: Hình bình hành
-
805 lượt thi
-
25 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
23/07/2024Hãy chọn câu đúng. Tứ giác ABCD là hình bình hành nếu
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
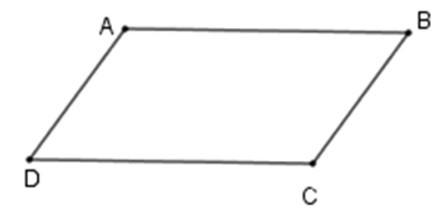
+ Tứ giác ABCD là hình bình hành khi AB // CD, BC // AD nên C sai.
+ Tứ giác ABCD là hình bình hành khi ; nên D đúng
+ A, B sai vì chưa đủ điều kiện để kết luận
Câu 2:
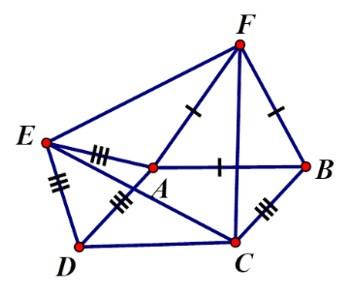
23/07/2024Cho hình bình hành ABCD có = α > 900. Ở phía ngoài hình bình hành vẽ các tam giác đều ADE, ABF. Tam giác CEF là tam giác gì? Chọn câu trả lời đúng nhất
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải


Câu 3:
15/07/2024Tính số đo các góc của hình bình hành ABCD biết = 300. Ta được:
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải

Câu 4:
04/09/2024Hãy chọn câu sai:
 Xem đáp án
Xem đáp án
Đáp án đúng là : B
*Lời giải
Dấu hiệu nhận biết:
+ Tứ giác có các cạnh đối song song là hình bình hành nên A đúng
+ Tứ giác có các cạnh đối bằng nhau là hình bình hành nên D đúng
+ Tứ giác có các góc đối bằng nhau là hình bình hành nên D đúng
Nhận thấy hình thang có hai góc kề một đáy bằng nhau là hình thang cân nên B sai
*Kiến thức liên quan:
Định nghĩa: Hình bình hành là tứ giác có các cạnh đối song song.
Tính chất:
Trong hình bình hành:
+ Các cạnh đối bằng nhau
+ Các góc đối bằng nhau
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường
Dấu hiệu nhận biết:
+ Tứ giác có các cạnh đối song song là hình bình hành
+ Tứ giác có các cạnh đối bằng nhau là hình bình hành.
+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+ Tứ giác có các góc đối bằng nhau là hình bình hành.
+ Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Chú ý: Hình bình hành là một hình thang đặc biệt (hình bình hành là hình thang có hai cạnh bên song song)
*Xem thêm các bài viết liên quan hay, chi tiết khác:
Lý thuyết Toán 8 Bài 12: Hình bình hành - Kết nối tri thức
Giải bài tập Toán 8 Bài 12: Hình bình hành
Câu 5:
23/07/2024Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở E, F. Chọn khẳng định đúng.
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
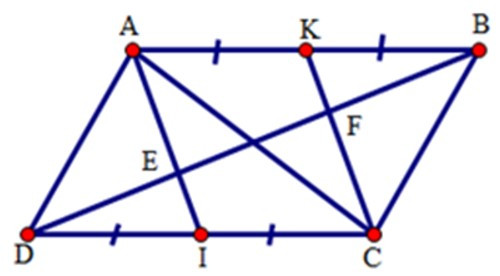
Vì AK = , IC = (gt)
mà AB = CD (cạnh đối hình bình hành) nên AK = IC
Vì AB // CD (gt), K Є AB, I Є DC => AK // IC
Tứ giác AKCI có AK // IC, AK = IC (cmt) nên là hình bình hành.
Suy ra AI // CK.
Mà E Є AI, F Є CK => EI // CF, KF // AE
Xét ΔDCF có: DI = IC (gt); IE // CF (cmt)
=> ED = FE (1)
Xét ΔABE có: AK = KB (gt), KF // AE (cmt)
=> EF = FB (2)
Từ (1) và (2) suy ra ED = FE = FB
Câu 6:
20/07/2024Điền cụm từ thích hợp vào chỗ trống: “Tứ giác có hai đường chéo … thì tứ giác đó là hình bình hành”.
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Dấu hiệu nhận biết:
Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
Câu 7:
21/07/2024Hãy chọn câu đúng. Tứ giác ABCD là hình bình hành nếu.
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
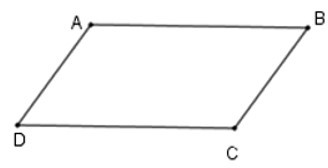
Tứ giác ABCD là hình bình hành khi AB = CD; AD = BC
Câu 8:
18/07/2024Hãy chọn câu sai.
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Trong hình bình hành:
+ Hình bình hành có các cạnh đối song song
+ Các cạnh đối bằng nhau
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường nên C sai
Câu 9:
21/07/2024Hãy chọn câu đúng. Cho hình bình hành ABCD, gọi E là trung điểm của AB, F là trung điểm của CD. Khi đó:
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
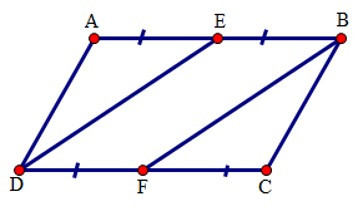
+ Vì ABCD là hình bình hành nên AB // CD; AB = CD
+ Xét tứ giác BEDF có BE =FD; BE // FD (do AB // CD) nên BDF là hình bình hành.
Từ đó: DE = BF (tính chất hình bình hành)
Câu 10:
23/07/2024Cho hình bình hành ABCD có . Số đo các góc của hình bình hành là:
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:

Câu 11:
23/07/2024Chọn câu sai. ABCD là hình bình hành. Khi đó:
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Trong hình bình hành:
+ Hình bình hành có các cạnh đối song song
+ Các cạnh đối bằng nhau
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường nên D sai
Câu 12:
15/07/2024Cho hình bình hành ABCD có . Số đo các góc của hình bình hành là:
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải

Câu 13:
19/07/2024Tính số đo các góc của hình bình hành ABCD biết = 400. Ta đươc:
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải

Câu 14:
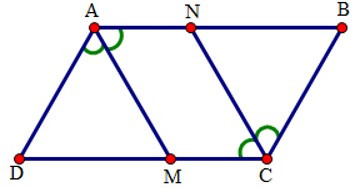
20/07/2024Cho hình bình hành ABCD. Tia phân giác của góc A cắt CD tại M.
Tia phân giác góc C cắt AB tại N (hình vẽ). Hãy chọn câu trả lời sai.
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải

Tứ giác AMCN có AN // CM, AM // CN (cmt) nên là hình bình hành (dấu hiệu nhận biết).
Vì AMCN là hình bình hành nên AN = CM (tính chất) nên A, D đúng.
Bì MC // AB => AMCB là hình thang nên B đúng.
Vì AN // CD => ANCD là hình thang
Chưa đủ điều kiện để ANCD là hình thang cân nên C sai.
Câu 15:
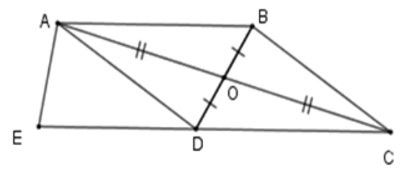
16/07/2024Hãy chọn câu trả lời sai.
Cho hình vẽ, ta có:
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
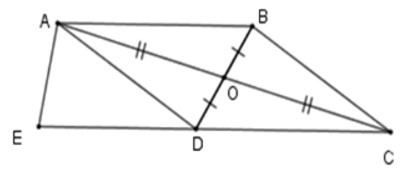
Từ hình vẽ ta có O là trung điểm của BD và AC. Do đó tứ giác ABCD có hai đường chéo AC vafBD cắt nhau tại trung điểm mỗi đường,
suy ra tứ giác ABCD là hình bình hành => A đúng
Vì ABCD là hình bình hành nên AB // CD; AD // BC (tính chất)
=> B, D đúng.
Chưa đủ điều điều kiện để ABCE là hình thang cân
Câu 16:
23/07/2024Hai góc kề nhau của một hình bình hành không thể có số đo là:
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Trong hình bình hành có các góc đối nhau và tổng các góc trong hình bình hành phải bằng 3600 nên ta có:
600.2 + 1200.2 = 3600
400.2 + 500.2 = 1800 ≠ 3600
1300.2 + 500.2 = 3600
1050.2 + 750.2 = 3600
Do đps hai góc kề của hình bình hành không thể có số đo 400; 500
Câu 17:
20/07/2024Cho tam giác ABC và H là trực tâm. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau ở D.
1. Chọn câu trả lời đúng nhất. Tứ giác BDCH là hình gì?
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
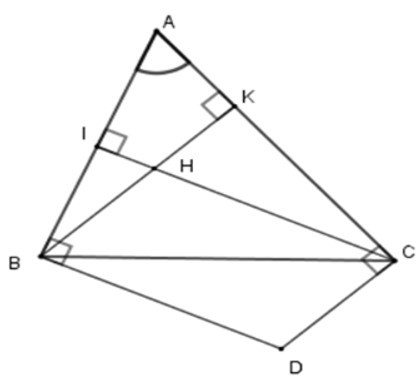
Gọi BK, CI là các đường cao của tam giác ABC.
Khi đó BK ⊥ AC; CI ⊥ AB hay BH ⊥ AC; CH ⊥ AB (vì H là trực tâm).
Lại có BD ⊥ AB; CD ⊥ AC (giả thiết) nên BD // CH (cùng vuông với AB)
và CD // BH (cùng vuông với AC)
Suy ra tứ giác BHCD là hình bình hành (dhnb)
Câu 18:
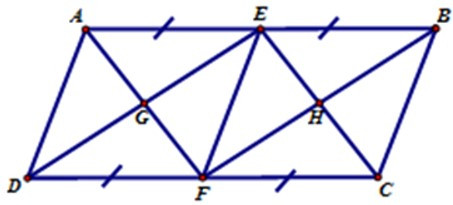
23/07/2024Hãy chọn câu đúng. Cho hình bình hành ABCD có các điều kiện như hình vẽ, trong hình có:
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
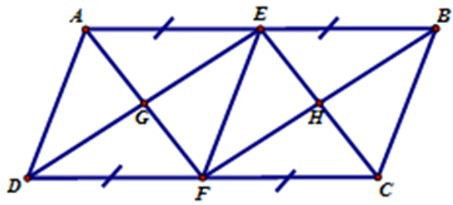
+ Vì ABCD là hình bình hành nên AB // CD, AD // BC
+ Xét tam giác AEFD có AE = FD; AE // FD
(do AB // CD) nên AEFD là hình bình hành.
+ Xét tứ giác BEFC có BE = FC; BE // FC
(do AB // CD) nên BEFC là hình bình hành
+ Xét tứ giác AECF có AE = FC; AE // FC
(do AB // CD) nên AEFC là hình bình hành
+ Xét tứ giác BEDF có BE = FD, BE //FD
(do AB // CD) nên BEDF là hình bình hành
+ Vì AECF là hình bình hành nên AF // EC
=> EH // GF; vì BEDF là hình bình hành
nên ED // BF => EG // HF
Suy ra EGHF là hình bình hành
Vậy có tất cả 6 hình bình hành: ABCD; AEFD; BEFC; AECF; BEDF; EGHF
Câu 19:
23/07/2024Cho tam giác ABC và H là trực tâm. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau ở D.
1. Chọn câu sai
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
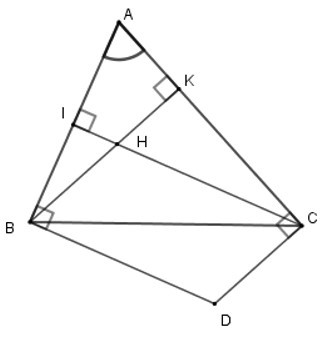
Gọi BK, CI là các đường cao của tam giác ABC.
Khi đó BK ⊥ AC; CI ⊥ AB hay BH ⊥ AC; CH ⊥ AB (vì H là trực tâm).
Lại có BD ⊥ AB; CD ⊥ AC (giả thiết) nên BD // CH (cùng vuông với AB)
và CD // BH (cùng vuông với AC)
Suy ra tứ giác BHCD là hình bình hành (dhnb)
Từ đó HB = CD; CH = BD nên D sai
(ta chưa đủ điều kiện để chỉ ra được HB = HC)
Câu 20:
22/07/2024Cho tứ giác ABCD. Gọi E, F lần lượt là giao điểm của AB và CD; M, N, P, Q lần lượt là trung điểm của AF, EC, BF, DE. Khi đó MNPQ là hình gì? Chọn đáp án đúng nhất.
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
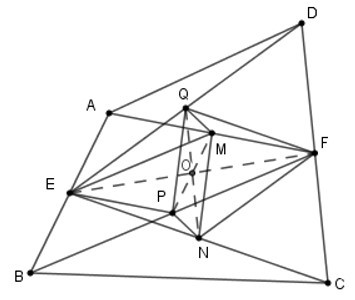
Nối EF; EP, FQ, EM, PM, QN. Gọi O là giao của QN và EF.
Xét tam giác CED có FN là đường trung bình nên
=> NFQE là hình bình hành nên hai đường chéo QN và EF giao nhau tại trung điểm của mỗi đường. Suy ra O là trung điểm của QN và EF (1)
Xét tam giác ABF có EM là đường trung bình nên
=> EMFB là hình bình hành nên hai đường chéo PM và EF giao nhau tại trung điểm của mỗi đường. Mà O là trung điểm của EF nên O cũng là trung điểm của PM (2)
Từ (1) và (2) suy ra: tứ giác QMNP có hai đường chéo QN, PM giao nhau tại trung điểm O mỗi đường nên QMNP là hình bình hành (dhnb)
Câu 21:
15/07/2024Tỉ số độ dài hai cạnh của hình bình hành là 3 : 5. Còn chu vi của nó bằng 48cm. Độ dài cạnh kề của hình bình hành là:
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Gọi độ dài hai cạnh của hình bình hành là a và b với a, b > 0
Theo bài ra ta có:
Nửa chu của hình bình hành là: 48 : 2 = 24cm
Suy ra: a + b = 24cm. Theo tính chất của dãy tỉ số bằng nhau ta có:
=> a = 3.3 = 9; b = 3.5 = 15
Vậy hai cạnh của hình bình hành là 9cm và 15cm
Câu 22:
20/07/2024Cho hình bình hành ABCD. Gọi E, F theo thứ tự là trung điểm của AD, BC. Đường chéo AC cắt BE, DF theo thứ tự ở K, I. Chọn khẳng định đúng nhất.
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
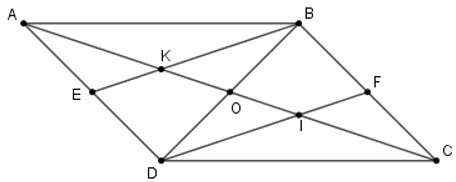
Gọi O là giao điểm của AC, BD
Vì ABCD là hình bình hành nên AC, BD giao nhau tại trung điểm O mỗi đường,
hay AO = CO =
Xét tam giác ABD có BE, AO là đường trung tuyến cắt nhau tại K nên K là trọng tâm ΔABD.
Suy ra AK = AO = AC = AC (1)
Xét tam giác CBD có DF, CO là hai đường trung tuyến cắt nhau tại I nên I là trọng tâm ΔCBD.
Suy ra CI = CO = AC = AC (2)
Lại có: AK + KI + CI + AC
=> KI = AC – AK – CI
= AC - AC - AC = AC (3)
Từ (1), (2) và (3) suy ra: AK = KI = IC
Câu 23:
22/07/2024Cho hình bình hành ABCD. Trên đường chéo BD lấy hai điểm E và F sao cho BE = DF < BD. Chọn khẳng định đúng.
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
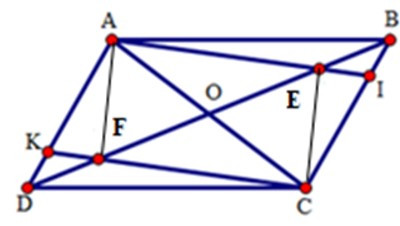
Gọi O là giao điểm của AC và BD.
Ta có OA = OC, OB = OD
Mà BE = DF (gt) => OE = FO.
Tứ giá AECF có hai đường chéo AC và EF cắt nhau tại trung điểm O
nên AECF là hình bình hành
=> FA = CE
Câu 24:
19/07/2024Cho tam giác ABC có BC = 6cm. Trên cạnh AB lấy các điểm D và E sao cho AD = BE. Qua D, E lần lượt vẽ các đường thẳng song song với BC, cắt AC theo thứ tự ở G và H. Tính tổng DG + EH.
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
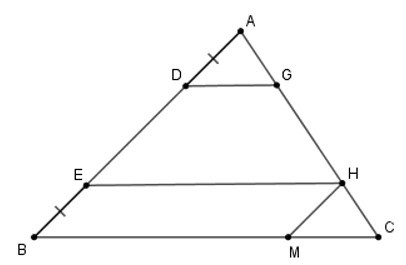
Kẻ HM // AM (M BC).
Xét tứ giác EHMB có MH // EB, EH // BM nên EHMB là hình bình hành.
Suy ra EH = BM; EB = HM (tính chất hình bình hành)
mà AD = BE => AD = MH
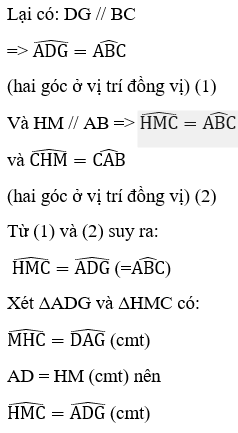
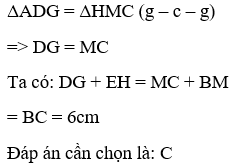
Câu 25:
23/07/2024Cho tứ giác ABCD. Gọi E, F lần lượt là giao điểm của AB và CD, AD và BC; M, N, P, Q lần lượt là trung điểm của AE, EC, CF, FA. Khi đó MNPQ là hình gì? Chọn đáp án đúng nhất
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
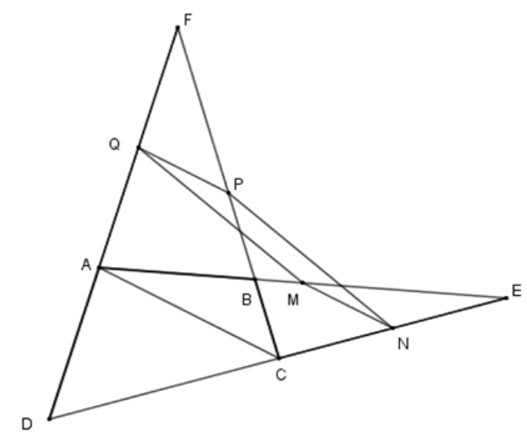
Nối AC. Vì M, N lần lượt là trung điểm của AE, EC nên MN là đường trung bình của
tam giác EAC suy ra MN // AC; MN = AC (1)
Tương tự PQ là đường trung bình của tam giác FAC
suy ra PQ // AC; PQ = AC (2)
Từ (1) và (2) suy ra PQ // NM; PQ = MN
nên MNPQ là hình bình hành (dhnb)
Có thể bạn quan tâm
- Trắc nghiệm Hình bình hành (có đáp án) (804 lượt thi)
- Bài tập Hình bình hành (có lời giải chi tiết) (253 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Tứ giác có đáp án (Nhận biết) (693 lượt thi)
- Trắc nghiệm Hình thang cân (có đáp án) (597 lượt thi)
- Trắc nghiệm Tứ giác có đáp án (Thông hiểu) (450 lượt thi)
- Trắc nghiệm Đường trung bình của tam giác, của hình thang (có đáp án) (416 lượt thi)
- Trắc nghiệm Hình thoi (có đáp án) (410 lượt thi)
- Trắc nghiệm Tứ giác (có đáp án) (397 lượt thi)
- Trắc nghiệm Hình thoi có đáp án (Thông hiểu) (397 lượt thi)
- Trắc nghiệm Tứ giác có đáp án (Vận dụng) (387 lượt thi)
- Trắc nghiệm Đường thẳng song song với một đường thẳng cho trước (có đáp án) (386 lượt thi)
- Trắc nghiệm Hình thang (có đáp án) (364 lượt thi)
