Câu hỏi:
22/07/2024 320Cho tứ giác ABCD. Gọi E, F lần lượt là giao điểm của AB và CD; M, N, P, Q lần lượt là trung điểm của AF, EC, BF, DE. Khi đó MNPQ là hình gì? Chọn đáp án đúng nhất.
A. Hình bình hành
B. Hình thang vuông
C. Hình thang cân
D. Hình thang
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án: A
Giải thích:
Lời giải
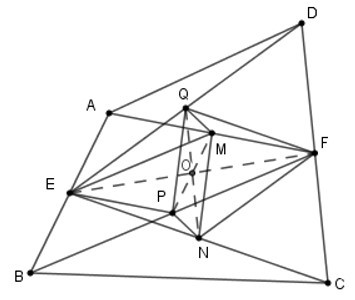
Nối EF; EP, FQ, EM, PM, QN. Gọi O là giao của QN và EF.
Xét tam giác CED có FN là đường trung bình nên
=> NFQE là hình bình hành nên hai đường chéo QN và EF giao nhau tại trung điểm của mỗi đường. Suy ra O là trung điểm của QN và EF (1)
Xét tam giác ABF có EM là đường trung bình nên
=> EMFB là hình bình hành nên hai đường chéo PM và EF giao nhau tại trung điểm của mỗi đường. Mà O là trung điểm của EF nên O cũng là trung điểm của PM (2)
Từ (1) và (2) suy ra: tứ giác QMNP có hai đường chéo QN, PM giao nhau tại trung điểm O mỗi đường nên QMNP là hình bình hành (dhnb)
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 5:
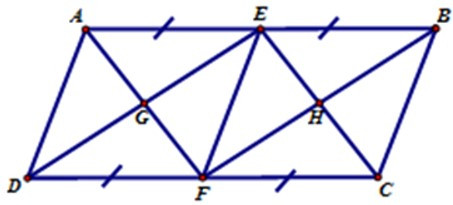
Hãy chọn câu đúng. Cho hình bình hành ABCD có các điều kiện như hình vẽ, trong hình có:
Câu 7:
Cho hình bình hành ABCD có . Số đo các góc của hình bình hành là:
Câu 8:
Cho tam giác ABC có BC = 6cm. Trên cạnh AB lấy các điểm D và E sao cho AD = BE. Qua D, E lần lượt vẽ các đường thẳng song song với BC, cắt AC theo thứ tự ở G và H. Tính tổng DG + EH.
Câu 9:
Cho tứ giác ABCD. Gọi E, F lần lượt là giao điểm của AB và CD, AD và BC; M, N, P, Q lần lượt là trung điểm của AE, EC, CF, FA. Khi đó MNPQ là hình gì? Chọn đáp án đúng nhất
Câu 10:
Điền cụm từ thích hợp vào chỗ trống: “Tứ giác có hai đường chéo … thì tứ giác đó là hình bình hành”.
Câu 11:
Cho hình bình hành ABCD. Trên đường chéo BD lấy hai điểm E và F sao cho BE = DF < BD. Chọn khẳng định đúng.
Câu 13:
Cho tam giác ABC và H là trực tâm. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau ở D.
1. Chọn câu trả lời đúng nhất. Tứ giác BDCH là hình gì?
Câu 14:
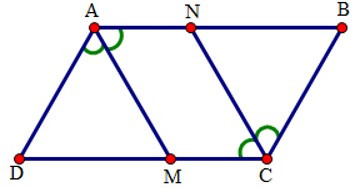
Cho hình bình hành ABCD. Tia phân giác của góc A cắt CD tại M.
Tia phân giác góc C cắt AB tại N (hình vẽ). Hãy chọn câu trả lời sai.
Câu 15:
Cho tam giác ABC và H là trực tâm. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau ở D.
1. Chọn câu sai











