Trắc nghiệm Toán 8 Bài 11: Hình thoi
-
410 lượt thi
-
23 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
21/07/2024Hình thoi không có tính chất nào dưới đây?
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Hình thoi có tất cả các tính chất của hình bình hành
+ Các cạnh đối song song và bằng nhau, các góc đối bằng nhau
+ Hai đường chéo giao nhau tại trung điểm mỗi đường.
Ngoài ra còn có
+ Hai đường chéo vuông góc với nhau
+ Hai đường chéo là các đường phân giác của các góc của hình thoi
Câu 2:
23/07/2024Hãy chọn câu sai.
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
+ Tứ giác có 4 cạnh bằng nhau là hình thoi
+ Hình bình hành có hai cạnh kề bằng nhau là hình thoi
+ Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi
+ Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi
Nên A, C, D đúng, B sai
Câu 3:
16/07/2024Điền cụm từ thích hợp vào chỗ trống: “Hình thoi có hai đường chéo …”
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Hình thoi có tất cả các tính chất của hình bình hành:
+ Các cạnh đối song song và bằng nhau, các góc đối bằng nhau.
+ Hai đường chéo giao nhau tại trung điểm mỗi đường.
Ngoài ra còn có:
+ Hai đường chéo vuông góc với nhau
+ Hai đường chéo là các đường phân giác của các góc của hình thoi
Câu 4:
19/07/2024Điền từ thích hợp vào chỗ trống: “Tứ giác có hai đường chéo … là hình thoi”
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
+ Tứ giác có hai đường chéo giao nhau tại trung điểm mỗi đường là hình thoi
+ Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi
Nên tứ giác có hai đường chéo giao nhau tại trung điểm mỗi đường và vuông góc với nhau là hình thoi
Câu 5:
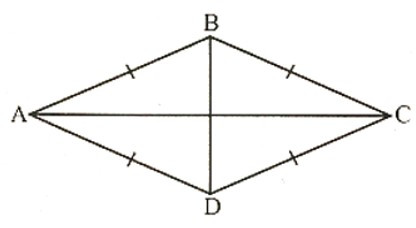
19/07/2024Tứ giác dưới đây là hình thoi theo dấu hiệu nào?
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Tứ giác có 4 cạnh bằng nhau là hình thoi nên A đúng.
Câu 6:
15/07/2024Hình thoi có chu vi bằng 20cm thì độ dài cạnh của nó bằng
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Gọi cạnh của hình thoi là a cm (a > 0)
Vì hình thoi có 4 cạnh bằng nhau nên chu vi hình thoi
là 4a = 20 a = 5cm
Vậy cạnh hình thoi có độ dài là 5cm
Câu 7:
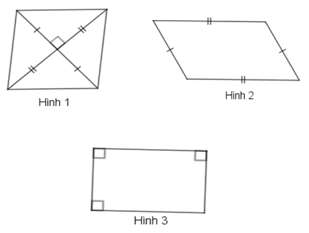
18/07/2024Cho các hình sau, chọn khẳng định đúng.
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Hình 1 là hình thoi vì có hai đường cheo giao nhau tại trung điểm mỗi đường và vuông góc với nhau
Hình 2 không là hình thoi vì bốn cạnh không bằng nhau
Hình 3 không là hình thoi vì bốn cạnh không bằng nhau
Câu 8:
21/07/2024Hình thoi có chu vi bằng 36cm thì độ dài cạnh của nó bằng
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Gọi cạnh của hình thoi là a cm (a > 0)
Vì hình thoi có 4 cạnh bằng nhau nên chu vi hình thoi
là 4a = 36 a = 9cm
Vậy cạnh hình thoi có độ dài là 9cm
Câu 9:
18/07/2024Cho hình thoi có độ dài hai đường chéo là 24cm và 10cm. Tính độ dài cạnh hình thoi.
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
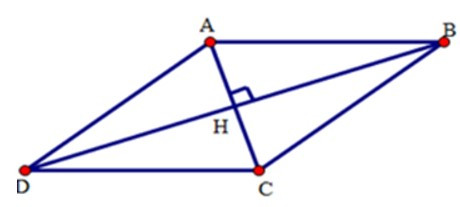
Giả sử ABCD là hình thoi có hai đường chéo cắt nhau tại H
và AC =10cm, BD = 24cm
Do ABCD là hình thoi nên:
AC ⊥ BD;
AH = AC = .10 = 5 (cm);
HB = BD = .24 = 12 (cm)
Xét tam giác AHB vuông tại H ta có:
AB2 = AH2 + HB2
= 52 + 122 = 25 + 144 = 169
Suy ra AB = 13cm
Câu 10:
22/07/2024Cho hình thoi ABCD. Trên các cạnh BC và CD lần lượt lấy hai điểm E và F sao cho BE = DF. Gọi G, H thứu tự là giao điểm của AE, AF với đường chéo BD.
1. Tứ giác AGCH là hình gì?
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
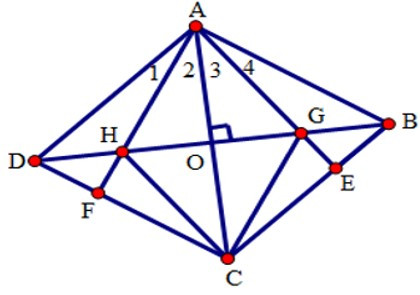
Gọi O là giao điểm của AC và BD thì AC ⊥ BD
(do O là giao điểm của hai đường chéo của hình thoi)
Áp dụng định nghĩa, tính chất về góc và giả thiết vào hình thoi ABCD, ta được:
AB = AD, ; BE = DF
Từ đó suy ra ΔABE = ΔADF (c.g.c)
Suy ra (hai góc tương ứng).
Mà AC là phân giác của => (1)
Do đó AO là phân giác của .
Xét tam giác AGH có AO là đường cao, đồng thời là đường phân giác nên tam giác AGH cân tại A.
Suy ra HO = OG (2)
Do ABCD là hình thoi nên AO = OC (tính chất đường chéo của hình thoi) (3)
Từ (1), (2), (3) suy ra: AHCG là hình thoi.
Câu 11:
17/07/2024Cho hình thoi ABCD. Trên các cạnh BC và CD lần lượt lấy hai điểm E và F sao cho BE = DF. Gọi G, H thứu tự là giao điểm của AE, AF với đường chéo BD.
Cho OC = 4; OH = 3. Tính chu vi tứ giác AHCG
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
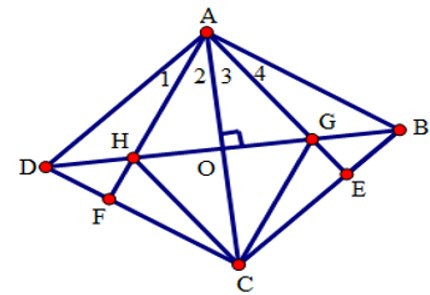
Vì OC = 4; OH = 3 nên
CH = (định lý Pytago)
Vì AHCG là hình thoi (theo câu trước) nên chu vi tứ giác AHCG
bằng 4.CH = 4.5 = 20cm.
Câu 12:
23/07/2024Cho hình thoi ABCD có chu vi bằng 16cm, đường cao AH bằng 2cm. Tính các góc của hình thoi. Hãy chọn câu đúng.
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
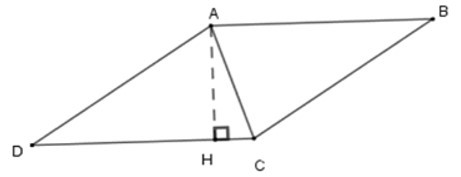
Vì chu vi hinh thoi là 16cm nên cạnh hình thoi có độ dài 16 : 4 = 4cm.
Suy ra AD = 4cm
Xét tam giác AHD vuông tại H có

Câu 13:
17/07/2024Cho hình thoi có độ dài hai đường chéo là 12cm và 16cm. Tính độ dài cạnh hình thoi.
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
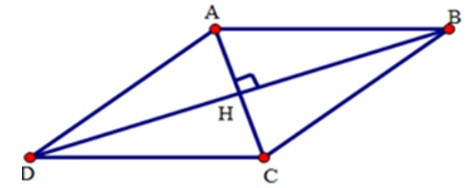
Giả sử ABCD là hình thoi có hai đường chéo cắt nhau tại H và AC =12cm, BD = 16cm
Do ABCD là hình thoi nên:
AC ⊥ BD;
AH = AC = .12 = 6 (cm);
HB = BD = .16 = 8 (cm)
Xét tam giác AHB vuông tại H ta có:
AB2 = AH2 + HB2 = 62 + 82
= 36 + 64 = 100
Suy ra AB = 10cm
Câu 14:
15/07/2024Cho tam giác ABC vuông ở A, trung tuyến AM. Gọi D là trung điểm của AB, M’ là điểm đối xứng với M qua D.
1. Tứ giác AMBM’ là hình gì?
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
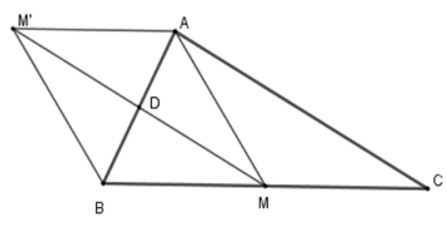
Vì M’ đối xứng M qua D nên DM = DM’ (1)
M, D lần lượt là trung điểm của BC, AB nên MD là đường trung bình của ΔABC.
Suy ra MD // AC (2)
Mặt khác ΔABC vuông ở A nên AB ⊥ AC (2)
Từ (1) và (2) suy ra DM ⊥ AB
=> MM’ ⊥ AB.
Vì D là trung điểm của AB (gt) và D là trung điểm của MM’
nên tứ giác AMBM’ là hình bình hành. Mặt khác MM’ ⊥ AB nên AMBM’ là hình thoi.
Câu 15:
22/07/2024Cho hình thoi ABCD có chu vi bằng 24 cm,đường cao AH bằng 3cm. Tính .
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
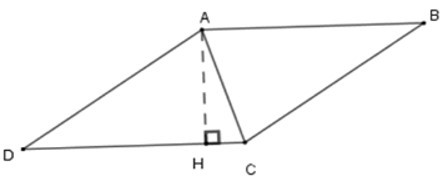


Câu 16:
20/07/2024Cho hình bình hành ABCD. Gọi E, F là trung điểm của các cạnh AD và BC. Các đường BE, DE cắt các đường chéo AC tại P và Q. Tứ giác EPFQ là hình thoi nếu góc ACD bằng:
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
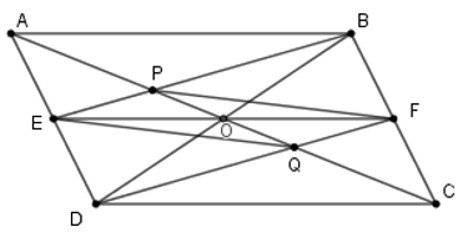
Gọi O là giao điểm của hai đường chéo AC và BD
Vì ABCD là hình bình hành nên O là trung điểm của AC, BD.
Xét tứ giác EDFB có nên EDFB là hình bình hành suy ra
Xét tam giác ABD có P là giao điểm hai đường trung tuyến
nên P là trọng tâm ΔABD
=> EP = BE
Xét tam giác CBD có Q là giao điểm hai đường trung tuyến nên Q là
trọng tâm ΔCBD
=> QF = DF
Mà BE = DF (cmt) => EP = QF
Xét tứ giác EPFQ có
=> EPQF là hình bình hành
Để hình bình hành EPFQ là hình thoi thì EF ⊥ PQ.
Mà EF // CD (do E là trung điểm AD, F là trung điểm BC)
Nên PQ ⊥ CD hay AC ⊥ CD
=> = 900.
Câu 17:
20/07/2024Cho hình thang ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Hình thang ABCD có thêm điều kiện gì thì MNPQ là hình thoi. Hãy chọn câu đúng.
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
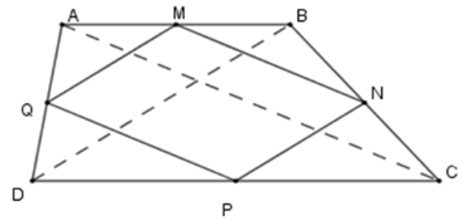
+ Xét tam giác ABC có MN là đường trung bình
nên MN // AC; MN = AC (1)
Tương tự ta có PQ là đường trung bình tam giác ADC
nên PQ // AC; PQ = AC (2)
Từ (1) và (2) suy ra MN // PQ; MN = PQ
=> MNPQ là hình bình hành
Để hình bình hành MNPQ là hình thoi ta cần có MN = MQ
Mà MN = AC (cmt); MQ = BD (do MQ là đường trung bình tam giác ABD)
Suy ra AC = BD
Vậy để hình bình hành MNPQ là hình thoi thì AC = BD
Câu 18:
18/07/2024Cho tứ giác ABCD. Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA. Các đường chéo AC, BD của tứ giác ABCD phải có điều kiện gì thì EFGH là hình thoi?
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
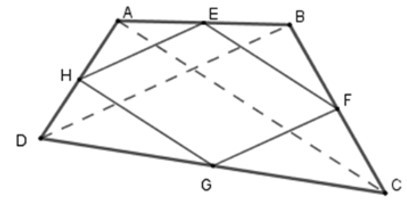
Vì E, F lần lượt là trung điểm của AB, BC nên EF là đường trung bình của ΔABC. Suy ra EF // AC và EF = AC. (1)
Tương tự ta có: HG // AC và HG = AC. (2)
Từ (1) và (2) suy ra tứ giác EFGH là hình bình hành.
Muốn cho tứ giác EFGH là hình thoi thì nó cần phải có thêm hai cạnh kề bằng nhau.
Nên EH = EF AC = BD
Câu 19:
15/07/2024Tứ giác ABCD có AB = CD. Gọi M, N theo thứ tự là trung điểm của BC, AD. Gọi I, K theo thứ tự là trung điểm của AC, BD. Chọn câu đúng nhất.
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
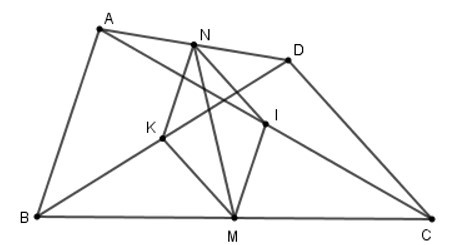
Từ giả thiết ta có: KM, IM, IN, KN lần lượt là các đường trung bình của các tam giác BCD, CAB, ADC, DBA (định nghĩa đường trung bình).
Đặt BA = CD = 2a.
Áp dụng định lý đường trung bình và giả thiết vào bốn tam giác trên ta được:
MK = CD = a; IM = AB = a;
NI = CD = a; KN = BA = a
Suy ra MK = KN = NI = IM.
Tứ giác KMIN có bốn cạnh bằng nhau nên là hình thoi.
Áp dụng tính chất về đường chéo vào hình thoi KMIN ta được: MN ⊥ KI;
MN là đường phân giác .
Câu 20:
17/07/2024Cho tứ giác ABCD có = 500, = 800, AD = BC. Gọi E, F lần lượt là trung điểm của các cạnh AB và CD. Tính số đo góc EFC.
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
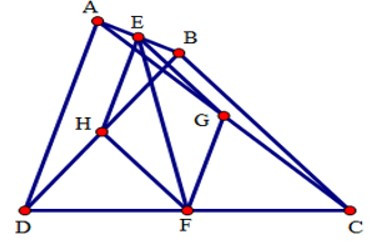
Gọi G, H lần lượt là trung điểm của AC, BD.
Vì E, G lần lượt là trung điểm của AB, AC nên EG là đường trung bình của tam giác ABC. Suy ra EG = BC, EG // BC.
Chứng minh tương tự ta cũng có:
GF = AD, FH = BC, HE = AD;
GF // AD; FH // BC; HE // AD
Mà AD = BC (gt),
nên EG = GF = FH = HE
Suy ra: tứ giác EGFH là hình thoi.
Suy ra EF là tia phân giác của góc

Câu 21:
23/07/2024Cho tam giác ABCD. Trên các cạnh AB và AC lần lượt lấy hai điểm D và E sao cho BD = CE. Gọi M, N, P, Q thứ tự là trung điểm của BE, CD, DE và BC. Chọn câu đúng nhất.
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
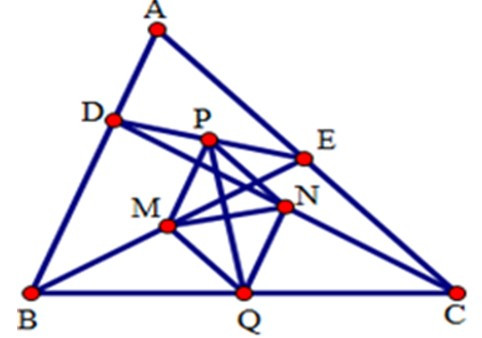
Từ giả thiết ta có MP, NP, NQ, QM lần lượt là các đường trung bình của các tam giác BDE, ECD, DCB, BEC (định nghĩa đường trung bình).
Đặt BD = CE = 2a
Áp dụng định lý đường trung bình và giả thiết vào bốn tam giác trên ta được:
MP = BD = a; NQ = BD = a;
NP = CE = a; MQ = CE = a.
Suy ra MN = NP = PQ = QM
Tứ giác MNPQ có bốn cạnh bằng nhau nên là hình thoi.
Áp dụng tính chất về đường chéo vào hình thoi MNPQ ta được: MN ⊥ PQ
Câu 22:
18/07/2024Cho hình thoi ABCD có góc A tù. Biết đường cao kẻ từ đỉnh A đến cạnh CD chia đôi cạnh đó. Tính các góc của hình thoi.
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
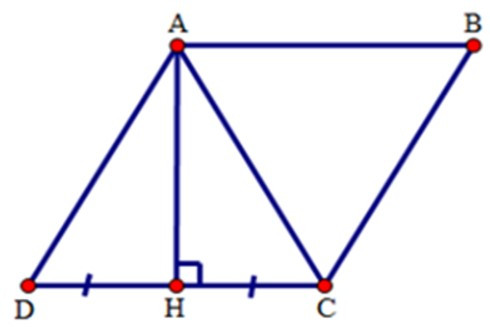
Gọi H là chân đường cao kẻ từ A đến canh CD. Từ giả thiết ta có: AH ⊥ DC, CH = HD suy ra AH là đường trung trực của đoạn CD nên AC = CD. (1)
Do ABCD là hình thoi nên AD = CD (2)
Từ (1) và (2) suy ra AD =CD = AC nên tam giác ACD là tam giác đều,
do đó = 600.
Vì góc A và góc D là hai góc trong cùng phía của AB // CD nên chúng bù nhau
hay 1800 – 600 = 1200.
Áp dụng tính chất về góc vào hình thoi ta được:
= 600, = 1200
Câu 23:
19/07/2024Cho tam giác ABC đều, H là trực tâm, đường cao AD. M là điểm bất kì trên cạnh BC. Gọi E, F lần lượt là hình chiếu của M trên AB, AC, gọi I là trung điểm của đoạn thẳng AM. ID cắt EF tại K.
Chọn câu sai.
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
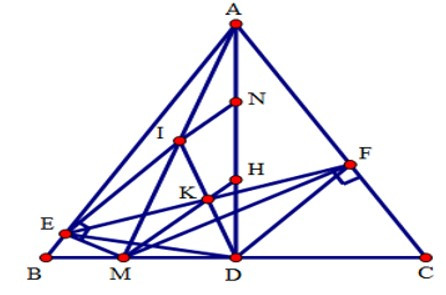
Tam giác EAM vuông tại E, EI là đường trung tuyến nên: EI = IM = IA = AM.
Từ EI = IA suy ra tam giác IAE cân tại I, từ đó có:
(góc ngoài của tam giác).
Chứng minh tương tự với tam giác vuông ADM ta có:
= 2, DI = AM.
Do đó: EI = DI ( = AM);
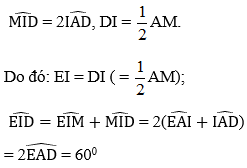
Tam giác IED cân (vì EI = DI) có: = 600 nên là tam giác đều, từ đó EI = ED = ID.
Tương tự tam giác IDF đều suy ra: ID = DF = IF.
Do đó EI = ED = DF = IF. Suy ra tứ giác EIFD là hình thoi.
Suy ra K là trung điểm chung của EF và ID.
Gọi N là trung điểm của AH.
Tam giác ABC đều có H là trực tâm của tam giác ABC nên H cũng là trọng tâm tam giác.
Do đó AN = NH = HD.
Ta có: MH // IN (vì IN là đường trung bình của tam giác AMH)
và KH // IN (vì KH là đường trung bình của tam giác DIN).
Từ H ta chỉ vẽ được một đường thẳng song song với IN (tiên đề Ơ – clit)
nên M, H, K thẳng hang.
Vậy D sai vì ID = IF.
Có thể bạn quan tâm
- Trắc nghiệm Hình thoi (có đáp án) (409 lượt thi)
- Thi Online Bài tập Hình thoi (có lời giải chi tiết) (271 lượt thi)
- Trắc nghiệm Hình thoi có đáp án (Nhận biết) (296 lượt thi)
- Trắc nghiệm Hình thoi có đáp án (Thông hiểu) (397 lượt thi)
- Trắc nghiệm Hình thoi có đáp án (Vận dụng) (308 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Hình bình hành (có đáp án) (804 lượt thi)
- Trắc nghiệm Tứ giác có đáp án (Nhận biết) (692 lượt thi)
- Trắc nghiệm Hình thang cân (có đáp án) (597 lượt thi)
- Trắc nghiệm Tứ giác có đáp án (Thông hiểu) (450 lượt thi)
- Trắc nghiệm Đường trung bình của tam giác, của hình thang (có đáp án) (416 lượt thi)
- Trắc nghiệm Tứ giác (có đáp án) (396 lượt thi)
- Trắc nghiệm Tứ giác có đáp án (Vận dụng) (387 lượt thi)
- Trắc nghiệm Đường thẳng song song với một đường thẳng cho trước (có đáp án) (386 lượt thi)
- Trắc nghiệm Hình thang (có đáp án) (364 lượt thi)
- Trắc nghiệm Hình vuông có đáp án (Thông hiểu) (340 lượt thi)
