Câu hỏi:
23/07/2024 245Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở E, F. Chọn khẳng định đúng.
A. DE = FE; FE > FB
B. DE = FE = FB
C. DE > FE; EF = FB
D. DE > FE > FB
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án: B
Giải thích:
Lời giải
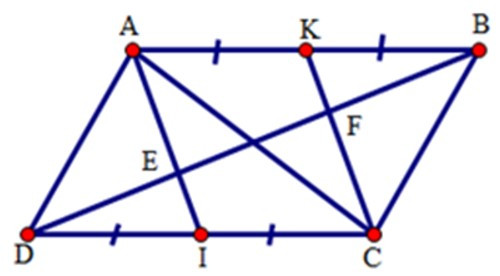
Vì AK = , IC = (gt)
mà AB = CD (cạnh đối hình bình hành) nên AK = IC
Vì AB // CD (gt), K Є AB, I Є DC => AK // IC
Tứ giác AKCI có AK // IC, AK = IC (cmt) nên là hình bình hành.
Suy ra AI // CK.
Mà E Є AI, F Є CK => EI // CF, KF // AE
Xét ΔDCF có: DI = IC (gt); IE // CF (cmt)
=> ED = FE (1)
Xét ΔABE có: AK = KB (gt), KF // AE (cmt)
=> EF = FB (2)
Từ (1) và (2) suy ra ED = FE = FB
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 5:
Hãy chọn câu đúng. Cho hình bình hành ABCD có các điều kiện như hình vẽ, trong hình có:
Câu 7:
Cho hình bình hành ABCD có . Số đo các góc của hình bình hành là:
Câu 8:
Cho tam giác ABC có BC = 6cm. Trên cạnh AB lấy các điểm D và E sao cho AD = BE. Qua D, E lần lượt vẽ các đường thẳng song song với BC, cắt AC theo thứ tự ở G và H. Tính tổng DG + EH.
Câu 9:
Cho tứ giác ABCD. Gọi E, F lần lượt là giao điểm của AB và CD, AD và BC; M, N, P, Q lần lượt là trung điểm của AE, EC, CF, FA. Khi đó MNPQ là hình gì? Chọn đáp án đúng nhất
Câu 10:
Điền cụm từ thích hợp vào chỗ trống: “Tứ giác có hai đường chéo … thì tứ giác đó là hình bình hành”.
Câu 11:
Cho hình bình hành ABCD. Trên đường chéo BD lấy hai điểm E và F sao cho BE = DF < BD. Chọn khẳng định đúng.
Câu 13:
Cho tam giác ABC và H là trực tâm. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau ở D.
1. Chọn câu trả lời đúng nhất. Tứ giác BDCH là hình gì?
Câu 14:
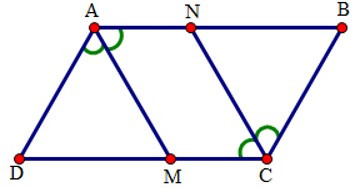
Cho hình bình hành ABCD. Tia phân giác của góc A cắt CD tại M.
Tia phân giác góc C cắt AB tại N (hình vẽ). Hãy chọn câu trả lời sai.
Câu 15:
Cho tam giác ABC và H là trực tâm. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau ở D.
1. Chọn câu sai











