Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0o đến 150o có đáp án (Thông hiểu)
Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0o đến 150o có đáp án (Thông hiểu)
-
402 lượt thi
-
11 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
08/01/2025Rút gọn biểu thức A=cot2x−cos2xcot2x+sinx.cosxcotx
Xem đáp án
Đáp án đúng: A
*Lời giải:
A=cot2x−cos2xcot2x+sinx.cosxcotx=1−cos2xcot2x+sinx.cosxcotx=1−sin2x+sin2x=1
*Phương pháp giải:
biến đổi biểu thức đã cho để thu được kết quả rút gọn
*Một số dạng bài thêm về giá trị lượng giác của một góc bất kì từ 0 đến 180:
Tính chất:
Hai góc bù nhau là hai góc có tổng bằng 180o. Cho góc α ta có:
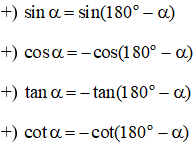
Hai góc phụ nhau là hai học có tổng bằng 90o. Cho góc α ta có:
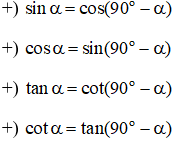
Các dạng bài.
Dạng 1: Góc và dấu của các giá trị lượng giác.
Phương pháp giải:
Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất và bảng giá trị lượng giác đặc biệt và các chú ý về dấu của giá trị lượng giác liên quan tới góc.
Dạng 2: Cho một giá trị lượng giác, tính các giá trị lượng giác còn lại.
Phương pháp giải:
Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác để từ một giá trị lượng giác suy ra các giá trị lượng giác còn lại.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết giá trị lượng giác của một góc bất kì từ 0 đến 180 và cách giải bài tập chi tiết nhất
Giải Toán 10 Bài 5 (Kết nối tri thức): Giá trị lượng giác của một góc từ 0 độ đến 180 độ
Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ có đáp án – Toán lớp 10
Câu 2:
14/07/2024Tính giá trị biểu thức P=cos300cos600−sin300sin600
Xem đáp án
Đáp án D
Vì 30∘ và 60∘ là hai góc phụ nhau nên {sin300=cos600sin600=cos300
⇒P=cos300cos600−sin300sin600=P=cos300cos600−cos600cos300=0
Câu 3:
17/07/2024Giá trị của biểu thức A=sin2510+sin2550+sin2390+sin2350 là:
Xem đáp án
Đáp án D
A=(sin2510+sin2390)+(sin2550+sin2350)=(sin2510+cos2510)+(sin2550+cos2550)=2
Câu 4:
19/07/2024Cho cotα=13. Giá trị của biểu thức A=3sinα+4cosα2sinα−5cosα là:
Xem đáp án
Đáp án D
Ta có:
A=3sinα+4sinαcotα2sinα−5sinαcotα=3+4cotα2−5cotα=13
Câu 5:
21/07/2024Cho hai góc nhọn α và β (α < β). Khẳng định nào sau đây là sai?
Xem đáp án
Đáp án A
Vì 0∘<α<β<90∘ nên:
0 < sin α < sin β, cos α > cos β > 0
0 < tan α < tan β, cot α > cot β > 0
Câu 6:
18/07/2024Cho ΔABC vuông tại A, góc B bằng 30∘. Khẳng định nào sau đây là sai?
Xem đáp án
Đáp án A
Ta có: cosB=cos300=√32
Câu 7:
14/07/2024Cho ΔABC vuông tại A, góc C bằng 30∘. Khẳng định nào sau đây là sai?
Xem đáp án
Đáp án A
Ta có: sinC=sin300=12 nên A sai
Câu 8:
21/07/2024Cho biết cosα=−23 và 900<α<1800. Tính tanα?
Xem đáp án
Đáp án D
Do 900<α<1800
Ta có: 1+tan2α=1cos2α
⇔tan2α=54⇒tanα=−√52
Câu 9:
20/07/2024Cho biết sinα3=35. Giá trị của P=3sin2α3+5cos2α3 bằng bao nhiêu?
Xem đáp án
Đáp án B
Ta có biểu thức:
sin2α3+cos2α3=1⇔cos2α3=1−sin2α3=1625
Do đó ta có:
P=3sin2α3+5cos2α3=3.(35)2+5.1625=10725
Câu 10:
13/07/2024Cho biết tanα=−3. Giá trị của P=6sinα−7cosα6cosα+7sinα bằng bao nhiêu?
Xem đáp án
Đáp án B
Ta có:
P=6sinα−7cosα6cosα+7sinα=6sinαcosα−76+7sinαcosα=6tanα−76+7tanα=53
Câu 11:
12/07/2024Giá trị của biểu thức A=tan10tan20tan30...tan880tan890 là:
Xem đáp án
Đáp án D
A=(tan10tan890).(tan20.tan880)...(tan440.tan460).tan450=(tan10.cot10).(tan20.cot20)....(tan440.cot440).tan450=1.1....1.1=1