Bài tập về Tính đơn điệu của hàm số có lời giải (Đề 1)
-
721 lượt thi
-
26 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 6:
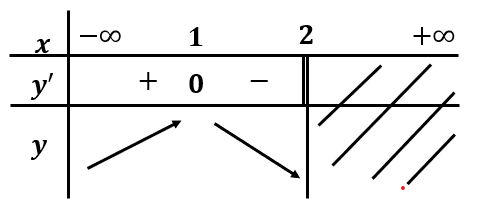
23/07/2024Hỏi hàm số nghịch biến trên các khoảng nào ?
Xem đáp án
Hàm số nghịch biến trên các khoảng (-4;-1) và (-1;2)
Câu 15:
15/10/2024Cho các hàm số sau:
Hỏi hàm số nào nghịch biến trên toàn trục số?
Xem đáp án
*Phương pháp giải:
Dựa vào tính đơn điệu của hàm số: Cho hàm số y = f(x) xác định trên K. Khi đó:
Hàm số nghịch biến trên K ⇔ f'(x) ≤ 0, ∀ x ∈ K
Hàm số đồng biến trên K ⇔ f'(x) ≥ 0, ∀ x ∈ K
Ghi nhớ: f'(x) = 0 chỉ tại một số hữu hạn điểm hoặc vô hạn điểm rời rạc trên K.
Chú ý:
Nếu đồ thị hàm f'(x) nằm bên dưới Ox trên khoảng K ⇒ f'(x) < 0; ∀ x ∈ K nên hàm f(x) nghịch biến trên K.
Nếu đồ thị hàm f'(x) nằm bên trên Ox trên khoảng K ⇒ f'(x) > 0; ∀ x ∈ K nên hàm f(x) đồng biến trên K.
*Lời giải:
*Một số lý thuyết liên quan:
Phương pháp giải chung
Bước 1. Tìm tập xác định D.
Bước 2. Tính đạo hàm y’ = f'(x). Tìm các giá trị xi (i=1, 2, .., n) mà tại đó f'(x) = 0 hoặc f'(x) không xác định.
Bước 4. Sắp xếp các giá trị xi theo thứ tự tăng dần và lập bảng biến thiên.
Bước 5. Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số và chọn đáp án chính xác nhất.
Chú ý:
• Đối với hàm phân thức hữu tỉ thì dấu “=” khi xét dấu đạo hàm y' không xảy ra.
• Giả sử:
+ Hàm số đồng biến trên R
+ Hàm số nghịch biến trên R
Trường hợp 2 thì hệ số c khác 0 vì khi a = b = c = 0 thì f(x) = d
(Đường thẳng song song hoặc trùng với trục Ox thì không đơn điệu)
Xem thêm các bài viết liên quan hay, chi tiết:
Trắc nghiệm Sự đồng biến, nghịch biến của hàm số có đáp án (P1) (Vận dụng)
Toán 12 Bài 1: Sự đồng biến, nghịch biến của hàm số
Cách xét tính đồng biến, nghịch biến của hàm số (2024) chi tiết nhất
đồng biến trên tập xác định của nó.
đồng biến trên R.
. Khẳng định nào sau đây là khẳng định đúng?
Câu 26:
21/07/2024Bất phương trình có tập nghiệm (a;b]. Hỏi hiệu b-a có giá trị là bao nhiêu?
Xem đáp án
Điều kiện
bất phương trình
Đặt f(t) = với mọi t
hàm f(t) đồng biến trên
tập nghiệm của bất phương trình là (2;3]