Toán 12 Bài 1: Sự đồng biến, nghịch biến của hàm số

Mục lục Giải Toán 12 Bài 1: Sự đồng biến, nghịch biến của hàm số

Hoạt động 1 trang 4 Toán lớp 12 Giải tích:Từ đồ thị (H.1, H.2) hãy chỉ ra các khoảng tăng, giảm của hàm số y = cosx trên đoạn $\left[-\frac{\pi }{2};\frac{3\pi }{2}\right]$ và của hàm số y = |x| trên khoảng $\left(-\infty ;+\infty \right).$

Lời giải:

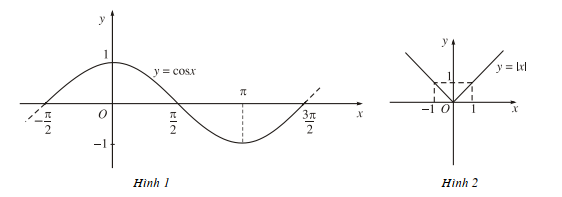
+ Hình 1: Hàm số y = cosx trên đoạn $\left[-\frac{\pi }{2};\frac{3\pi }{2}\right]$:

- Các khoảng tăng:$\left[-\frac{\pi }{2};0\right]$ , $\left[\pi ;\frac{3\pi }{2}\right]$ (do đồ thị hàm số đi lên trong các khoảng đó, nghĩa là khi x tăng thì y cũng tăng).

- Khoảng giảm: [0; π] (do đồ thị hàm số đi xuống trong khoảng đó, nghĩa là khi x tăng thì y giảm).

+ Hình 2: Hàm số y = |x| trên khoảng $\left(-\infty ;+\infty \right):$

- Khoảng tăng: [0; +∞) (do đồ thị hàm số đi lên trong khoảng đó, nghĩa là khi x tăng thì y cũng tăng).

- Khoảng giảm (– ∞, 0] (do đồ thị hàm số đi xuống trong khoảng đó, nghĩa là khi x tăng thì y giảm).

Hoạt động 2 trang 5, 6 Toán lớp 12 Giải tích: Xét các hàm số sau và đồ thị của chúng:

a) $y=-\frac{x^2}{2}$ (H.4a)

b) $y=\frac{1}{x}$ (H.4b)

Xét dấu đạo hàm của mỗi hàm số và điền vào bảng tương ứng. Từ đó hãy nêu nhận xét về mối quan hệ giữa sự đồng biến, nghịch biến của hàm số và dấu của đạo hàm.

Lời giải:

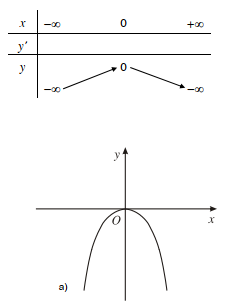
a) Hàm số $y=-\frac{x^2}{2}$ có đạo hàm

y' = - x, y' = 0 khi x = 0.

Trên khoảng $\left(-\infty ;0\right)$, đạo hàm y' mang dấu +, đồ thị hàm số đi lên; trên khoảng $\left(0;+\infty \right)$, đạo hàm mang dấu –, đồ thị hàm số đi xuống. Ta có bảng biến thiên như sau:

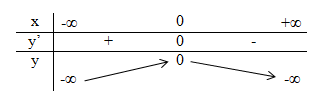
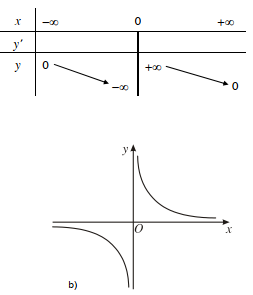
b) Hàm số $y=\frac{1}{x}$ xác định trên

có đạo hàm là $y^{\text{'}}=\frac{-1}{x^2}<0$
với mọi $x\in ℝ\backslash \left\{0\right\}$.

Do đó, trên các khoảng $\left(-\infty ;0\right),\left(0;+\infty \right)$, đạo hàm y' đều mang dấu –, đồ thị hàm số đi xuống. Ta có bảng biến thiên như sau:

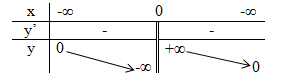
* Nhận xét: Cho hàm số y = f(x) có đạo hàm trên K.

+ Nếu f'(x) > 0 với mọi x thuộc K thì hàm số f(x) đồng biến trên K.

+ Nếu f'(x) < 0 với mọi x thuộc K thì hàm số f(x) nghịch biến trên K.

Bài 1 trang 9 Toán 12 Giải tích: Xét sự đồng biến, nghịch biến của các hàm số:

a) y = 4 + 3x – x²;

b) $y=\frac{1}{3}{x}^3+3x^2-7x-2$;

c) y = x⁴ – 2x² + 3;

d) y = – x³ + x² – 5.

Lời giải:

a) Tập xác định : D = $ℝ$

Ta có: y' = 3 – 2x

y’ = 0 $\iff$ 3 – 2x = 0$\iff x=\frac{3}{2}$ 

Ta có bảng biến thiên:

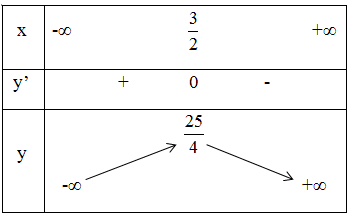
Vậy hàm số đồng biến trong khoảng $\left(-\infty ;\frac{3}{2}\right)$ và nghịch biến trong khoảng $\left(\frac{3}{2};+\infty \right).$

b) Tập xác định : D = $ℝ$

Ta có: y' = x² + 6x - 7

y' = 0 $\iff x^2+6x-7=0\iff \left[\begin{array}{l}x=-7\\ x=1\end{array}\right.$ 

Ta có bảng biến thiên:

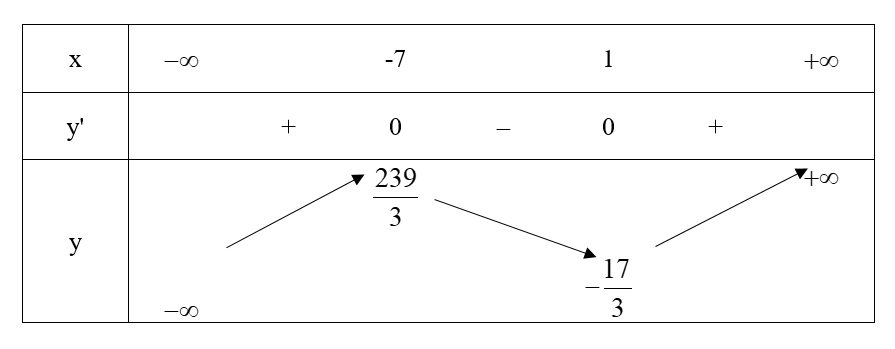
Vậy hàm số đồng biến trong các khoảng (-∞ ; -7) và (1 ; +∞); nghịch biến trong khoảng (-7; 1).

c) Tập xác định: D = $ℝ$

Ta có: y' =  4x³ – 4x

y' = 0$\iff$4x³ – 4x = 0

$\iff$ 4x.(x – 1)(x + 1) = 0

$\iff \left[\begin{array}{l}x=0\\ x=1\\ x=-1\end{array}\right.$

Bảng biến thiên:

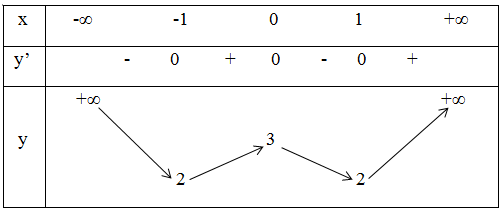
Vậy hàm số nghịch biến trong các khoảng (-∞ ; -1) và (0 ; 1); đồng biến trong các khoảng (-1 ; 0) và (1; +∞).

d) Tập xác định: D = $ℝ$

Ta có: y' = -3x² + 2x

y' = 0 $\iff$ -3x² + 2x = 0

$\iff$ x.(-3x + 2) = 0

$\iff \left[\begin{array}{l}x=0\\ x=\frac{2}{3}\end{array}\right.$

Bảng biến thiên:

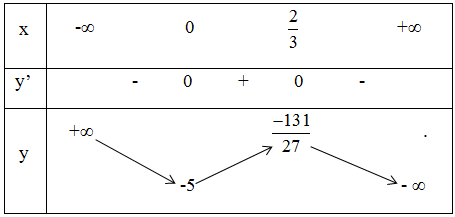
Vậy hàm số nghịch biến trong các khoảng (-∞ ; 0) và $\left(\frac{2}{3};+\infty \right)$, đồng biến trong khoảng $\left(0;\frac{2}{3}\right)$.

Bài 2 trang 10 Toán 12 Giải tích: Tìm các khoảng đơn điệu của các hàm số:

a) $y=\frac{3x+1}{1-x};$

b) $y=\frac{x^2-2x}{1-x};$

c) $y=\sqrt{x^2-x-20}$;

d) $y=\frac{2x}{x^2-9}$ .

Lời giải:

a) Tập xác định: D = $ℝ$ \ {1}

Ta có: 

$$\begin{gathered} y=\frac{3x+1}{1-x} \\ =\frac{-3\left(1-x\right)+4}{1-x} \\ =-3+\frac{4}{1-x} \\ \Rightarrow y^{\text{'}}=\frac{4}{{\left(1-x\right)}^2}>0\forall x\in D \end{gathered}$$

Lại có: y'  không xác định tại x = 1

Ta có:

$$\begin{gathered} \underset{x\to +\infty }{\lim }y=\underset{x\to +\infty }{\lim }\frac{3x+1}{1-x}=\frac{3}{-1}=-3 \\ \underset{x\to -\infty }{\lim }y=\underset{x\to -\infty }{\lim }\frac{3x+1}{1-x}=\frac{3}{-1}=-3 \end{gathered}$$

Do đó ta có bảng biến thiên:

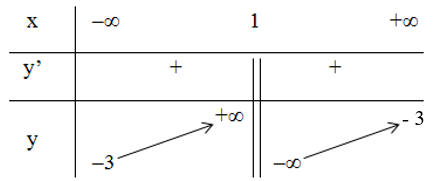
Vậy hàm số đồng biến trên các khoảng (-∞; 1) và (1; +∞).

b) Tập xác định: D = $ℝ$ \ {1}

Ta có:  

$$\begin{gathered} y^{\text{'}}=\frac{\left(2x-2\right)\left(1-x\right)+\left(x^2-2x\right)}{{\left(1-x\right)}^2} \\ =\frac{-x^2+2x-2}{{\left(1-x\right)}^2} \end{gathered}$$

y’ < 0 với mọi x thuộc D

(vì –x² + 2x – 2 = – (x – 1)² – 1 < 0).

y' không xác định tại x = 1

Bảng biến thiên:

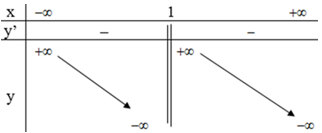
Vậy hàm số nghịch biến trong các khoảng (-∞ ;1) và (1 ; +∞).

c) Tập xác định: D = (-∞ ; -4] $\cup$ [5; +∞)

Ta có:

$y^{\text{'}}=\frac{2x-1}{2\sqrt{x^2-x-20}}$

Có $y^{\text{'}}=0\iff \frac{2x-1}{2\sqrt{x^2-x-20}}=0$

$$\begin{gathered} \iff 2x – 1 = 0 \\ \iff x=\frac{1}{2}\notin D \end{gathered}$$

y' không xác định tại x = -4 và x = 5.

Nên ta có bảng biến thiên:

Vậy hàm số nghịch biến trong khoảng (-∞; -4); đồng biến trong khoảng (5; +∞).

d) Tập xác định: D = $ℝ$ \ {±3}

Ta có:

$$\begin{gathered} y^{\text{'}}=\frac{2\left(x^2-9\right)-2x.2x}{{\left(x^2-9\right)}^2} \\ =\frac{-2\left(x^2+9\right)}{{\left(x^2-9\right)}^2} \end{gathered}$$

Vì $x^2\ge 0\forall x\Rightarrow$ x² + 9 > 0 với mọi x

nên -2(x² + 9) < 0 với mọi x

Mà (x² - 9)² > 0 với mọi x thuộc D

Suy ra: y’ < 0 với mọi x thuộc D.

y' không xác định tại x = ±3

Lại có:

$$\begin{gathered} \underset{x\to \infty }{\lim }y=\underset{x\to \infty }{\lim }\frac{2x}{x^2-9}=0 \\ \underset{x\to -3^{-}}{\lim }y=\underset{x\to -3^{-}}{\lim }\frac{2x}{x^2-9}=-\infty \\ \underset{x\to -3^{+}}{\lim }y=\underset{x\to -3^{+}}{\lim }\frac{2x}{x^2-9}=+\infty \\ \underset{x\to 3^{-}}{\lim }y=\underset{x\to 3^{-}}{\lim }\frac{2x}{x^2-9}=-\infty \\ \underset{x\to 3^{+}}{\lim }y=\underset{x\to 3^{+}}{\lim }\frac{2x}{x^2-9}=+\infty \end{gathered}$$

Nên ta có bảng biến thiên:

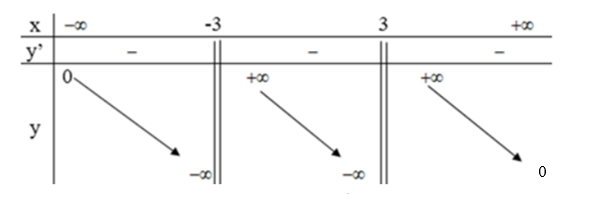
Vậy hàm số nghịch biến trong các khoảng (-∞ ; -3); ( -3; 3) và (3; +∞ ).

Bài 3 trang 10 Toán 12 Giải tích: Chứng minh rằng hàm số $y=\frac{x}{x^2+1}$ đồng biến trên khoảng (-1; 1), nghịch biến trên các khoảng (-∞; -1) và (1; +∞).

Lời giải:

TXĐ: D = $ℝ$

Ta có:

$$\begin{gathered} y^{\text{'}}=\frac{1.\left(x^2+1\right)-2x.x}{{\left(x^2+1\right)}^2} \\ =\frac{1-x^2}{{\left(x^2+1\right)}^2} \end{gathered}$$

Do (x² + 1)² 0 với mọi số thực x nên:

+ Hàm số nghịch biến khi y’ < 0

$\iff$1 – x² < 0 $\iff$x² > 1

$\iff \left[\begin{array}{l}x<-1\\ x>1\end{array}\right.$

$\iff x\in \left(-\infty ;-1\right)\cup \left(1;+\infty \right)$

+ Hàm số đồng biến khi y’ > 0

$\iff$1 – x² > 0 $\iff$x² < 1  

$\iff$– 1 < x < 1

$\iff x\in \left(-1;1\right)$.

Vậy hàm số đồng biến trên khoảng (-1; 1) và nghịch biến trên các khoảng (-∞; -1) và (1; +∞).

Bài 4 trang 10 Toán 12 Giải tích: Chứng minh rằng hàm số $y=\sqrt{2x-x^2}$ đồng biến trên khoảng (0; 1), nghịch biến trên khoảng (1; 2).

Lời giải:

TXĐ: D = [0; 2]

Ta có: $y^{\text{'}}=\frac{2-2x}{2\sqrt{2x-x^2}}=\frac{1-x}{\sqrt{2x-x^2}}$ với mọi x thuộc (0; 2)

Do $\sqrt{2x-x^2}>0\forall x\in \left(0;2\right)$ nên:

+ Hàm số đồng biến khi y’ > 0 với mọi x (0; 2)

$\iff$1 – x > 0$\iff$x < 1

Do đó: 0 < x < 1.

+ Hàm số nghịch biến y’ < 0 với mọi x (0; 2)

$\iff$1 – x < 0 $\iff$x > 1

Do đó: 1 < x < 2.

Vậy hàm số đồng biến trên khoảng (0; 1), nghịch biến trên khoảng (1; 2).

Bài 5 trang 10 Toán 12 Giải tích: Chứng minh các bất đẳng thức sau:

a) tan x > x $\left(0<x<\frac{\pi }{2}\right);$

b) tan x > x + $\frac{x^3}{3}$ $\left(0<x<\frac{\pi }{2}\right).$

Lời giải:

a) Xét hàm số

y = f(x) = tanx – x trên khoảng $\left(0;\frac{\pi }{2}\right)$

Ta có:

$y^{\text{'}}=\frac{1}{co{s}^{2}x}-1={\tan }^{2}x>0$ với mọi số thực x

Suy ra hàm số đồng biến trên khoảng $\left(0;\frac{\pi }{2}\right)$

Do đó: f(x) > f(0) với mọi $x\in \left(0;\frac{\pi }{2}\right)$

Lại có: f(0) = tan 0 – 0 = 0

Khi đó: tan x – x > 0 với mọi $x\in \left(0;\frac{\pi }{2}\right)$

tan x > x với mọi $x\in \left(0;\frac{\pi }{2}\right)$ (đpcm).

b) Xét hàm số

y = g(x) = tanx – x – $\frac{x^3}{3}$ trên $\left(0;\frac{\pi }{2}\right)$

Ta có: 

$$\begin{gathered} g^{\text{'}}\left(x\right)=\frac{1}{co{s}^{2}x}-1-x^2 \\ ={\tan }^{2}x-x^2 \end{gathered}$$

= (tan x – x)(tan x + x)

Theo kết quả câu a) ta có:

tan x – x > 0 với mọi $x\in \left(0;\frac{\pi }{2}\right)$,

hơn nữa tan x + x > 0 với mọi $x\in \left(0;\frac{\pi }{2}\right)$.

Do đó: $g^{\text{'}}\left(x\right)>0\forall x\in \left(0;\frac{\pi }{2}\right)$

Suy ra y = g'(x) đồng biến trên $\left(0;\frac{\pi }{2}\right)$

 $\Rightarrow$ g(x) > g(0) với mọi $x\in \left(0;\frac{\pi }{2}\right)$

Lại có: g(0) = tan 0 – 0 – $\frac{0^3}{3}$ = 0

Do đó: g(x) > 0 với mọi $x\in \left(0;\frac{\pi }{2}\right)$

Hay tanx – x – $\frac{x^3}{3}$ > 0 với mọi $x\in \left(0;\frac{\pi }{2}\right)$

Khi đó: tan > x + $\frac{x^3}{3}$ với mọi $x\in \left(0;\frac{\pi }{2}\right)$(đpcm).

Bài giảng Toán 12 Bài 1: Sự đồng biến, nghịch biến của hàm số

Xem thêm lời giải bài tập Toán lớp 12 hay, chi tiết khác:

Bài 2: Cực trị của hàm số

Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Bài 4: Đường tiệm cận

Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Bài 6: Ôn tập chương 1