Nội dung bài viết

    Xem thêm

    Toán 12 Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

    Với giải bài tập Toán lớp 12 Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 12.

    1 2,082 14/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Mục lục Giải Toán 12 Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

    Hoạt động 1 trang 20 Toán 12 Giải tích: Xét tính đồng biến, nghịch biến và tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:

    a) y = x2 trên đoạn [-3; 0];

    b) y=x+1x−1 trên đoạn [3; 5].

    Lời giải:

    a) Ta có: y' = 2x ≤ 0 trên đoạn [-3; 0]. Vậy hàm số nghịch biến trên đoạn [-3,0].

    Khi đó trên đoạn [-3,0]: hàm số đạt giá trị lớn nhất tại x = -3 và giá trị lớn nhất bằng 9, hàm số đạt giá trị nhỏ nhất tại x = 0 và giá trị nhỏ nhất = 0.

    b) Ta có: y'=x−1−x−1x−12=−2x−12<0 trên đoạn [3; 5]. Vậy hàm số nghịch biến trên đoạn [3; 5].

    Khi đó trên đoạn [3; 5]: hàm số đạt giá trị lớn nhất tại x = 3 và giá trị lớn nhất bằng 2, hàm số đạt giá trị nhỏ nhất tại x = 5 và giá trị nhỏ nhất bằng 32.

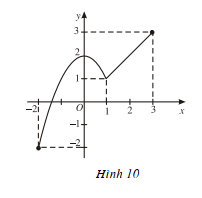
    Hoạt động 2 trang 21 Toán 12 Giải tích: Cho hàm số y=−x2+2  khi  −2≤x≤1x                 khi  1<x≤3có đồ thị như Hình 10. Hãy chỉ ra giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [-2; 3] và nêu cách tính.

    Tài liệu VietJack

    Lời giải:

    Giá trị nhỏ nhất của hàm số trên đoạn [-2; 3] là điểm thấp nhất của đồ thị trên đoạn đó. Vậy quan sát đồ thị ta thấy hàm số đạt giá trị nhỏ nhất tại x = -2. Thay x = -2 vào hàm số y đã cho ta có giá trị nhỏ nhất là -2.

    Giá trị lớn nhất của hàm số trên đoạn [-2; 3] là điểm cao nhất của đồ thị trên đoạn đó. Vậy quan sát đồ thị ta thấy hàm số đạt giá trị lớn nhất tại x = 3. Thay x = 3 vào hàm số y đã cho ta có giá trị lớn nhất là 3.

    Hoạt động 3 trang 23 Toán 12 Giải tích: Lập bảng biến thiên của hàm số fx=−11+x2. Từ đó suy ra giá trị nhỏ nhất của f(x) trên tập xác định.

    Lời giải:

    TXĐ: D = ℝ

    Ta có y'=2x1+x22

    y' = 0 thì 2x1+x22=0⇔x = 0.

    Bảng biến thiên:

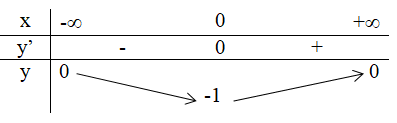
    Lập bảng biến thiên của hàm số f(x) = -1/ 1 + x^2 (ảnh 1)

    Vậy giá trị nhỏ nhất của hàm số đã cho là – 1 tại x = 0.

    Bài 1 trang 23, 24 Toán 12 Giải tích: Tính giá trị lớn nhất và nhỏ nhất của hàm số:

    a) y = x3 – 3x2 – 9x + 35 trên các đoạn [– 4; 4] và [0; 5] ;

    b) y = x4 – 3x2 + 2 trên các đoạn [0; 3] và [2; 5] ;

    c)  y=2−x1−x trên các đoạn [2; 4] và [– 3; – 2] ;

    d)  y=5−4x trên đoạn [– 1; 1].

    Lời giải:

    a) TXĐ: D = ℝ

    Ta có: y' = 3x2 – 6x – 9;

    Có y' = 0 ⇔3x2 – 6x – 9 = 0

    ⇔x = – 1 hoặc x = 3.

    + Xét hàm số trên đoạn [– 4; 4] :

    y(– 4) = – 41 ;

    y(– 1) = 40 ;

    y(3) = 8;

    y(4) = 15.

    Suy ra min−4; 4y=y−4=−41;

    max−4; 4y=y−1=40.

    + Xét hàm số trên [0 ; 5].

    y(0) = 35 ;

    y(3) = 8 ;

    y(5) = 40.

    Suy ra min0; 5y=y3=8;

     max0; 5y=y5=40.

    b) TXĐ: D = ℝ

    Ta có: y' = 4x3 - 6x

    Có y' = 0⇔2x.(2x2 – 3) = 0

    ⇔x=0x=±32

    + Xét hàm số trên [0 ; 3]:

    y(0) = 2;

    y32=−14

    y(3) = 56

    Suy ra min0;3y=y32=−14;

    max0;3y=y3=56.

    + Xét hàm số trên [2; 5].

    y(2) = 6;

    y(5) = 552.

    Suy ra min2;5y=y2=6;

    max2;5y=y5=552.

    c) TXĐ: D = (-∞; 1)  (1; +∞)

    Ta có: y'=11−x2>0   ∀x∈D

    Suy ra hàm số đồng biến trên (-∞; 1) và (1; +∞).

    Do đó hàm số đồng biến trên [2; 4] và [-3; -2].

    Vậy min2;4y=y2=0; max2;4y=y4=23

    min−3;−2y=y−3=54; max−3;−2y=y−2=43.

    d) TXĐ: D=−∞;54

    Ta có:

    y'=−425−4x=−25−4x<0  ∀x∈−∞;−54

    Suy ra hàm số nghịch biến trên −∞;54

    Do đó hàm số nghịch biến trên [-1; 1]

    Vậy min−1;1y=y1=1; max−1;1y=y−1=3.

    Bài 2 trang 24 Toán 12 Giải tích: Trong số các hình chữ nhật có cùng chu vi 16 cm, hãy tìm hình chữ nhật có diện tích lớn nhất.

    Lời giải:

    Nửa chu vi hình chữ nhật là:

    16 : 2 = 8 cm.

    Gọi độ dài 1 cạnh của hình chữ nhật là x (cm) (0 < x < 8)

    Suy ra độ dài cạnh còn lại là :

    8 – x (cm)

    Diện tích của hình chữ nhật là:

    S = x(8 – x) = 8x – x2 

    Xét hàm số

    S(x) = 8x – x2 trên (0; 8)

    Ta có: S' = 8 – 2x; S' = 0

    ⇔8 – 2x = 0 ⇔ x = 4

    S(0) = 0; S(4) = 16; S(8) = 0

    Do đó: Smax = 16 khi x = 4

    Suy ra độ dài cạnh còn lại là

    8 – 4 = 4 (cm)

    Vậy trong các hình chữ nhật có chu vi 16 cm thì hình vuông cạnh bằng 4 cm có diện tích lớn nhất bằng 16cm2.

    Cách khác:

    Ta có: S = x(8 – x) = 8x – x2 

    = 16 – (16 – 8x + x2)

    = 16 – (x – 4)2 ≤ 16.

    Suy ra: Smax = 16

    Dấu bằng xảy ra khi (x – 4)2 = 0⇔x = 4.

    Bài 3 trang 24 Toán 12 Giải tích:

    Bài 4 trang 24 Toán 12 Giải tích:

    Bài 5 trang 24 Toán 12 Giải tích:

    Bài giảng Toán 12 Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

    Xem thêm lời giải bài tập Toán lớp 12 hay, chi tiết khác:

    Bài 4: Đường tiệm cận

    Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số

    Bài 6: Ôn tập chương 1

    Bài 1: Lũy thừa

    Bài 2: Hàm số lũy thừa

    Xem thêm tài liệu Toán lớp 12 hay, chi tiết khác:

    Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

    Trắc nghiệm Giá trị lớn nhất, giá trị nhỏ nhất của hàm số có đáp án

    Tham khảo các loạt bài Toán 12 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 2,082 14/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: