25 câu hỏi trắc nghiệm thuộc 120 câu trắc nghiệm Phương pháp tọa độ trong mặt phẳng nâng cao (P1)

Cách tìm vecto pháp tuyến của đường thẳng (hay, chi tiết)

Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng song song với trục Ox?

A. (0; 1)

B. (1; 0)

C. (-1; 1)

D. (1; 1)

Xem đáp án

Đáp án A

Trục Ox có phương trình đường thẳng là y = 0. Đường thẳng này có VTPT là (0; 1).

Các đường thắng song song với nhau sẽ có cùng VTCP và có cùng VTPT nên các đường thẳng song song với trục Ox có VTPT là (0; 1) .

Câu 5:

05/11/2024

Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng song song với trục Oy?

A. (0; -3)

B. (1; -1)

C. (-3; 0)

D.( 3; 3)

Xem đáp án

Đáp án đúng là C

Lời giải

Trục Oy có phương trình đường thẳng là x = 0. Đường thẳng này có VTPT là ( 1; 0) và có VTCP (0; 1)

Mà các đường thẳng song song với nhau có cùng VTPT và VTCP nên câc đường thẳng song song với trục Oy có VTPT là (1; 0)

Mà 2 vecto ( 1; 0) và ( -3; 0) là 2 vecto cùng phương nên vecto ( -3; 0) cũng là VTPT của trục Oy.

*Phương pháp giải:

Bước 1. Xác định xem phương trình đường thẳng d được cho ở dạng nào: phương trình tổng quát hay phương trình tham số.

Bước 2. Xác định vectơ chỉ phương (VTCP), vectơ pháp tuyến (VTPT), hệ số góc của đường thẳng d:

⦁ Nếu phương trình đường thẳng d có dạng: ax + by + c = 0 thì phương trình đường thẳng d nhận vectơ $\vec{n} = (a; b)$ làm VTPT.

⦁ Nếu phương trình đường thẳng d có dạng: $\{\begin{cases} x = x_{0} + u_{1} t \\ y = y_{0} + u_{2} t \end{cases}$ thì phương trình đường thẳng d nhận vectơ $\vec{u} = (u_{1}; u_{2})$ làm VTCP.

*Lý thuyết:

I. Vecto pháp tuyến của mặt phẳng.

1. Định nghĩa:

Cho mặt phẳng (α). Nếu vecto $\vec{n} \neq \vec{0}$ và có giá vuông góc với mặt phẳng (α) thì $\vec{n}$ được gọi là vecto pháp tuyến của (α)

2. Chú ý. Nếu $\vec{n}$ là vecto pháp tuyến của một mặt phẳng thì $k \vec{n} (k \neq 0)$ cũng là vecto pháp tuyến của mặt phẳng đó.

3. Tích có hướng của hai vectơ

- Định nghĩa: Trong không gian Oxyz, cho hai vectơ $\vec{a} = (a_{1}; a_{2}; a_{3})$ , $\vec{b} = (b_{1}; b_{2}; b_{3})$ . Tích có hướng của hai vectơ $\vec{a}$ và $\vec{b}$ kí hiệu là $[\vec{a}, \vec{b}]$ , được xác định bởi

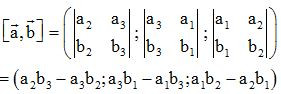
- Chú ý: Tích có hướng của hai vectơ là một vectơ, tích vô hướng của hai vectơ là một số.

Xem thêm

120 câu trắc nghiệm Phương pháp tọa độ trong mặt phẳng nâng cao

Câu 6:

Vectơ nào dưới đây là một vectơ pháp tuyến của đường phân giác góc phần tư thứ hai?

A. (1; 0)

B. (1; -2)

C. (2; -2)

D.( 4;4)

Xem đáp án

Đáp án C

Phương trình đường phân giác góc phần tư thứ hai là (d) : x+ y= 0.

Đường thẳng này có VTPT là (1; 1) nên có VTCP là (1;- 1)

Mà vecto (1; 1) và (4; 4) là 2 vecto cùng phương nên vecto (4;4) cũng là VTPT của đường thẳng (d)

Câu 7:

Đường thẳng d có một vectơ chỉ phương là $\vec{u} (- 2; - 3) .$ Đường thẳng vuông góc với d có một vectơ pháp tuyến là:

A.(2;-3)

B. (4;6)

C. (6; 4)

D.(3; -2)

Xem đáp án

Đáp án B

Ta có nhận xét:

Hai đường thẳng vuông góc với nhau thì VTPT của đường thẳng này là VTCP của đường thẳng kia và ngược lại.

Do đường thẳng ∆ vuông góc với đường thẳng (d) nên nhận VTCP của đường thẳng (d) là VTPT. Do đó: 1 VTPT của đường thẳng ∆ là ( -2; -3).

Mà hai vectơ (-2; -3) và ( 4; 6) là 2 vectơ cùng phương nên vectơ (4; 6) cũng là VTPT của đường thẳng ∆.

Câu 8:

Đường thẳng (d) có một vectơ pháp tuyến là $\vec{n} (2; - 1) .$ Đường thẳng ∆ vuông góc với d có một vectơ chỉ phương là:

A. (2; -1)

B. (-1; 2)

C. (2; 1)

D.(1; 2)

Xem đáp án

Đáp án A

Do hai đường thẳng vuông góc với nhau thì VTPT của đường thẳng này là VTCP của đường thẳng kia và ngược lại.

Do đường thẳng ∆ vuông góc với đường thẳng (d) nên nhận VTPT của đường thẳng ( d) là VTCP. Do đó: một VTCP của đường thẳng ∆ là ( 2; -1)

Câu 9:

Tìm vectơ pháp tuyến của đường thẳng đi qua hai điểm A(1; 4) và B( 3; 6).

A. (4; 10)

B.(10; -4)

C.(2; -2)

D. (2; 2)

Xem đáp án

Đáp án C

Đường thẳng AB nhận $\vec{A B} (2; 2)$ là VTCP . Do đó VTPT của đường thẳng AB là ( 2; -2)

Câu 10:

17/07/2024

Đường thẳng (d) có phương trình là 2x+ 3y- 6= 0. Đường thẳng vuông góc với (d) có một vectơ pháp tuyến là:

A. (3; 2)

B. (2; -3)

C. (2; 3)

D.(3; -2)

Xem đáp án

Chọn D

Đường thẳng (d) có VTPT là (2;3) và VTCP là (3; -2)

Do đường thẳng (d) và ∆ vuông góc với nhau nên đường thẳng ∆ nhận VTCP của đường thẳng (d) làm VTPT.

Do đó đường thẳng ∆ có VTPT là (3; -2) .

Câu 11:

23/07/2024

Đường thẳng d có một vectơ chỉ phương là $\vec{u} = (3; - 4) .$ Đường thẳng ∆ song song với d có một vectơ pháp tuyến là:

Xem đáp án

Đáp án A

Đường thẳng ( d) có VTCP là $\vec{u} = (3; - 4)$

Nên đường thẳng (d) có 1 VTPT là ( 4; 3) .

Do 2 đườg thẳng ∆ và (d) song song với nhau nên chúng có cùng VTPT và cùng VTCP .

Suy ra đường thẳng ∆ có 1 VTPT là (4; 3) .

Câu 12:

23/07/2024

Đường thẳng d có một vectơ pháp tuyến là $\vec{n} = (- 2; - 5)$ Đường thẳng ∆ song song với d có một vectơ chỉ phương là:

Xem đáp án

Đáp án A

Đường thẳng d có một vectơ pháp tuyến là $\vec{n} = (- 2; - 5)$ nên đường thẳng này có 1 VTCP là: $\vec{n} = (5; - 2)$

Do đường thẳng d và ∆ song song với nhau nên vecto $\vec{n} = (5; - 2)$ cũng là VTCP của đường thẳng ∆.

Câu 13:

Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng song song với trục Ox?

Xem đáp án

Đáp án A

Trục Ox có phương trình tổng quát là: y= 0.

Đường thẳng này có VTPT là ( 0; 1) và VTCP là (1; 0)

Các đường thẳng song song với trục Ox sẽ có cùng VTPT và có cùng VTCP với trục Ox. Nên đường thẳng song song với trục Ox có VTCP là (1; 0) .

Câu 14:

13/07/2024

Cho đường thẳng (d) x-2y+ 8= 0. Đường thẳng ∆ đi qua A(2; -3) và song song với (d) có phương trình:

A. x- 2y+ 6= 0

B. 2x+ y -1= 0

C.x+ 2y-6= 0

D.x-2y-8=0

Xem đáp án

Đáp án D

Do ∆ song song vớo ( d) nên có phương trình dạng: x- 2y+ c= 0

Mà ∆ đi qua A( 2; -3) nên ta có

2- 2. (-3) + c= 0

Do đó: c= - 8.

Vậy đường thẳng cần tìm là x- 2y – 8 = 0

Câu 15:

13/07/2024

Cho tam giác ABC có A( 1;2) ; B( 0; 4) và C( 3; -1). Đường thẳng đi qua B và song song với AC có phương trình:

A.3x+ 2y+ 4= 0

B.3x-2y+ 7=0

C. 3x+ 2y- 8 =0

D.2x-3y+ 6=0

Xem đáp án

Đáp án C

Gọi (d) là đường thẳng cần tìm. Do d song song với AC nên d nhận $\vec{A C} (2; - 3)$ làm VTCP.

Suy ra $\vec{n} (3; 2)$ là VTPT của (d) .

Do đó; đường thẳng ( d) có phương trình:

3( x- 0) +2( y-4) = 0 hay 3x+ 2y- 8=0

Câu 16:

15/07/2024

Phương trình tham số của đường thẳng (d) đi qua điểm M( 2; -5) và vuông góc với đường thẳng (d’) : x+ 6y -7= 0 là:

D.Tất cả sai

Xem đáp án

Đáp án A

Do 2 đường thẳng d và (d’) vuông góc với nhau nên VTCP của đường thẳng này là VTPT của đường thẳng kia và ngược lại.

Mà đường thẳng (d’) có VTPT là $\vec{n} (1; 6) n ê n \vec{u} (1; 6)$ là VTCP của đường thẳng (d) .

Khi đó phương trình tham số của đường thẳng (d) cần tìm là:

Câu 17:

Cho tam giác ABC có A( 2; -1) ; B( 4; 5) và C(-3;2) . Phương trình tổng quát của đường cao AH của tam giác ABC là:

A. 3x- 7y+ 11=0

B. 7x+ 3y-11=0

C. 3x-7y-13=0

D.7x+ 3y+13=0

Xem đáp án

Đáp án B

AH là đường cao của tam giác nên đường thẳng này đi qua A( 2; -1) và nhận $\vec{C B} (7; 3)$ làm VTPT .

Suy ra; phương trình đường cao AH là:

7(x- 2) +3( y+1) = 0 hay 7x+ 3y -11= 0

Câu 18:

Viết phương trình tổng quát của đường thẳng d biết d đi qua điểm B( 2; -5) và có hệ số góc k= 2.

A.2x+ y-6=0

B. 2x-y – 6= 0

C. 2x- y- 9= 0

D. Tất cả sai

Xem đáp án

Đáp án C

Phương trình đường thẳng d là.

y = 2( x-2) – 5

Hay 2x-y -9 =0

Câu 19:

Viết phương trình đường thẳng d biết d đi qua điểm N( 1; 4) và có hệ số góc là số nguyên dương nhỏ nhất.

A. x+ y-1= 0

B. x-y+3= 0

C. x+y- 2= 0

D. x+ y- 4= 0

Xem đáp án

Đáp án B

Số nguyên dương nhỏ nhất là 1 nên hệ số góc của đường thẳng (d) là k= 1

Phương trình đường thẳng (d) là

y= 1(x - 1) +4

hay x- y + 3= 0.

Câu 20:

Cho tam giác ABC có phương trình các cạnh AB. x+y-1= 0; AC: 7x- y+2=0 và BC: 10x+ y-19=0. Viết phương trình đường phân giác trong góc A của tam giác ABC.

A. 12x+ 4y-3= 0

B. 2x-6y+7= 0

C. 12x+ 6y+ 5= 0

D. 2x+6y-7=0

Xem đáp án

Đáp án B

Do AB và BC cắt nhau tại B nên toa độ điểm B là nghiệm hệ phương trình

Do đó: B( 2; -1)

Tương tự: tọa độ điểm C( 1; 9)

PT các đường phân giác góc A là:

Đặt T₁(x; y) = 2x- 6y+ 7 và T₂= 12x+ 4y-3 ta có:

T₁(B). T₁(C) < 0 và T₂(B) T₂(C) >0.

Suy ra B và C nằm khác phía so với đường thẳng 2x-6y+7= 0 và cùng phía so với đường thẳng: 12x+ 4y- 3= 0.

Vậy phương trình đường phân giác trong góc A là: 2x- 6y+ 7= 0.

Câu 21:

Cho tam giác ABC có A( -2; -1) ; B( -1; 3) và C(6; 1) . Viết phương trình đường phân giác ngoài góc A của tam giác ABC.

A. x-y+1= 0

B. 5x+ 3y=9=0

C. 3x+ 3y-5= 0

D.x+ y+ 3= 0

Xem đáp án

Đáp án D

Phương trình đường thẳng AB:

$\frac{x + 2}{- 1 + 2} = \frac{y + 1}{3 + 1} h a y 4 x - y + 7 = 0$

Phương trình đường thẳng AC:

$\frac{x + 2}{6 + 2} = \frac{y + 1}{1 + 1} h a y x - 4 y - 2 = 0$

Phương trình các đường phân giác góc A là:

Đặt T₁(x; y) = x+ y+ 3 và T₂= x- y+ 1 ta có:

T₁(B). T₁(C)> 0 và T₂(B) T₂(C) < 0.

Suy ra B và C nằm khác phía so với đường thẳng x-y+ 1= 0 và cùng phía so với đường thẳng: x+ y+ 3= 0.

Vậy phương trình đường phân giác ngoài góc A là: x+ y+ 3= 0.

Câu 22:

Viết phương trình đường thẳng d qua M( -1; 2) và tạo với trục Ox một góc $60^{\circ}$ .

Xem đáp án

Đáp án D

Do đường thẳng d tạo với trục Ox một góc 60⁰ nên có hệ số góc: $k = \tan 60^{\circ} = \sqrt{3}$

Phương trình (d) là: $y = \sqrt{3} x + b$

Vì M ( -1; 2) thuộc vào đường thẳng d nên ta có: $2 = \sqrt{3} . (- 1) + b \Leftrightarrow b = \sqrt{3} + 2$

Khi đó phương trình (d) là: $y = \sqrt{3} x + \sqrt{3} + 2$

hay $\sqrt{3} x - y + \sqrt{3} + 2 = 0$

Câu 23:

Viết phương trình đường thẳng (d) qua N( 3; -2) và tạo với trục Ox một góc 45⁰.

A.x+y-1= 0

B.x- y-5= 0

C. x+ y -1= 0

D. Đáp án khác

Xem đáp án

Đáp án B

Do d tạo với trục Ox một góc 45⁰ nên có hệ số góc k = tan45⁰= 1.

Phương trình d là: y = 1( x-3) -2 hay x- y-5= 0

Câu 24:

20/07/2024

Cho đường thẳng (d) có phương trình: x- 2y+ 5= 0. Có mấy phương trình đường thẳng qua M(2; 1) và tạo với d một góc 45⁰.

A. 1

B. 2

C. 3

D. Không có.

Xem đáp án

Đáp án B

Gọi ∆ là đường thẳng cần tìm và $\vec{n} (A; B)$ là VTPT của ∆ $A^{2} + B^{2} \neq 0$

Để ∆ tạo với đường thẳng ( d) một góc 45⁰ thì:

Tương đương: 2( A- 2B) ²= 5( A²+ B²)

Nên A= -3B hoặc B= 3A

+ Với A= - 3B, chọn B= -1 thì A= 3 ta được phương trình ∆ : 3x- y- 5= 0.

+ Với B= 3A, chọn A= 1 thì B= 3 ta được phương trình ∆: x+ 3y- 5 = 0 .

Câu 25: