Trắc nghiệm Phương trình đường tròn có đáp án (Vận dụng)
-
364 lượt thi
-
15 câu hỏi
-
20 phút
Danh sách câu hỏi
Câu 3:
12/07/2024Phương trình đường tròn (C) đi qua hai điểm A (0; 1), B (1; 0) và có tâm nằm trên đường thẳng: x + y + 2 = 0 là
Xem đáp án
Giả sử điểm I (xI; yI) là tâm của đường tròn (C). Vì I nằm trên đường thẳng x + y + 2 = 0 nên ta có xI + yI + 2 = 0 (1)
Vì đường tròn (C) đi qua hai điểm A (0; 1), B (1; 0) nên ta có IA = IB. Điều này tương đương với
IA2 = IB2 hay
Từ (1) và (2) suy ra . Suy ra I (−1; −1).
Mặt khác ta có R = IA =
Vậy (C) có dạng
Đáp án cần chọn là: D
Câu 4:
21/07/2024Cho tam giác ABC có A (−2; 4), B (5; 5), C (6; −2). Đường tròn ngoại tiếp tam giác ABC có phương trình là
Xem đáp án
Gọi phương trình đường tròn x2 + y2 + 2ax + 2by + c = 0. Khi đó,
Câu 5:
21/07/2024Trong mặt phẳng với hệ trục tọa độ Oxy, cho hai đường thẳng d1: x + y + 5 = 0, d2: x + 2y – 7 = 0 và tam giác ABC có A (2; 3), trọng tâm là G (2; 0), điểm B thuộc d1 và điểm C thuộc d2. Viết phương trình đường tròn ngoại tiếp tam giác ABC
Xem đáp án
Điểm B thuộc d1: x + y + 5 = 0 nên ta giả sử B (b; −b − 5)
Điểm C thuộc d2: x + 2y −7 = 0 nên ta giả sử C (7 − 2c, c)
Vì tam giác ABC có A (2; 3), trọng tâm là G (2; 0) nên ta có hệ phương trình
- Giả sử phương trình đường tròn cần lập có dạng x2 + y2 + 2ax + 2by + c = 0. Vì đường tròn qua 3 điểm A (2; 3), B (−1; −4) và C (5; 1) nên ta có hệ phương trình:
Câu 7:
16/07/2024Trong mặt phẳng Oxy cho đường thẳng (d): 3x − 4y + 5 = 0 và đường tròn (C): . Tìm những điểm M thuộc (C) và N thuộc (d) sao cho MN có độ dài nhỏ nhất
Xem đáp án
Đường tròn (C) có tâm I (−1; 3) và bán kính
MN min ⇔ IN đạt min ⇔ N là chân hình chiếu vuông góc của I xuống đường thẳng d.
Giả sử N (a; b). Vì N ∈ d nên ta có 3a − 4b + 5 = 0 (1)
Mặt khác, ta có: IN vuông góc với d nên
Mà = (a + 1; b − 3), = (4; 3). Suy ra ta có:
4 (a + 1) + 3(b − 3) = 0 ⇔ 4a + 3b – 5 = 0 (2)
Từ (1) và (2) ta có hệ phương trình
Vì d (I; d) = 2R nên M là trung điểm của IN. Do đó, tọa độ của M là:
Đáp án cần chọn là: B
Câu 9:
15/11/2024Tìm tọa độ tâm I của đường tròn đi qua ba điểm A (0; 4), B (2; 4), C (4; 0)
Xem đáp án
Đáp án đúng là D
Lời giải
*Phương pháp giải:
- Gọi phương trình đường tròn là .
- Thay tọa độ các điểm vào phương trình tìm và suy ra tọa độ tâm.
*Lý thuyết:
Trong mặt phẳng Oxy, cho đường tròn (C) tâm I(a; b), bán kính R.
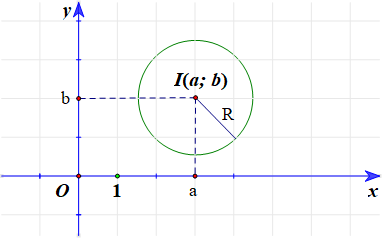Phương trình (x – a)2 + (y – b)2 = R2 được gọi là phương trình đường tròn tâm I(a; b), bán kính R.
Nhận xét: Ta có (x – a)2 + (y – b)2 = R2
⇔ x2 + y2 – 2ax – 2by + (a2 + b2 – R2) = 0.
Vậy phương trình đường tròn (x – a)2 + (y – b)2 = R2 có thể được viết dưới dạng x2 + y2 – 2ax – 2by + c = 0, trong đó c = a2 + b2 – R2.
Ngược lại, phương trình x2 + y2 – 2ax – 2by + c = 0 là phương trình của đường tròn (C) khi và chỉ khi a2 + b2 – c > 0. Khi đó đường tròn (C) có tâm I(a; b) và bán kính .
Xem thêm
Lý thuyết Đường tròn trong mặt phẳng tọa độ – Toán 10 Chân trời sáng tạo
Câu 10:
22/07/2024Đường tròn (x − a)2 + (y − b)2 = R2 cắt đường thẳng x + y – a – b = 0 theo một dây cung có độ dài bằng bao nhiêu ?
Xem đáp án
x + y – a – b = 0 ⇔ y = a + b – x thay vào (x − a)2 + (y − b)2 = R2 ta có
(x − a)2 + (x − a)2 = R2
Câu 11:
21/07/2024Đường thẳng d: 4x + 3y + m = 0 tiếp xúc với đường tròn (C): x2 + y2 = 1 khi
Xem đáp án
(C): x2 + y2 = 1 có tâm O (0; 0) và bán kính R = 1
Do đó, d tiếp xúc với đường tròn (C) khi d(I; d) = R hay ta có phương trình
⇔ m = ±5
Đáp án cần chọn là: B
Câu 12:
23/07/2024Cho (C): , một phương trình tiếp tuyến của (C) vuông góc với đường thẳng (d): 3x + 4y – 37 = 0 là:
Xem đáp án
(C): có tâm I(−2; 1) ;R=
Tiếp tuyến vuông góc với đường thẳng (d): 3x + 4y – 37 = 0 nên phương trình tiếp tuyến có dạng 4x − 3y + c = 0 (d’)
Vì d’ là tiếp tuyến của đường tròn có tâm I(−2; 1) và R = 5 nên ta có
d(I; d′) = R ⇔ ⇔ |c − 11| = 25 ⇔ c = 36 hoặc c = −14
Đáp án cần chọn là: C
Câu 13:
23/07/2024Cho đường tròn (C): và đường thẳng (d): x – y – 1 = 0. Một tiếp tuyến của (C) song song với d có phương trình là:
Xem đáp án
(C): có tâm I(2; 2), R = = 4
Tiếp tuyến song song với đường thẳng (d): x – y – 1 = 0 nên phương trình tiếp tuyến có dạng x – y + c = 0 với c ≠ −1 (d’)
Vì d’ là tiếp tuyến của đường tròn có tâm I(2; 2) và R = 4 nên ta có
d(I; d′) = R
Đáp án cần chọn là: C
Câu 14:
23/07/2024Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): . Số phương trình tiếp tuyến của (C), biết góc giữa tiếp tuyến này và trục hoành bằng 600
Xem đáp án
Tiếp tuyến tạo với trục hoành một góc 600 ⇔ hệ số góc của tiếp tuyến là tan600 hoặc tan1200
Do đó tiếp tuyến d có dạng hoặc
Đường tròn (C): có tâm I(−1; 0) và bán kính R = 1
d tiếp xúc với đường tròn ⇔ d(I, d) = R
Câu 15:
21/07/2024Trong mặt phẳng với hệ tọa độ Oxy. Cho đường tròn (C): và đường thẳng d: x + y + 1 = 0. Tìm những điểm M thuộc đường thẳng d sao cho từ điểm M kẻ được đến (C) hai tiếp tuyến hợp với nhau góc 900
Xem đáp án
- M thuộc d suy ra M (t; −1 − t).
Nếu 2 tiếp tuyến vuông góc với nhau thì MAIB là hình vuông (A, B là 2 tiếp điểm). Do đó
