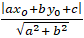Trắc nghiệm Phương trình đường tròn có đáp án (Tổng hợp)
-
281 lượt thi
-
29 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 8:
12/07/2024Cho tam giác ABC có A (1; −2), B (−3; 0), C (2; −2). Tam giác ABC nội tiếp đường tròn có phương trình là
Xem đáp án
Gọi phương trình đường tròn x2 + y2 + 2ax + 2by + c = 0. Khi đó
Câu 10:
22/07/2024Với những giá trị nào của m thì đường thẳng Δ: 4x + 3y + m = 0 tiếp xúc với đường tròn (C): x2 + y2 – 9 = 0
Xem đáp án
Do đường tròn tiếp xúc với đường thẳng Δ nên
R = d(I, Δ) = 
⇔ m = ±15
Đáp án cần chọn là: D
Câu 11:
05/11/2024Với những giá trị nào của m thì đường thẳng D: 3x + 4y + 3 = 0 tiếp xúc với đường tròn (C): (x − m)2 + y2 = 9
Xem đáp án
Lời giải
Đường tròn có tâm I (m; 0) và bán kính R = 3.
Đường thẳng tiếp xúc với đường tròn khi và chỉ khi d(I; Δ) = R = 3
Đáp án đúng là: B
*Phương pháp giải:
+ Cho đường tròn ( C) tâm I( a;b) bán kính R và đường thẳng d.
Đường thẳng d tiếp xúc với đường tròn ( C) khi và chỉ khi : d(I, d)= R
+ Trục tung có phương trình x= 0 nên để đường tròn tiếp xúc với trục tung khi và chỉ khi:
= R hay R = |a|
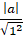
+ Trục hoành có phương trình y= 0 để đường tròn tiếp xúc với trục hoành khi và chỉ khi:
= R hay R = |b|.
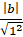
+ Đường tròn tiếp xúc với hai trục tọa độ khi và chỉ khi:
R = |a| = |b|.
Chú ý: Cho đường thẳng d: ax + by + c= 0 và điểm M(x0; y0) . Khoảng cách từ điểm M đến đường thẳng d là: d(M; d) = 
*Lý thuyết:
Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính tại điểm đó thì đường thẳng đó là tiếp tuyến của đường tròn.
- Nếu khoảng cách từ tâm của một đường tròn đến đường thẳng bằng bán kính của đường tròn thì đường thẳng đó là tiếp tuyến của đường tròn.
- Từ một điểm trên đường tròn ta có duy nhất một tiếp tuyến đi qua điểm đó. Từ một điểm ngoài đường tròn, ta có hai tiếp tuyến với đường tròn đi qua điểm đó.
Xem thêm
Phương trình tiếp tuyến của đường tròn (lý thuyết, công thức và cách giải các dạng bài tập)
TOP 40 câu Trắc nghiệm Dấu hiệu nhận biết tiếp tuyến của đường tròn (có đáp án 2024) – Toán 9
Câu 12:
13/07/2024Cho đường tròn (C): x2 + y2 − 2x + 4y – 4 = 0. Đường thẳng nào sau đây là tiếp tuyến của đường tròn:
Xem đáp án
(C): x2 + y2 − 2x + 4y – 4 = 0 có tâm I (1; −2) và bán kính
Nếu d có phương trình x = 1 ta có d(I; d) = |1 − 1| = 0 ≠ R. Loại A
Nếu d có phương trình x + y – 2 = 0 thì ta có
d(I;d) = . Loại B
Nếu d có phương trình 2x + y – 1 = 0 thì ta có
d(I;d)=≠ R. Loại C
Nếu d có phương trình y = 1 ta có d(I; R) = |1 − (−2)| = 3 = R
Vậy d là tiếp tuyến của (C)
Đáp án cần chọn là: D
Câu 13:
22/07/2024Trục Oy là tiếp tuyến của đường tròn nào sau đây?
Xem đáp án
Do đường tròn tiếp xúc với trục Oy nên R = d(I, Oy) = |xI|.
Phương trình trục Oy là x = 0.
Đáp án A sai vì: Tâm I (0; 5) và bán kính . Ta có:
d (I, Oy) = |xI| ≠ R.
Đáp án B sai vì: Tâm và bán kính . Ta có:
d (I, Oy) = |xI| ≠ R.
Đáp án C đúng vì: Tâm I (1; 0) và bán kính R = 1. Ta có:
d (I, Oy) = |xI| = R.
Đáp án D sai vì: Tâm I (0; 0) và bán kính R =. Ta có:
d (I, Oy) = |xI| ≠ R
Đáp án cần chọn là: C
Câu 14:
22/07/2024Đường tròn nào sau đây tiếp xúc với trục Ox?
Xem đáp án
Do đường tròn tiếp xúc với trục Ox nên R = d(I,Ox) = |yI|.
Phương trình trục Ox là y = 0.
Đáp án A sai vì: Tâm I(1; 5) và bán kính R=. Ta có
d(I, Ox) = |yI| ≠ R.
Đáp án B đúng vì: Tâm và bán kính . Ta có
d(I, Ox) = |yI| = R.
Đáp án C sai vì: Tâm I(0; 5) và bán kính R=. Ta có
d(I, Ox) = |yI| ≠ R.
Đáp án D sai vì: Tâm I(0; 0) và bán kính R=. Ta có
d(I, Ox) = |yI| ≠ R.
Đáp án cần chọn là: B
Câu 15:
23/07/2024Đường tròn x2 + y2 − 4x − 2y + 1 = 0 tiếp xúc đường thẳng nào trong các đường thẳng dưới đây?
Xem đáp án
Ta có: x2 + y2 − 4x − 2y + 1 = 0 ⇔ (x − 2)2 + (y − 1)2 = 4 có tâm I(2; 1), bán kính R = 2.
Vì d(I, Oy) = 2, d(I, Ox) = 1,d(I, Δ1) = , d(I, Δ2) = nên A đúng.
Đáp án cần chọn là: A
Câu 16:
12/07/2024Tiếp tuyến với đường tròn (C): x2 + y2 = 2 tại điểm M(1; 1) có phương trình là
Xem đáp án
(C) có tâm O (0; 0) bán kính R =. Ta thấy M ∈ (C). Có = (1; 1) là 1 vecto pháp tuyến của tiếp tuyến tại M. Do đó phương trình tiếp tuyến tại M là :
1(x − 1) + 1.(y − 1) = 0 ⇔ x + y – 2 = 0
Đáp án cần chọn là: A
Câu 17:
21/07/2024Đường tròn (C) có tâm I thuộc đường thẳng d: x + 3y + 8 = 0, đi qua điểm A (−2; 1) và tiếp xúc với đường thẳng Δ: 3x − 4y + 10 = 0. Phương trình của đường tròn (C) là
Xem đáp án
Dễ thấy A ∈ Δ nên tâm I của đường tròn nằm trên đường thẳng qua A vuông góc với Δ là
Câu 18:
22/07/2024Xác định vị trí tương đối giữa 2 đường tròn và
Xem đáp án
Vậy hai đường tròn có tất cả 2 điểm chung nên chúng cắt nhau.
Đáp án cần chọn là: C
Câu 20:
19/07/2024Cho đường tròn và điểm M (4; 1). Viết phương trình tiếp tuyến của đường tròn và đi qua M
Xem đáp án
Đường tròn (C) có tâm I (1; 3) và bán kính R = 2.
Gọi d là tiếp tuyến cần tìm.
Ta có d đi qua điểm M (4; 1) nên phương trình d có 2 dạng.
+) d1: x = 4. Khi đó d(I; d) = |4 − 1| = 3 > R nên d1: x = 4 không phải là tiếp tuyến.
+) d2: y = k(x − 4) + 1 ⇔ kx – y + 1 – 4k = 0
Vì d2 là tiếp tuyến nên ta có
Vậy có 2 tiếp tuyến thỏa yêu cầu đề bài y = 1 và 12x + 5y – 53 = 0
Đáp án cần chọn là: A
Câu 21:
21/07/2024Trong mặt phẳng Oxy, cho hai đường tròn (C1): và (C2): cắt nhau tại A (2; 3).Viết phương trình tất cả đường thẳng d đi qua A và cắt (C1), (C2) theo hai dây cung có độ dài bằng nhau
Xem đáp án
- Từ giả thiết: (C1): I = (0; 0), R =. (C2) ; J (6; 0), R′ = 5
- Gọi đường thẳng d qua A (2; 3) có véc tơ chỉ phương
= (a; b) ⇒ d: a(x − 2) + b(y − 3) = 0 ⇔ ax + by − 2a − 3b = 0
Dễ thấy AH = AK (vì AM = AN) nên IA2 – IH2 = JA2 – JK2
⇔ 13 – d2(I, d) = 25 – d2(J, d)
⇔ d2(J, d) – d2(I, d) = 12
Nếu b = 0 thì chọn a = 1 ta được phương trình x – 2 = 0.
Nếu b = −3a thì chọn a = 1 ta được b = −3, ta được phương trình x − 3y + 7 = 0.
Vậy có 2 đường thẳng: d1: x – 2 = 0 và d2: x − 3y + 7 = 0.
Đáp án cần chọn là: A
Câu 22:
19/07/2024Trong mặt phẳng với hệ toạ độ Oxy, cho đường tròn (C) có phương trình: . Tia Oy cắt (C) tại A (0; 2). Lập phương trình đường tròn (C′), bán kính R′ = 2 và tiếp xúc ngoài với (C) tại A
Xem đáp án
- (C) có , R = 4. Gọi J là tâm đường tròn cần tìm: J (a; b)
⇒ (C′): (x − a)2 + (y − b)2 = 4
-Do (C) và (C′) tiếp xúc ngoài với nhau cho nên khoảng cách IJ = R + R′
Câu 23:
21/07/2024Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C) có phương trình . Tìm điểm M thuộc trục tung sao cho qua M kẻ được hai tiếp tuyến với (C) mà góc giữa hai tiếp tuyến đó bằng 600
Xem đáp án
Viết lại phương trình của (C) dưới dạng: (x − 3)2 + y2 = 4.
Từ đó, (C) có tâm I (3; 0) và bán kính R = 2
Giao của đường tròn với trục tung (x = 0) là: (−3)2 + y2 = 4.
Nên y2 = −5 (vô lý)
Suy ra trục tung không có điểm chung với đường tròn (C).
Gọi M(0; m) ∈ Oy mà góc giữa hai tiếp tuyến ME, MF bằng 600
Khi đó suy ra
Câu 24:
22/07/2024Trong mặt phẳng (Oxy), cho đường tròn (C): và hai điểm A (−2; 0), B (4; 3). Viết phương trình các tiếp tuyến của (C) tại các giao điểm của (C) với đường thẳng AB
Xem đáp án
⇒ (C) có tâm và bán kính
Đường thẳng AB với A (−2; 0) và B (4; 3) có phương trình
+ Giao điểm của (C) với đường thẳng AB có tọa độ là nghiệm hệ PT
Vậy có hai giao điểm là M (0; 1) và N (2; 2)
+ Các tiếp tuyến của (C) tại M và N lần lượt nhận các vectơ và làm các vectơ pháp tuyến, do đó các TT đó có phương trình lần lượt là:
Câu 25:
13/07/2024Cho đường tròn (C): và điểm K (4; 1). Gọi điểm M (a; b) thuộc trục Oy sao cho từ M kẻ được hai tiếp tuyến với (C) tại các tiếp điểm A, B mà AB đi qua K. Khi đó giá trị của biểu thức T = a2 + b2 là
Xem đáp án
Đường tròn (C): có tâm I (4; 0) và bán kính R = 2.
Gọi (C′) là đường tròn tâm M bán kính MA thì A, B là các giao điểm của hai đường tròn (C) và (C′).
Điểm M ∈ Oy ⇒ M (0; m). Khi đó
Đường tròn (C′) tâm M (0; m) bán kính có phương trình:
Lấy (1) − (2) ta được:
−8x + 2my + 24 = 0 hay phương trình AB: −8x + 2my + 24 = 0.
Do K (4; 1) ∈ AB nên −8.4 + 2m.1 + 24 = 0 ⇔ m = 4.
Vậy M (0; 4) hay a = 0, b = 4 ⇒ T = 02 + 42 = 16
Đáp án cần chọn là: C
Câu 26:
20/07/2024Trong mặt phẳng với hệ tọa độ Oxy, cho điểm A(−1; 1) và B(3; 3), đường thẳng Δ: 3x − 4y + 8 = 0. Có mấy phương trình đường tròn qua A, B và tiếp xúc với đường thẳng Δ?
Xem đáp án
Tâm I của đường tròn nằm trên đường trung trực d của đoạn AB.
Gọi d là đường trung trực của AB thì d đi qua trung điểm M(1; 2) của AB và có VTPT là = (4; 2)
Câu 27:
23/07/2024Trong mặt phẳng với hệ tọa độ Oxy cho hai đường thẳng Δ: x + 3y + 8 =0 , Δ′: 3x − 4y + 10 = 0 và điểm A (−2; 1). Viết phương trình đường tròn có tâm thuộc đường thẳng , đi qua điểm A và tiếp xúc với đường thẳng Δ′
Xem đáp án
Tâm I của đường tròn thuộc Δ nên I (−3t – 8; t)
Theo yc thì k/c từ I đến Δ′ bằng k/c IA nên ta có
Khi đó I (1; −3), R = 5 và pt cần tìm:
Đáp án cần chọn là: D
Câu 28:
12/07/2024Trong mặt phẳng Oxy cho và đường thẳng d: 3x − 4y + m = 0 . Tìm m để trên d có duy nhất điểm P sao cho từ P vẽ 2 tiếp tuyến PA, PB của đường tròn và tam giác PAB là tam giác đều
Xem đáp án
(C) có tâm I (1; −2) và bán kính R = 3
Ta có: ΔPAB đều
Suy ra P thuộc đường tròn (C′) tâm I, bán kính R′ = 6.
Trên d có duy nhất một điểm P thỏa mãn yêu cầu bài toán khi và chỉ khi d tiếp xúc với (C′) tại P
Câu 29:
23/07/2024Trong mặt phẳng với hệ toạ độ Oxy, cho đường tròn (C): . Viết phương trình đường thẳng song song với đường thẳng d: 3x + 4y – 2 = 0 và cắt đường tròn theo một dây cung có độ dài bằng 6.
Xem đáp án
Gọi Δ là đường thẳng song song với d nên Δ có dạng 3x + 4y + c = 0 (c ≠ −2)
Δ cắt (C) tại A, B nên AB = 6.
Gọi H là trung điểm của AB thì
