Lý thuyết Hàm số và đồ thị – Toán 10 Chân trời sáng tạo
Với lý thuyết Toán lớp 10 Bài 1: Hàm số và đồ thị chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sách Chân trời sáng tạo sẽ giúp học sinh nắm vững kiến thức trọng tâm để học tốt môn Toán 10.
Lý thuyết Toán 10 Bài 1: Hàm số và đồ thị - Chân trời sáng tạo
A. Lý thuyết
1. Hàm số. Tập xác định và tập giá trị của hàm số
- Giả sử x và y là hai đại lượng biến thiên và x nhận giá trị thuộc tập số D.
Nếu với mỗi giá trị x thuộc D, ta xác định được một và chỉ một giá trị tương ứng y thuộc tập hợp số thực ℝ thì ta có một hàm số.
Ta gọi x là biến số và y là hàm số của x.
Tập hợp D được gọi là tập xác định của hàm số.
Tập hợp T gồm tất cả các giá trị y (tương ứng với x thuộc D) gọi là tập giá trị của hàm số.
Chú ý:
+ Ta thường dùng kí hiệu f(x) để chỉ giá trị y tương ứng với x, nên hàm số còn được viết là y = f(x).
+ Khi một hàm số được cho bằng công thức mà không chỉ rõ tập xác định thì ta quy ước:
Tập xác định của hàm số y = f(x) là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa.
+ Một hàm số có thể được cho bởi hai hay nhiều công thức.
Ví dụ:
+ Hàm số có thể được cho bằng bảng dưới đây:
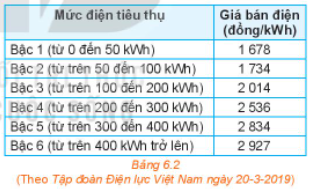
Với mỗi lượng điện tiêu thụ (kWh) thì sẽ có một số tiền phải trả tương ứng (nghìn đồng). Ta nói bảng trên biểu thị một hàm số.
+ Hàm số có thể được cho bằng công thức, ví dụ như: y = 2x – 1, y = x2, …. với biến số là x và y là hàm số của x.
+ Hàm số được cho bởi hai công thức như Nghĩa là với x ≤ ‒3 thì f(x) = ‒2x + 1, với x > ‒3 thì
+ Với hàm số y = f(x) = , tập xác định của hàm số là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa tức là có nghĩa, hay x ≠ 2.
Vậy tập xác định của hàm số này là D = ℝ\{2}.
2. Đồ thị hàm số
- Cho hàm số y = f(x) có tập xác định D.
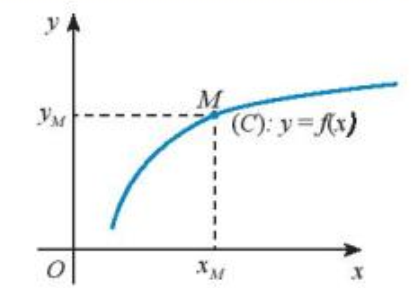
Trên mặt phẳng tọa độ Oxy, đồ thị (C) của hàm số là tập hợp tất cả các điểm M(x; y) với x ∈ D và y = f(x).
Chú ý: Điểm M(xM; yM) thuộc đồ thị hàm số y = f(x) khi và chỉ khi xM ∈ D và yM = f(xM).
 Ví dụ:
Ví dụ:
+ Cho hàm số y = f(x) = 2x – 1 có tập xác định D = ℝ.
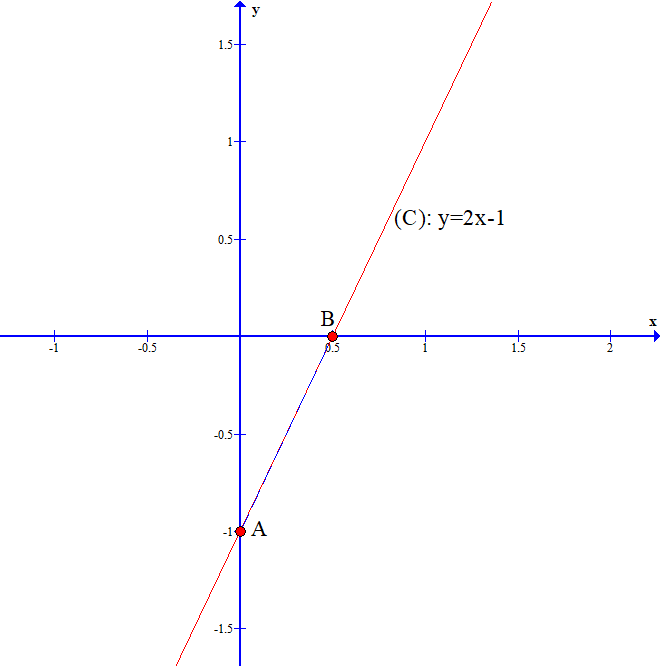
Trên mặt phẳng tọa độ Oxy, đồ thị (C) là đồ thị của hàm số y = f(x) = 2x – 1.
Khi thay x = 0 và y = ‒1 vào hàm số, ta được ‒1 = 2. 0 – 1 là mệnh đề đúng nên điểm A(0; ‒1) là điểm thuộc đồ thị (C).
Khi thay x = 0,5 và y = 0 vào hàm số, ta được 0 = 2. 0,5 – 1 là mệnh đề đúng nên điểm B(0,5; 0) là điểm thuộc đồ thị (C).
3. Hàm số đồng biến, hàm số nghịch biến
- Với hàm số y = f(x) xác định trên khoảng (a; b), ta nói:
+ Hàm số đồng biến trên khoảng (a; b) nếu
∀x1, x2 ∈ (a; b), x1 < x2 ⇒ f(x1) < f(x2).
+ Hàm số nghịch biến trên khoảng (a; b) nếu
∀x1, x2 ∈ (a; b), x1 < x2 ⇒ f(x1) > f(x2).
Nhận xét:
+ Khi hàm số đồng biến (tăng) trên khoảng (a; b) thì đồ thị của nó có dạng đi lên từ trái sang phải. Ngược lại, khi hàm số nghịch biến (giảm) trên khoảng (a; b) thì đồ thị của nó có dạng đi xuống từ trái sang phải.
Ví dụ:
+ Cho hàm số y = f(x) = 2x – 1 xác định trên ℝ.
Xét hai giá trị x1 = 1 và x2 = 2 đều thuộc ℝ, ta có:
f(x1) = f(1) = 2.1 – 1 = 1.
f(x2) = f(2) = 2.2 – 1 = 3.
Ta thấy x1 < x2 và f(x1) < f(x2) nên hàm số y = f(x) = 2x – 1 là hàm số đồng biến trên ℝ.
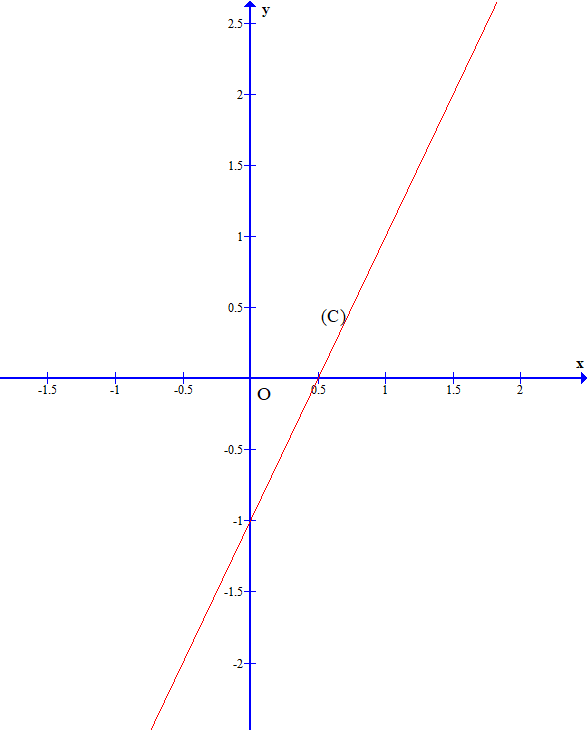
Ta thấy hàm số y = f(x) = 2x – 1 là hàm số đồng biến trên ℝ nên đồ thị của nó có dạng đi lên từ trái sang phải.
+ Cho hàm số y = f(x) = ‒ x + 2 xác định trên ℝ.
Xét 2 giá trị x1 = 1 và x2 = 2 đều thuộc ℝ, ta có:
f(x1) = f(1) = ‒1 + 2 = 1.
f(x2) = f(2) = ‒ 2 + 2 = 0.
Ta thấy x1 < x2 và f(x1) > f(x2) nên hàm số y = f(x) = ‒ x + 2 là hàm số nghịch biến trên ℝ.
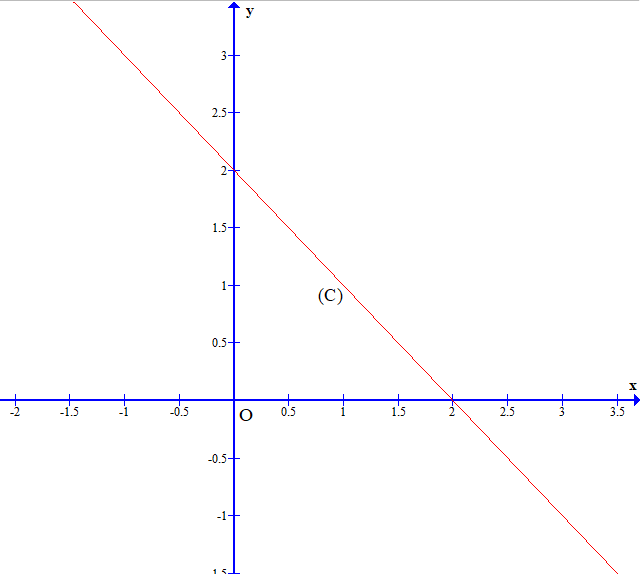
Ta thấy hàm số y = f(x) = ‒ x + 2 là hàm số nghịch biến trên ℝ nên đồ thị của nó có dạng đi xuống từ trái sang phải.
Ví dụ: Cho hàm số y = f(x) có tập xác định là [‒3; 3] và có đồ thị hàm số như hình vẽ.
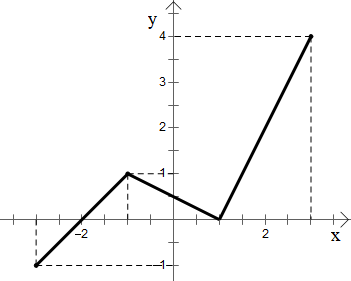
Tìm khoảng đồng biến, nghịch biến của hàm số trên.
Hướng dẫn giải
Dựa vào đồ thị nhận thấy:
- Đồ thị hàm số có dạng đi lên từ trái sang phải trên các khoảng (‒3; ‒1) và (1; 3) nên hàm số đồng biến trên khoảng (‒3; ‒1) và (1; 3);
- Đồ thị hàm số có dạng đi xuống từ trái sang phải trên khoảng (‒1; 1) nên hàm số nghịch biến trên khoảng (‒1; 1).
B. Bài tập tự luyện
Bài 1. Tìm tập xác định của các hàm số sau:
a) ;
b) .
Hướng dẫn giải
a) Biểu thức có nghĩa ⇔ 2x + 1 ≥ 0 ⇔ 2x ≥ ‒ 1 ⇔ x ≥ .
Vậy tập xác định D của hàm số này là D = .
b) Biểu thức có nghĩa ⇔ x + 3 ≠ 0 ⇔ x ≠ ‒3.
Vậy tập xác định D của hàm số này là D = ℝ\ {‒3}.
Bài 2. Xét tính đồng biến, nghịch biến của các hàm số sau:
a) y = f(x) = ‒ 2x + 2.
b) y = f(x) = x2 (trên khoảng (0;)
Hướng dẫn giải
a) Hàm số y = f(x) = ‒2x + 2 xác định trên ℝ.
Xét hai giá trị x1 = 1 và x2 = 2 đều thuộc ℝ, ta có:
f(x1) = f(1) = ‒2. 1 + 2 = 0.
f(x2) = f(2) = ‒2. 2 + 2 = ‒2.
Ta thấy x1 < x2 và f(x1) > f(x2) nên hàm số y = f(x) = ‒2x + 2 là hàm số nghịch biến trên ℝ.
b) Hàm số y = f(x) = x2 xác định trên khoảng (0; +∞).
Xét hai giá trị x1 = 1 và x2 = 2 đều thuộc khoảng (0; +∞), ta có:
f(x1) = f(1) = 12 = 1.
f(x2) = f(2) = 22 = 4.
Ta thấy x1 < x2 và f(x1) < f(x2) nên hàm số y = f(x) = x2 là hàm số đồng biến trên khoảng (0; +∞).
Bài 3. Tìm tập xác định và vẽ đồ thị hàm số:
y = f(x) = |2x + 3|.
Hướng dẫn giải
Tập xác định của hàm số D = ℝ.
Ta có: y = |2x + 3| =
Ta vẽ đồ thị y = 2x + 3 với (d1)
Ta có bảng sau:
|
x |
0 |
|
|
y = f(x) |
3 |
0 |
Suy ra đồ thị hàm số y = f(x) = 2x + 3 với là phần đồ thị nằm bên trên trục Ox và đi qua các điểm A(‒ ; 0) và B(0; 3).
Ta có đồ thị như sau:
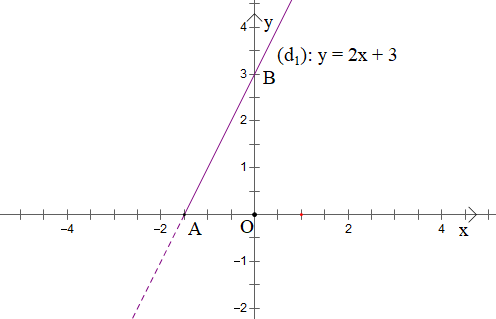
Tương tự ta có đồ thị hàm số y = f(x) = - 2x - 3 với x < - là phần đồ thị nằm bên trên trục Ox và đi qua các điểm C(-2; 1) và D(-3; 3).
Kết hợp 2 đồ thị ta có đồ thị hàm số y = |2x + 3| là phần đồ thị nét liền nằm trên trục Ox.
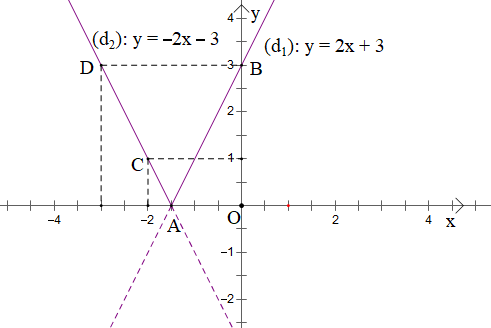
Bài 4. Một ô tô đi từ A đến B với đoạn đường AB = s (km). Ô tô di chuyển thẳng đều với vận tốc là 40 km/h. Gọi mốc thời gian là lúc ô tô bắt đầu xuất phát từ A, t là thời điểm ô tô đi ở vị trí bất kì trên đoạn AB. Hãy xác định hàm số biểu thị mối quan hệ giữa s và t, vẽ đồ thị hàm số đó và xét tính đồng biến, nghịch biến của hàm số từ đó rút ra nhận xét.
Hướng dẫn giải
Do thời gian luôn lớn hơn 0 nên tập xác định của hàm số ẩn t là D = (0; +∞)
Ta có công thức: Quãng đường = Vận tốc × Thời gian.
Ta có hàm số như sau: s = v. t = 40. t
Vẽ đồ thị hàm số s = 40t:
Ta có bảng sau:
|
t |
0,5 |
1 |
1,5 |
|
s = 40t |
20 |
40 |
60 |
Vậy các điểm có tọa độ (0,5; 20), (1; 40), (1,5; 60) thuộc đồ thị hàm số s = f(t).
Ta có đồ thị như sau:
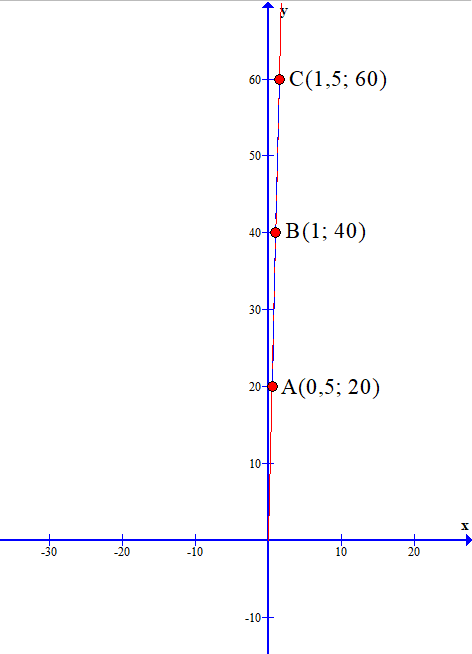
Ta thấy đồ thị hàm số đi lên từ trái sang phải nên đây là hàm số đồng biến trên (0; +∞).
Nhận xét: Trong di chuyển thẳng đều, thời gian luôn tỉ lệ thuận với quãng đường. Thời gian càng lâu thì quãng đường đi được càng lớn và ngược lại.
Xem thêm tóm tắt lý thuyết Toán lớp 10 sách Chân trời sáng tạo hay, chi tiết khác:
Lý thuyết Bài 2: Hàm số bậc hai
Lý thuyết Bài tập cuối chương 3
Lý thuyết Bài 1: Giá trị lượng giác của một góc từ 0° đến 180°
Xem thêm các chương trình khác:
- Soạn văn lớp 10 (hay nhất) – Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn lớp 10 – Chân trời sáng tạo
- Soạn văn lớp 10 (ngắn nhất) – Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn lớp 10 – Chân trời sáng tạo
- Giải sbt Ngữ văn lớp 10 – Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn lớp 10 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 10 – Chân trời sáng tạo
- Văn mẫu lớp 10 – Chân trời sáng tạo
- Giải Chuyên đề học tập Ngữ văn 10 – Chân trời sáng tạo
- Giải sgk Tiếng Anh 10 Friends Global – Chân trời sáng tạo
- Giải sbt Tiếng Anh 10 Friends Global – Chân trời sáng tạo
- Trọn bộ Từ vựng Tiếng Anh 10 Friends Global đầy đủ nhất
- Ngữ pháp Tiếng Anh 10 Friends Global
- Giải sgk Vật lí 10 – Chân trời sáng tạo
- Giải sbt Vật lí 10 – Chân trời sáng tạo
- Lý thuyết Vật lí 10 – Chân trời sáng tạo
- Giải Chuyên đề Vật lí 10 – Chân trời sáng tạo
- Giải sgk Hóa học 10 – Chân trời sáng tạo
- Lý thuyết Hóa học 10 – Chân trời sáng tạo
- Giải sbt Hóa học 10 – Chân trời sáng tạo
- Giải Chuyên đề Hóa học 10 – Chân trời sáng tạo
- Giải sgk Sinh học 10 – Chân trời sáng tạo
- Giải sbt Sinh học 10 – Chân trời sáng tạo
- Lý thuyết Sinh học 10 – Chân trời sáng tạo
- Giải Chuyên đề Sinh học 10 – Chân trời sáng tạo
- Giải sgk Lịch sử 10 – Chân trời sáng tạo
- Giải sbt Lịch sử 10 – Chân trời sáng tạo
- Giải Chuyên đề Lịch sử 10 – Chân trời sáng tạo
- Lý thuyết Lịch sử 10 – Chân trời sáng tạo
- Giải sgk Địa lí 10 – Chân trời sáng tạo
- Lý thuyết Địa Lí 10 - Chân trời sáng tạo
- Giải sbt Địa lí 10 – Chân trời sáng tạo
- Giải Chuyên đề Địa lí 10 – Chân trời sáng tạo
- Giải sgk Giáo dục Kinh tế và Pháp luật 10 – Chân trời sáng tạo
- Giải sbt Giáo dục Kinh tế và Pháp luật 10 – Chân trời sáng tạo
- Giải Chuyên đề Kinh tế và pháp luật 10 – Chân trời sáng tạo
- Lý thuyết KTPL 10 – Chân trời sáng tạo
- Giải sgk Hoạt động trải nghiệm 10 – Chân trời sáng tạo
- Giải sbt Hoạt động trải nghiệm 10 – Chân trời sáng tạo
- Giải sgk Giáo dục thể chất 10 – Chân trời sáng tạo
