Nội dung bài viết

    Xem thêm

    Lý thuyết Các phép toán trên tập hợp – Toán 10 Chân trời sáng tạo

    Với lý thuyết Toán lớp 10 Bài 3: Các phép toán trên tập hợp chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sách Chân trời sáng tạo sẽ giúp học sinh nắm vững kiến thức trọng tâm để học tốt môn Toán 10.

    1 2,267 03/01/2023
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Lý thuyết Toán 10 Bài 3: Các phép toán trên tập hợp - Chân trời sáng tạo

    A. Lý thuyết

    1. Hợp và giao của các tập hợp

    - Cho hai tập hợp A và B.

    Tập hợp các phần tử thuộc A hoặc thuộc B gọi là hợp của hai tập hợp A và B, kí hiệu A ∪ B.

    A ∪ B = {x| x ∈ A hoặc x ∈ B}.

    Tập hợp các phần tử thuộc cả hai tập hợp A và B gọi là giao của hai tập hợp A và B, kí hiệu A ∩ B.

    A ∩ B = {x | x ∈ A và x ∈ B}.

    Nhận xét:

    + Nếu A và B là hai tập hợp hữu hạn thì n(A ∪ B) = n(A) + n(B) – n(A ∩ B).

    + Đặc biệt, nếu A và B không có phần tử chung, tức A ∩ B = ∅, thì n(A ∪ B) = n(A) + n(B).

    Ví dụ 1.

    + Cho hai tập hợp S = {2; 3; 4; 5; 6; 7; 8; 9} và T = {4; 5; 6; 7}.

    Giao của 2 tập hợp là tập hợp M = S ∩ T = {4; 5; 6; 7}.

    + Cho hai tập hợp S = {1; 2; 3; 4} và T = {5; 6; 7}.

    Hợp của hai tập hợp S và T là tập hợp N = S ∪ T = {1; 2; 3; 4; 5; 6; 7}.

    2. Hiệu của hai tập hợp, phần bù của tập con

    - Cho hai tập hợp A và B.

    Tập hợp các phần tử thuộc A nhưng không thuộc B gọi là hiệu của A và B, kí hiệu A\B.

    A\B = {x | x ∈ A và x ∉ B}.

    Nếu A là tập con của E thì hiệu E\A gọi là phần bù của A trong E, kí hiệu CEA.

    Chú ý: Trong các chương sau, để tìm các tập hợp là hợp, giao, hiệu, phần bù của những tập con của tập số thực, ta thường vẽ sơ đồ trên trục số.

    Ví dụ: 2.

    + Cho hai tập hợp S = {2; 3; 4; 5; 6; 7; 8; 9} và T = {4; 5; 6; 7}.

    Hiệu của S và T là S\T = {2; 3; 8; 9}.

    Ta thấy T là tập con của S nên phần bù của T trong S chính là:

    CST = S\T = {2; 3; 8; 9}.

    + Xác định tập hợp: B = (7; 12] ∪ (‒∞; 9].

    Để xác định tập hợp B, ta vẽ sơ đồ sau đây:

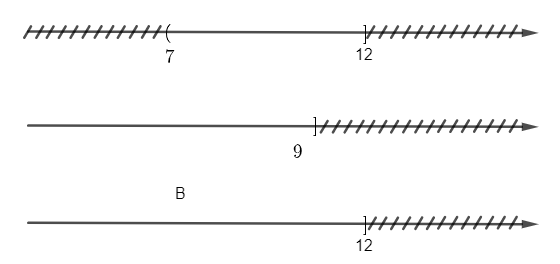
    Từ đó ta thấy, B = (‒∞; 12].

    B. Bài tập tự luyện

    Bài 1. Xác định tập hợp A ∩ B trong mỗi trường hợp sau:

    a) A = {x ∈ ℕ | x ⋮ 4, x < 30}, B = {x ∈ ℕ | x ⋮ 5, x < 30}.

    b) A = {x2 + 1 | x ∈ ℕ, x < 6}, B = {x3 | x ∈ ℕ, x < 5}.

    c) A = {x ∈ ℕ | x ⋮ 4, 5< x < 7}, B = {x1000 | x ∈ ℕ, x > 5}.

    Hướng dẫn giải

    a) Ta xác định các phần tử của tập hợp A và tập hợp B.

    A = {0; 4; 8; 12; 16; 20; 24; 28}.

    B = {0; 5; 10; 15; 20; 25}.

    Suy ra A ∩ B = {0; 20}.

    b) Ta xác định các phần tử của tập hợp A và tập hợp B.

    A = {1; 2; 5; 10; 17; 26}.

    B = {0; 1; 8; 27; 64}.

    Suy ra A ∩ B = {1}.

    c) Ta xác định các phần tử của tập hợp A và tập hợp B.

    A = ∅. Vậy A ∩ B = ∅.

    Bài 2. Cho U = {x ∈ ℕ | x < 20}, A = {x ∈ U | x là bội của 4}, B = {x ∈ U | x là ước của 12}. Xác định các tập hợp A\B, B\A, CUA, CUB, CU(A ∪ B), CU( A ∩ B).

    Hướng dẫn giải

    Ta xác định các phần tử của tập hợp U, A, B.

    U = {x ∈ ℕ | x < 20} = {0; 1; 2; 3; 4; …; 19}.

    A = {x ∈ U | x là bội của 4} = {0; 4; 8; 12; 16}.

    B = {x ∈ U | x là ước của 12} = {1; 2; 3; 4; 6; 12}.

    Khi đó ta có:

    A\B = {0; 8; 16}.

    B\A = {1; 2; 3; 6}.

    CUA = {1; 2; 3; 5; 6; 7; 9; 10; 11; 13; 14; 15; 17; 18; 19}.

    CUB = {0; 5; 7; 8; 9; 10; 11; 13; 14; 15; 16; 17; 18; 19}.

    A ∩ B = {4; 12}, A ∪ B = {0; 1; 2; 3; 4; 6; 8; 12; 16}.

    CU(A ∪ B) = {5; 7; 9; 10; 11; 13; 14; 15; 17; 18; 19}.

    CU( A ∩ B) = {1; 2; 3; 5; 6; 7; 8; 9; 10; 11; 13; 14; 15; 16; 17; 18; 19}.

    Bài 3. Xác định các tập hợp sau đây: 

    a) C = (7; 12] ∩ (-∞; 9].

    b) D = (7; 12] \ (-∞; 9].

    Hướng dẫn giải

    a) Để xác định tập C, ta vẽ sơ đồ sau đây: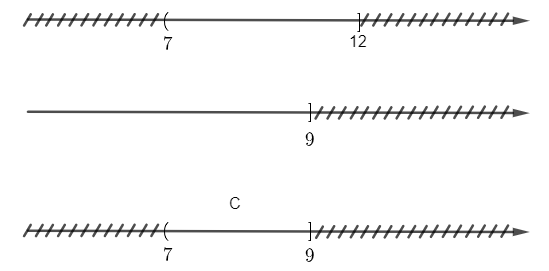

    Từ sơ đồ ta thấy, C = (7; 9].

    b) Để xác định tập D, ta vẽ sơ đồ sau đây:

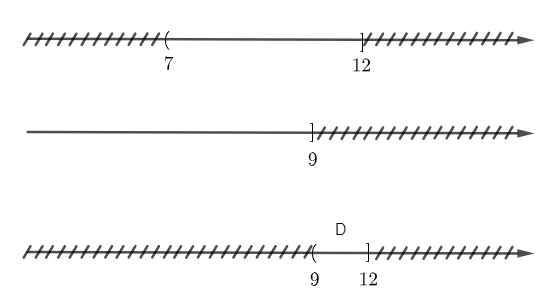    Từ sơ đồ ta thấy, D = (9; 12].

    Bài 4. Lớp 10A của trường có 33 học sinh, trong đó có 20 học sinh thích môn Toán, 18 học sinh thích môn Ngữ Văn và 10 học sinh thích cả môn Toán và Ngữ Văn. Hỏi lớp 10A có:

    a) Bao nhiêu học sinh thích ít nhất 1 trong 2 môn Toán và môn Ngữ Văn?

    b) Bao nhiêu học sinh không thích môn nào?

    Hướng dẫn giải

    a) Gọi A là tập hợp số học sinh thích môn Toán.

    B là tập hợp số học sinh thích môn Ngữ Văn.

    Số phần tử của A và B lần lượt là n(A) và n(B) thì n(A) = 20, n(B) = 18.

    Ta có:

    +) Tập hợp số học sinh thích cả môn Toán và Ngữ Văn là A ∩ B nên n(A ∩ B) = 10.

    +) Tập hợp số học sinh thích ít nhất 1 trong 2 môn Toán và môn Ngữ Văn là A ∪ B.

    Nên tổng số học sinh thích ít nhất 1 trong 2 môn Toán và môn Ngữ Văn là n(A ∪ B).

    Suy ra n(A ∪ B) = n(A) + n(B) ‒ n(A ∩ B) = 20 + 18 – 10 = 28.

    Vậy có 28 học sinh thích ít nhất 1 trong 2 môn Toán và môn Ngữ Văn.

    b) Số học sinh không thích môn học nào là: 33 – 28 = 5 (học sinh)

    Vậy có 5 học sinh không thích môn học nào trong hai môn Toán và môn Ngữ

    Xem thêm tóm tắt lý thuyết Toán lớp 10 sách Chân trời sáng tạo hay, chi tiết khác:

    Lý thuyết Bài tập cuối chương 1

    Lý thuyết Bài 1: Bất phương trình bậc nhất hai ẩn

    Lý thuyết Bài 2: Hệ bất phương trình bậc nhất hai ẩn

    Lý thuyết Bài tập cuối chương 2

    Lý thuyết Bài 1: Hàm số và đồ thị

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 2,267 03/01/2023
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: