Giải SBT Lí 11 Bài 11: Phương pháp giải một số bài toán về toàn mạch

Mục lục Giải SBT Lí 11 Bài 11. Phương pháp giải một số bài toán về toàn mạch

Bài 11.1 trang 29 SBT Lí 11: Cho mạch điện có sơ đồ như Hình 11.1, trong đó nguồn điện có suất điện động E = 15 V và điện trở trong r = 3 Ω, các điện trở R₁ = 9 Ω, R₂ = 8 Ω, R₃ = 10 Ω, vôn kế V có điện trở rất lớn.

Số chỉ của vôn kế là:

A. 5V    

B. 9V    

C. 10V    

D. 13,5V

Lời giải

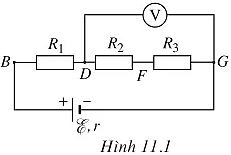
Mạch ngoài gồm ba điện trở nối tiếp:

R_N = R₁ + R₂ + R₃ = 9 + 8 +10 = 28 Ω

Cường độ dòng điện qua mạch chính:

$I=\frac{\text{E}}{R_N+r}=\frac{15}{28+3}\approx 0,5A$

Số chỉ của vôn kế: U_V = U₂₃ = I₂₃. R₂₃

Với I₂₃ = I = 0,5A

R₂₃ = R₂ + R₃ = 18Ω

⇒ U_V = 0,5 . 18 = 9V

Chọn đáp án B

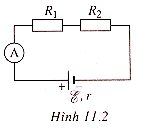
Bài 11.2 trang 29 SBT Lí 11: Cho mạch điện có sơ đồ như hình 11.2. Trong đó có các điện trở R₁ = 2Ω và R₂ = 1Ω nguồn điện có suất điện động là E = 3V và điện trở trong r = 1Ω. Điện trở của ampe kế và các dây nối không đáng kể.

Số chỉ của ampe kế trong mạch điện này là

A. 1A      

B. 3A       

C. 0,75A         

D. 1,5A

Lời giải:

Điện trở mạch ngoài:

R_N = R₁ + R₂ = 3Ω

Cường độ dòng điện chính trong mạch:

$I=\frac{\text{E}}{R_N+r}=\frac{3}{3+1}=0,75A$

Vậy số chỉ của Ampe kế trong mạch là 0,75A

Chọn đáp án C

Bài 11.3 trang 29 SBT Lí 11: Ba điện trở giống hệt nhau, mỗi điện trở 3Ω được mắc vào nguồn điện có suất điện động E và điện trở trong là r = 1Ω sao cho cường độ dòng trong mạch lớn nhất là 1,5A. Suất điện động của nguồn điện này là

A. 5V        

B. 4,5V      

C. 1,5V      

D. 3V

Lời giải

Cường độ dòng điện chính trong mạch:

$I=\frac{\text{E}}{R_N+r}=\frac{\text{E}}{R_N+1}$

I_max khi (R_N + 1)_min hay R_N min.

Vậy mạch ngoài gồm ba điện trở mắc song song:

$\frac{1}{R_{N\min }}=\frac{1}{R}+\frac{1}{R}+\frac{1}{R}=\frac{3}{R}$

$\Rightarrow R_{N\min }=\frac{R}{3}=\frac{3}{3}=1\Omega$

Vậy suất điện động chạy trong mạch:

E = 1,5 . (1+1) = 3V

Chọn đáp án D

Bài 11.4 trang 29 SBT Lí 11: Một dây hợp kim có điện trở là R = 5Ω được mắc vào hai cực của một pin điện hoá có suất điện động và điện trở trong là E = 1,5 V, r = 1 Ω. Điện trở của các dây nối là rất nhỏ.

a) Tính lượng hoá năng được chuyển hoá thành điện năng trong 5 phút.

b) Tính nhiệt lượng toả ra ở điện trở R trong khoảng thời gian đã cho trên đây.

c) Giải thích sự khác nhau giữa các kết quả tính được ở câu a và b trên đây.

Lời giải

a) Đổi t = 5 phút = 300 giây

Cường độ dòng điện chạy trong mạch là:

$I=\frac{\text{E}}{R_N+r}=\frac{1,5}{5+1}=0,25A$

Lượng hoá năng được chuyển hoá thành điện năng khi đó là:

A_hoá = EIt = 112,5 J

b) Nhiệt lượng toả ra ở điện trở R khi đó là:

Q = I²R.t = 93,75 J.

c) Lượng hoá năng A_hóa được chuyển hoá thành điện năng và bằng tổng nhiệt lượng Q toả ra ở điện trở R và nhiệt lượng tỏa ra trong trên điện trở trong r của nguồn. Vì vậy nhiệt lượng Q chỉ là một phần của hóa năng A_hoá.

Bài 11.5 trang 30 SBT Lí 11: Cho một nguồn điện có suất điện động E = 24 V và điện trở trong r = 6 Ω.

a) Có thể mắc nhiều nhất bao nhiêu bóng đèn loại 6 V - 3 W vào nguồn điện đã cho trên đây để các đèn sáng bình thường? Vẽ sơ đồ cách mắc.

b) Nếu chỉ có 6 bóng đèn loại trên đây thì phải mắc chúng vào nguồn điện đã cho theo sơ đồ nào để các đèn sáng bình thường? Trong các cách mắc này thì cách nào lợi hơn? Vì sao?

Lời giải

a) Vì các bóng đèn cùng loại nên phải được mắc thành các dãy song song, mỗi dãy gồm cùng số đèn mắc nối tiếp. Bằng cách đó, dòng điện chạy qua mỗi đèn mới có cùng cường độ bằng cường độ định mức.

Giả sử các đèn được mắc thành x dãy song song, mỗi dãy gồm y đèn mắc nối tiếp theo sơ đồ như trên Hình 11.1G.

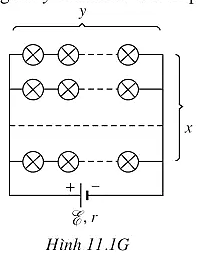
Các trị số định mức của đèn là:

U_đ = 6V; P_đ = 3 W; I_đ = 0,5 A.

Khi đó hiệu điện thế mạch ngoài là:

U = yU_đ = 6y

Dòng điện mạch chính có cường độ là:

I = xI_đ = 0,5x

Theo định luật Ôm ta có:

U = E – Ir

thay các trị số đã có ta được phương trình:

2y + x = 8 (1)

Kí hiệu số bóng đèn là n = xy và sử dụng bất đẳng thức Cô-si ta có:

2y + x ≥ 2.$\sqrt{xy}$  (2)

Kết hợp (1) và (2) ta tìm được:

n = xy ≤ 8.

Vậy có thể mắc nhiều nhất là n = 8 bóng đèn loại này.

Dấu bằng xảy ra với bất đẳng thức (2) khi 2y = x và với xy = 8.

Từ đó suy ra x = 4 và y = 2, nghĩa là trong trường hợp này phải mắc 8 bóng đèn thành 4 dãy song song, mỗi dãy gồm 2 bóng đèn mắc nối tiếp như sơ đồ Hình 11.2G.

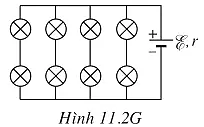
b) Xét trường hợp chỉ có 6 bóng đèn loại đã cho, ta có: xy = 6

Kết hợp với phương trình (1) trên đây ta tìm được:

x = 2 và do đó y = 3 hoặc x = 6 và do đó y = 1.

Nghĩa là có hai cách mắc 6 bóng đèn loại này:

- Cách thứ nhất: Mắc thành 2 dãy song song, mỗi dãy có 3 đèn nối tiếp như sơ đồ Hình 11.3Ga.

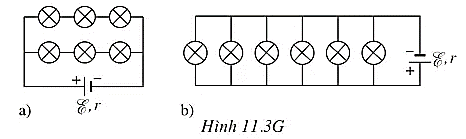
- Cách thứ hai: Mắc thành 6 dãy song song, mỗi dãy 1 đèn như Hình 11.3Gb.

Theo cách mắc thứ nhất (x = 2, y = 3) thì hiệu suất của nguồn là:

$H_1=\frac{U_1}{\text{E}}=\frac{6.3}{24}=0,75=75\%$

Theo cách mắc thứ hai (x = 6, y = 1) thì hiệu suất của nguồn là:

$H_2=\frac{U_2}{\text{E}}=\frac{6.1}{24}=0,25=25\%$

Vậy cách mắc thứ nhất có lợi hơn vì có hiệu suất lớn hơn nên năng vô ích nhỏ hơn.

Bài 11.6 trang 30 SBT Lí 11: Có N₁ bóng đèn cùng loại 3 V - 3 W và N₂ nguồn điện có cùng suất điện động E₀ = 4 V và điện trở trong r₀ = 1 Ω được mắc thành bộ nguồn hỗn hợp đối xứng.

a) Nếu số bóng đèn là N₁ = 8 thì cần số nguồn ít nhất (N₂ min) là bao nhiêu để các đèn này sáng bình thường? Vẽ sơ đồ các cách mắc nguồn và đèn khi đó và tính hiệu suất của bộ nguồn trong từng trường hợp.

b) Nếu số nguồn là N₂ = 15 thì có thể thắp sáng bình thường số đèn lớn nhất (N₁ max) là bao nhiêu? Vẽ sơ đồ tất cả các cách mắc nguồn và đèn khi đó và tính hiệu suất của bộ nguồn đối với từng cách mắc đó.

Lời giải

a) Để các đèn cùng loại sáng bình thường thì các đèn thành các dãy song song, mỗi dãy có cùng một số đèn mắc nối tiếp.

Gọi số dãy các đèn mắc song song là x và số đèn mắc nối tiếp là y thì theo đầu bài ta xét trường hợp có tổng số đèn là:

N₁ = xy = 8.

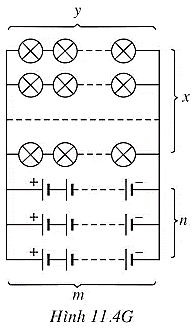
Giả sử bộ nguồn hỗn hợp đối xứng gồm n dãy song song và mỗi dãy gồm m nguồn được mắc nối tiếp (Hình 11.4G).

Khi đó bộ nguồn gồm N₂ = mn nguồn và có suất điện động là: E_b = mE₀ = 4m và có điện trở trong là:

$r_b=\frac{m{r}_0}{n}=\frac{m}{n}$

Các trị số định mức của đèn là:

U_Đ = 3 V; P_Đ = 3 W; I_Đ = P_Đ : U_Đ = 1 A.

Cường độ dòng điện mạch chính là:

I = xI_Đ = x

Hiệu điện thế mạch ngoài là:

U = yU_Đ = 3y

Theo định luật Ôm ta có:

U = E_b – Ir_b hay  $3y=4m-\frac{xm}{n}$

Từ đó suy ra: 3yn + xm = 4mn (1)

Sử dụng bất đẳng thức Cô-si ta có:

$3yn+xm\ge 2.\sqrt{3mnxy}\left(2\right)$

Kết hợp (1) và (2) trong đó chú ý là

N₁ = xy = 8 và N₂ = mn ta tìm được: N₂ ≥ 6

Vậy số nguồn ít nhất tà N₂ (min) = 6 để thắp sáng bình thường bóng đèn.

Để vẽ được sơ đồ các cách mắc nguồn và đèn cho trường hợp này ta lại xét phương trình (1) trên đây, trong đó thay trị số N₂ = mn = 6;$y=\frac{N_1}{x}=\frac{8}{x}$

ta đi tới phương trình: yn² – 8n + 2x = 0

Phương trình này có nghiệm kép (Δ’ = 0) là:  $n=\frac{4}{y}$

Chú ý rằng x, y, n và m đều là số nguyên, dương nên ta có bảng các trị số này như sau:

y	x	n	m
2	4	2	3
4	2	1	6

Như vậy trong trường hợp này chỉ có hai cách mắc các nguồn và các bóng đèn là:

- Cách một: Bộ nguồn gồm n = 2 dãy song song, mỗi dãy gồm m = 3 nguồn mắc nối tiếp và các bóng đèn được mắc thành x = 4 dãy song song với mỗi dãy gồm y = 2 bóng đèn mắc nối tiếp (Hình 11.5Ga).

Cách mắc này có hiệu suất là:  $H_1=\frac{6}{12}=0,5=50\%$

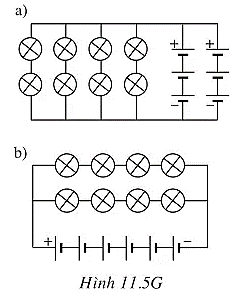
- Cách hai: Bộ nguồn gồm n = 1 dãy gồm m = 6 nguồn mắc nối tiếp và các bóng đèn được mắc thành X = 2 dãy song song với mỗi dãy gồm y = 4 bóng đèn mắc nối tiếp (Hình 11.5Gb).

Cách mắc này có hiệu suất là:

$H_2=\frac{12}{24}=0,5=50\%$

b) Nếu số nguồn là N₂ = mn = 15 và với số đèn là N₁ = xy

Ta cũng có phương trình (1) và bất đẳng thức (2) trên đây.

Kết quả là trong trường hợp này ta có:

$3yn+xm=4mn\ge 2.\sqrt{3mnxy}$

hay  $60\ge 2.\sqrt{45N_1}$

Từ đó suy ra: N₁ ≤ 20. Vậy với số nguồn là N₂ = 15 thì có thể thắp sáng bình thường số đèn lớn nhất là N₁ = 20.

Để tìm được cách mắc nguồn và đèn trong trường hợp này

Ta có xỵ = 20 hay $y=\frac{20}{x}$

Thay giá trị này vào phương trình (1) ta đi tới phương trình:

mx² – 60x + 60n = 0

Phương trình này có nghiêm kép (Δ' = 0) là: $x=\frac{30}{m}$

Chú ý rằng x, y, n và m đều là số nguyên, dương nên ta có bảng các trị số này như sau:

m	n	x	y
3	5	10	2
15	1	2	10

Như vậy trong trường hợp này chỉ có hai cách mắc các nguồn và các bóng đèn là:

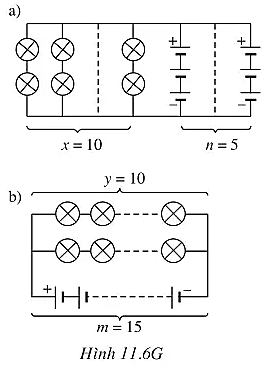
- Cách một: Bộ nguồn gồm n = 5 dãy song song, mỗi dãy gồm m - 3 nguồn mắc nối tiếp và các bóng đèn được mắc thành x = 10 dãy song song với mỗi dãy gồm y = 2 bóng đèn mắc nối tiếp (Hình 11.6Ga).

Cách mắc này có hiệu suất là: $H_1=\frac{6}{12}=0,5=50\%$

- Cách hai: Bộ nguồn gồm n = 1 dãy có m = 15 nguồn mắc nối tiếp và các bóng đèn được mắc thành x = 2 dãy song song với mỗi dãy gồm y = 10 bóng đèn mắc nối tiếp (Hình 11.6Gb).

Cách mắc này có hiệu suất là:$H_2=\frac{30}{60}=0,5=50\%$

Xem thêm lời giải bài tập Vật lí lớp 11 hay, chi tiết khác:

Bài tập cuối chương 2

Bài 13: Dòng điện trong kim loại

Bài 14: Dòng điện trong chất điện phân

Bài 15: Dòng điện trong chất khí

Bài 16: Dòng điện trong chân không

Xem thêm tài liệu Vật lí lớp 11 hay, chi tiết khác:

Lý thuyết Phương pháp giải một số bài toán về toàn mạch

Trắc nghiệm Phương pháp giải một số bài toán về mạch có đáp án