Cho tam giác ABC vuông tại A. Khẳng định nào sau đây là sai

Lời giải bài 10 trang 102 SBT Toán 10 Tập 1 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán lớp 10 Tập 1.

1 1,117 12/11/2024

Trang trước

Trang sau

Giải SBT Toán lớp 10 Bài tập cuối chương 5

Bài 10 trang 102 SBT Toán 10 Tập 1: Cho tam giác ABC vuông tại A. Khẳng định nào sau đây là sai?

Sách bài tập Toán 10 Bài tập cuối chương 5 - Chân trời sáng tạo (ảnh 1)

Đáp án đúng là D

*Lời giải:

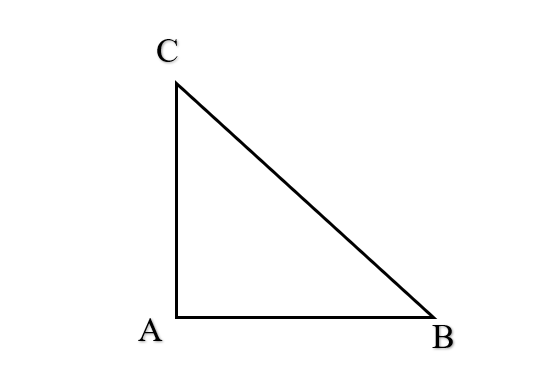
Do AB ⊥ AC nên

Ta lại có (vì $\hat{B}$ là góc nhọn nên cos $\hat{B}$ > 0). Do đó $\vec{AB} . \vec{AC} < \vec{BA} . \vec{BC} $ .

Khẳng định A đúng.

$(\vec{AC}, \vec{CB}) = (- \vec{CA}, \vec{CB}) = - (\vec{CA}, \vec{CB})$ là góc tù nên $\vec{AC} . \vec{CB} = \vec{|AC|} . |\vec{CB}| . \cos (\vec{AC} . \vec{CB})$ < 0;

$(\vec{AC} . \vec{BC})$ là góc nhọn nên $\vec{AC} . \vec{BC} = |\vec{AC}| . \vec{|BC|} . \cos (\vec{AC} . \vec{BC})$ > 0. Suy ra $\vec{AC} . \vec{CB} < \vec{AC} . \vec{BC} $ . Khẳng định B đúng.

$(\vec{AB}, \vec{BC}) = (- \vec{B A}, \vec{BC}) = - (\vec{B A}, \vec{BC})$ là góc tù nên $\vec{AB} . \vec{BC}$ < 0; $(\vec{CA} . \vec{CB})$ là góc nhọn nên $\vec{CA} . \vec{CB}$ > 0. Suy ra $\vec{AB} . \vec{BC} < \vec{CA} . \vec{CB}$ . Khẳng định C đúng.

$(\vec{AC} . \vec{BC})$ là góc nhọn nên $\vec{AC} . \vec{BC}$ > 0; $(\vec{BC} . \vec{AB})$ là góc tù nên $\vec{BC} . \vec{AB}$ < 0. Suy ra $\vec{AC} . \vec{BC} > \vec{BC} . \vec{AB}$ .

*Phương pháp giải:

- Sử dụng: Tích vô hướng của hai vectơ

Cho hai vectơ $\vec{a}$ và $\vec{b}$ đều khác $\vec{0}$ .

Tích vô hướng của $\vec{a}$ và $\vec{b}$ là một số, kí hiệu là $\vec{a}$ . $\vec{b}$ , được xác định bởi công thức:

$\vec{a}$ . $\vec{b}$ = | $\vec{a}$ |.| $\vec{b}$ |.cos( $\vec{a}$ , $\vec{b}$ ).

Để xét xem các đáp án có giá trị tích vô hướng 2 vectơ là góc tù/nhọn hay vuông

*Lý thuyết cần nắm và các dạng bài về vectơ:

Định nghĩa vectơ: Vectơ là một đoạn thẳng có hướng, nghĩa là đã chỉ ra điểm đầu và điểm cuối.

Hai vectơ cùng phương, cùng hướng

Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

Nhận xét:

+ Hai vectơ cùng phương chỉ có thể cùng hướng hoặc ngược hướng.

+ Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi hai vectơ $\vec{A B}$ và $\vec{A C}$ cùng phương.

Tổng hợp lý thuyết Toán 10 Chương 5 Chân trời sáng tạo (ảnh 4)

Tổng của hai vectơ

Cho hai vectơ $\vec{a}$ và $\vec{b}$ . Từ một điểm A tùy ý, lấy hai điểm B, C sao cho $\vec{A B} = \vec{a}, \vec{B C} = \vec{b}$ . Khi đó $\vec{A C}$ được gọi là tổng của hai vectơ $\vec{a}$ và $\vec{b}$ và được kí hiệu là $\vec{a} + \vec{b}$ .

Vậy $\vec{a} + \vec{b} = \vec{A B} + \vec{B C} = \vec{A C}$ .

Phép toán tìm tổng của hai vectơ được gọi là phép cộng vectơ.

Quy tắc ba điểm

Với ba điểm M, N, P, ta có $\vec{M N} + \vec{N P} = \vec{M P}$ .

Tổng hợp lý thuyết Toán 10 Chương 5 Chân trời sáng tạo (ảnh 9)

Chú ý: Khi cộng vectơ theo quy tắc ba điểm, điểm cuối của vectơ thứ nhất phải là điểm đầu của vectơ thứ hai.

Quy tắc hình bình hành

Nếu OACB là hình bình hành thì ta có $\vec{O A} + \vec{O B} = \vec{O C}$ .

Tổng hợp lý thuyết Toán 10 Chương 5 Chân trời sáng tạo (ảnh 10)

Tính chất của phép cộng các vectơ

Phép cộng vectơ có các tính chất sau:

+ Tính chất giao hoán: $\vec{a} + \vec{b} = \vec{b} + \vec{a}$ ;

+ Tính chất kết hợp: $(\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c})$ ;

+ Với mọi vectơ $\vec{a}$ , ta luôn có: $\vec{a} + \vec{0} = \vec{0} + \vec{a} = \vec{a}$ .

Chú ý: Từ tính chất kết hợp, ta có thể xác định được tổng của ba vectơ $\vec{a}, \vec{b}, \vec{c}$ , kí hiệu là $\vec{a} + \vec{b} + \vec{c}$ với $\vec{a} + \vec{b} + \vec{c} = (\vec{a} + \vec{b}) + \vec{c}$ .

+Cho vectơ tùy ý $\vec{a} = \vec{A B}$ .

Ta có $\vec{a} + (- \vec{a}) = \vec{A B} + (- \vec{A B}) = \vec{A B} + \vec{B A} = \vec{A A} = \vec{0}$ .

Tổng hai vectơ đối nhau luôn bằng vectơ-không: $\vec{a} + (- \vec{a}) = \vec{0}$ .

Hiệu của hai vectơ

Cho hai vectơ $\vec{a}$ và $\vec{b}$ . Hiệu của hai vectơ $\vec{a}$ và $\vec{b}$ là vectơ $\vec{a} + (- \vec{b})$ và kí hiệu là $\vec{a} - \vec{b}$ .

Phép toán tìm hiệu của hai vectơ được gọi là phép trừ vectơ.

Chú ý: Cho ba điểm O, A, B, ta có: $\vec{O B} - \vec{O A} = \vec{A B}$ .

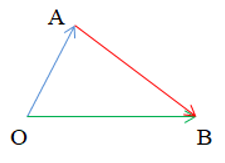
Tổng hợp lý thuyết Toán 10 Chương 5 Chân trời sáng tạo (ảnh 13)

Tích vô hướng của hai vectơ

Cho hai vectơ $\vec{a}$ và $\vec{b}$ đều khác $\vec{0}$ .

Tích vô hướng của $\vec{a}$ và $\vec{b}$ là một số, kí hiệu là $\vec{a}$ . $\vec{b}$ , được xác định bởi công thức:

$\vec{a}$ . $\vec{b}$ = | $\vec{a}$ |.| $\vec{b}$ |.cos( $\vec{a}$ , $\vec{b}$ ).

Chú ý:

a) Trường hợp có ít nhất một trong hai vectơ $\vec{a}$ và $\vec{b}$ bằng $\vec{0}$ , ta quy ước $\vec{a}$ . $\vec{b}$ = 0.

b) Với hai vectơ $\vec{a}$ và $\vec{b}$ , ta có $\vec{a} ⊥ \vec{b} \Leftrightarrow \vec{a} . \vec{b} = 0$ .

c) Khi $\vec{a} = \vec{b}$ thì tích vô hướng $\vec{a} . \vec{b}$ được kí hiệu là ${\vec{a}}^{2}$ và được gọi là bình phương vô hướng của vectơ $\vec{a}$ .

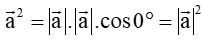
Ta có Tổng hợp lý thuyết Toán 10 Chương 5 Chân trời sáng tạo (ảnh 17) . Vậy bình phương vô hướng của một vectơ luôn bằng bình phương độ dài của vectơ đó.

Chú ý: Trong Vật lí, tích vô hướng của $\vec{F}$ và $\vec{d}$ biểu diễn công A sinh bởi lực $\vec{F}$ khi thực hiện độ dịch chuyển $\vec{d}$ . Ta có công thức: A= $\vec{F}$ . $\vec{d}$ .