Nội dung bài viết

    Xem thêm

    Sách bài tập Toán 10 Bài 1 (Chân trời sáng tạo): Khái niệm vectơ

    Với giải sách bài tập Toán 10 Bài 1: Khái niệm vectơ sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 Bài 1.

    1 1,667 30/12/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Giải sách bài tập Toán lớp 10 Bài 1: Khái niệm vectơ - Chân trời sáng tạo

    Giải SBT Toán 10 trang 91 Tập 1

    Bài 1 trang 91 SBT Toán 10 Tập 1: Bạn hãy tìm sự khác biệt giữa hai đại lượng sau:

    - Chiếc xe máy có giá tiền là 30 triệu đồng.

    - Chiếc thuyền chạy với vận tốc là 30 km/h theo hướng tây nam.

    Lời giải:

    - Chiếc xe máy có giá tiền là 30 triệu đồng: đại lượng vô hướng.

    - Chiếc thuyền chạy với vận tốc là 30 km/h theo hướng tây nam: đại lượng chỉ rõ giá trị và hướng.

    Bài 2 trang 91 SBT Toán 10 Tập 1: Trong các đại lượng sau, đại lượng nào cần được biểu diễn bởi vectơ?

    Nhiệt độ, lực, thể tích, tuổi, độ dịch chuyển, vận tốc.

    Lời giải:

    Các đại lượng cần được biểu diễn bởi vectơ: lực, độ dịch chuyển, vận tốc bởi đây là những đại lượng có hướng.

    Bài 3 trang 91 SBT Toán 10 Tập 1: Cho hình thang ABCD với hai đáy là AB, CD và có hai đường chéo cắt nhau tại O.

    a) Gọi tên hai vectơ cùng hướng với AO→.

    b) Gọi tên hai vectơ ngược hướng với AB→.

    Lời giải:

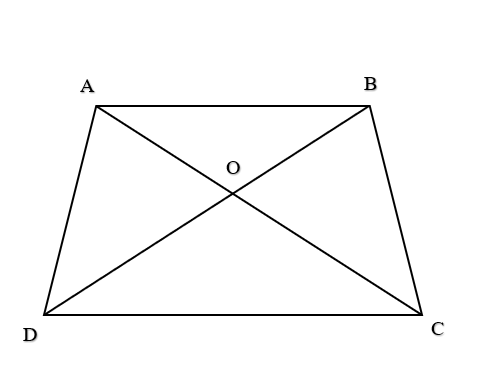
    Sách bài tập Toán 10 Bài 1: Khái niệm vectơ - Chân trời sáng tạo (ảnh 1)

    a) Hai vectơ cùng hướng với AO→: AC→ và OC→.

    b) Hai vectơ ngược hướng với AB→: BA→ và CD→.

    Bài 4 trang 91 SBT Toán 10 Tập 1: Cho hình thoi ABCD cạnh bằng a có tâm O và BAD^ = 60°.

    a) Tìm trong hình hai vectơ bằng nhau và có độ dài bằng a32.

    b) Tìm trong hình hai vectơ đối nhau và có độ dài bằng a3.

    Lời giải:

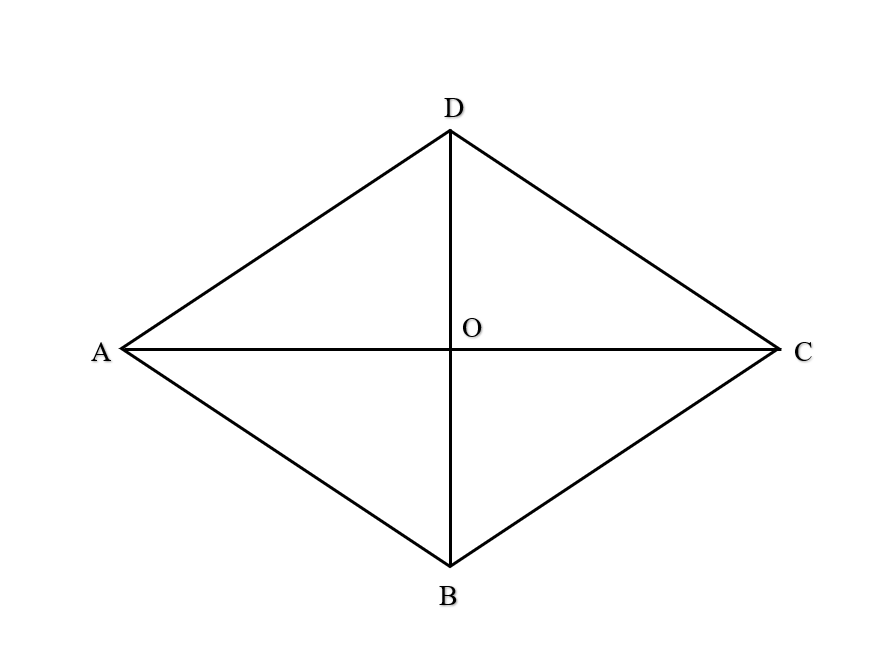
    Sách bài tập Toán 10 Bài 1: Khái niệm vectơ - Chân trời sáng tạo (ảnh 1)

    a) Ta có hình thoi ABCD có cạnh a. AO là tia phân giác của BAD^ ( tính chất hình thoi ) ⇒ DAO^ = 30°.

    AC ⊥ BD ( tính chất hình thoi ) ⇒ AOD^ = 90° ⇒ Tam giác AOD vuông tại O.

    Xét tam giác AOD vuông tại O: cosDAO^ =  cos30° = AOAD ⇒ AO = a. cos30° = a32.

    Hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường ( tính chất hình thoi )

    ⇒ AO = OC = a32.

    Vậy ta có hai vectơ AO→ và OC→ bằng nhau và có độ dài bằng a32.

    b) Ta có AC = AO + OC = a3.

    Vậy ta có hai vectơ AC→ và CA→ đối nhau và có độ dài a3.

    Bài 5 trang 91 SBT Toán 10 Tập 1: Cho hình chữ nhật ABCD có O là giao điểm hai đường chéo. Hãy chỉ ra một cặp vectơ:

    a) cùng hướng;

    b) ngược hướng;

    c) bằng nhau.

    Lời giải:

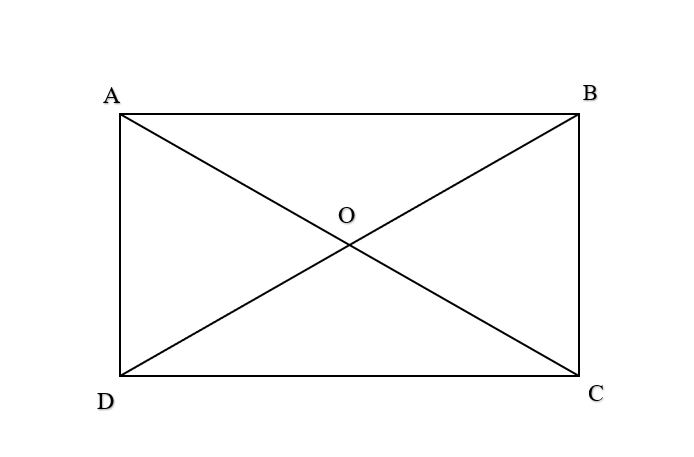
    Sách bài tập Toán 10 Bài 1: Khái niệm vectơ - Chân trời sáng tạo (ảnh 1)

    a) AO→ cùng hướng với AC→.

    b) DO→ ngược hướng với BD→.

    c) AB→=DC→ ( do có cùng hướng và AB = DC ).

    Bài 6 trang 91 SBT Toán 10 Tập 1: Gọi O là tâm của hình bát giác đều ABCDEFGH.

    a) Tìm hai vectơ khác 0​→ và cùng hướng với OA​→.

    b) Tìm vectơ bằng vectơ BD​→.

    Lời giải:

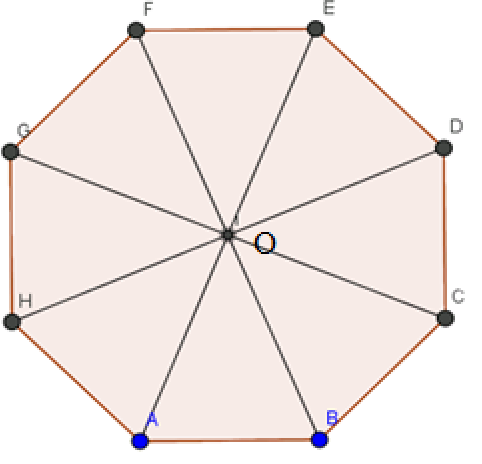
    Sách bài tập Toán 10 Bài 1: Khái niệm vectơ - Chân trời sáng tạo (ảnh 1)

    a) Hai vectơ khác 0​→ và cùng hướng với OA​→: EO​→, EA​→.

    b) Ta có: DOB^=28.360°=90°⇒ DH vuông góc với FB.

    Xét tứ giác FDBH: Hai đường chéo DH và FB vuông góc với nhau tại O là trung điểm của mỗi đường nên FDBH là hình thoi. ( DHNB hình thoi )

    Lại có FB = DH ( do đều là đường chéo của bát giác đều ) nên FDBH là hình vuông. (DHNB hình vuông )

    ⇒ HF = BD và HF // BD.

    Như vậy ta có vectơ bằng vectơ BD​→ là HF​→.

    Xem thêm lời giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

    Bài 2: Hàm số bậc hai

    Bài tập cuối chương 3

    Bài 1: Giá trị lượng giác của 1 góc từ 0° đến 180°

    Bài 2: Định lí côsin và định lí sin

    Bài tập cuối chương 4

    Xem thêm tài liệu Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

    Lý thuyết Bài 1: Khái niệm vectơ

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,667 30/12/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: