Bài 7 trang 13 Toán 11 Tập 1 | Chân trời sáng tạo Giải Toán 11
Lời giải Bài 7 trang 13 Toán 11 Tập 1 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 Tập 1.
Giải Toán 11 Bài 1: Góc lượng giác
Bài 7 trang 13 Toán 11 Tập 1: Trên đường tròn lượng giác hãy biểu diễn các góc lượng giác có số đo có dạng là:
a) π2+kπ(k∈ℤ);
b) kπ4(k∈ℤ).
Lời giải:
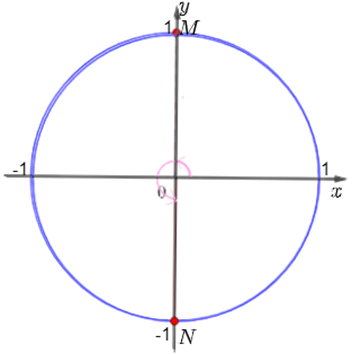
a) Với k = 0 thì có góc lượng giác có số đo góc là π2, được biểu diễn bởi điểm M;
Với k = 1 thì có góc lượng giác có số đo góc là π2+π=3π2, được biểu diễn bởi điểm N;
Với k = 2 thì có góc lượng giác có số đo góc là π2+2π nên cũng được biểu diễn bởi điểm M;
Với k = 3 thì có góc lượng giác có số đo góc là π2+3π=3π2+2π nên cũng được biểu diễn bởi điểm N.
Vậy với k chẵn thì các góc lượng giác có số đo dạng π2+kπ(k∈ℤ) được biểu diễn bởi điểm M, với k lẻ thì các góc lượng giác có số đo dạng π2+kπ(k∈ℤ) được biểu diễn bởi điểm N khi đó ta có hình vẽ sau:
b) Với k = 0 thì có góc lượng giác có số đo góc là 0, được biểu diễn bởi điểm A;
Với k = 1 thì có góc lượng giác có số đo góc là π4, được biểu diễn bởi điểm M;
Với k = 2 thì có góc lượng giác có số đo góc là 2π4=π2 được biểu diễn bởi điểm B;
Với k = 3 thì có góc lượng giác có số đo góc là 3π4 được biểu diễn bởi điểm N;
Với k = 4 thì có góc lượng giác có số đo góc là 4π4=π được biểu diễn bởi điểm A’;
Với k = 5 thì có góc lượng giác có số đo góc là 5π4 được biểu diễn bởi điểm M’;
Với k = 6 thì có góc lượng giác có số đo góc là 6π4=3π2 được biểu diễn bởi điểm B’;
Với k = 7 thì có góc lượng giác có số đo góc là 7π4 được biểu diễn bởi điểm N’;
Với k = 8 thì có góc lượng giác có số đo góc là 8π4=2π+0 nên được biểu diễn bởi điểm A;
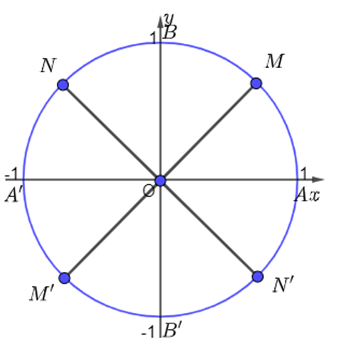
Vậy các góc lượng giác có số đo dạng π2+kπ(k∈ℤ) được biểu diễn bởi các điểm A, M, B, N, A’, M’, B’, N’. Khi đó ta có hình vẽ sau:
Xem thêm lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Hoạt động khám phá 2 trang 9 Toán 11 Tập 1: Cho Hình 7: a) Xác định số đo các góc lượng giác (Oa, Ob), (Ob, Oc) và (Oa, Oc)...
Thực hành 2 trang 11 Toán 11 Tập 1: Hoàn thành bảng chuyển đổi đơn vị đo của các góc sau đây...
Bài 1 trang 12 Toán 11 Tập 1: Đổi số đo của các góc dưới đây sang radian: a) 38°; b) – 115°; c) ...
Bài 2 trang 12 Toán 11 Tập 1: Đổi số đo của các góc sau đây sang độ: a) ; b) – 5; c) ...
Bài 3 trang 12 Toán 11 Tập 1: Biểu diễn các góc lượng giác sau trên đường tròn lượng giác: a) ; b) ; c) – 765°....
Xem thêm lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Giá trị lượng giác của một góc lượng giác
Bài 3: Các công thức lượng giác
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Chân trời sáng tạo (hay nhất)
- Văn mẫu lớp 11 - Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn 11 – Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn lớp 11 - Chân trời sáng tạo
- Giải SBT Ngữ văn 11 – Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Ngữ văn 11 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Chân trời sáng tạo
- Soạn văn 11 Chân trời sáng tạo (ngắn nhất)
- Giải sgk Tiếng Anh 11 – Friends Global
- Giải sbt Tiếng Anh 11 - Friends Global
- Trọn bộ Từ vựng Tiếng Anh 11 Friends Global đầy đủ nhất
- Bài tập Tiếng Anh 11 Friends Global theo Unit có đáp án
- Giải sgk Vật lí 11 – Chân trời sáng tạo
- Lý thuyết Vật lí 11 – Chân trời sáng tạo
- Giải sbt Vật lí 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Vật lí 11 – Chân trời sáng tạo
- Giải sgk Hóa học 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Hóa học 11 – Chân trời sáng tạo
- Lý thuyết Hóa 11 - Chân trời sáng tạo
- Giải sbt Hóa học 11 – Chân trời sáng tạo
- Giải sgk Sinh học 11 – Chân trời sáng tạo
- Lý thuyết Sinh học 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Sinh học 11 – Chân trời sáng tạo
- Giải sbt Sinh học 11 – Chân trời sáng tạo
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Chân trời sáng tạo
- Lý thuyết Kinh tế pháp luật 11 – Chân trời sáng tạo
- Giải sbt Kinh tế pháp luật 11 – Chân trời sáng tạo
- Giải sgk Lịch sử 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Lịch sử 11 – Chân trời sáng tạo
- Lý thuyết Lịch sử 11 - Chân trời sáng tạo
- Giải sbt Lịch sử 11 – Chân trời sáng tạo
- Giải sgk Địa lí 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Địa lí 11 – Chân trời sáng tạo
- Lý thuyết Địa lí 11 - Chân trời sáng tạo
- Giải sbt Địa lí 11 – Chân trời sáng tạo
- Giải sgk Hoạt động trải nghiệm 11 – Chân trời sáng tạo

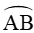 có độ dài đúng bằng R...
có độ dài đúng bằng R...