Nội dung bài viết

    Xem thêm

    Tìm cực trị của các hàm số sau: a) y = 2x^3 - 9x^2 + 12x - 5

    Lời giải Bài 1.7 trang 14 Toán 12 Tập 1 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12.

    1 6,043 08/06/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 12 Kết nối tri thức Bài 1: Tính đơn điệu và cực trị của hàm số

    Bài 1.7 trang 14 Toán 12 Tập 1: Tìm cực trị của các hàm số sau:

    a) y=2x3−9x2+12x−5;

    b) y=x4−4x2+2
    c) y=x2−2x+3x−1;
    d) y=4x−2x2.

    Lời giải:

    a) Tập xác định: D=R.

    y′=6x2−18x+12, y′=0⇔6x2−18x+12=0⇔[x=1x=2

    Bảng biến thiên:

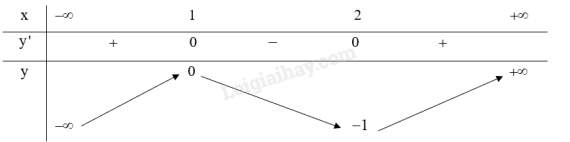
    Tài liệu VietJack

    Từ bảng biến thiên ta có:

    Hàm số y=2x3−9x2+12x−5 có điểm cực đại là (1;0).

    Hàm số y=2x3−9x2+12x−5 có điểm cực tiểu là (2;−1).

    b) Tập xác định của hàm số là R.

    Ta có: y′=4x3−8x,y′=0⇔4x3−8x=0⇔[x=0x=±2

    Bảng biến thiên:

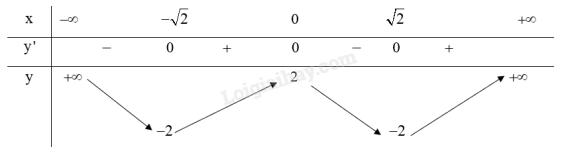
    Tài liệu VietJack

    Từ bảng biến thiên ta có:

    Hàm số y=x4−4x2+2 đạt cực đại tại x=0 và .

    Hàm số y=x4−4x2+2 đạt cực tiểu tại x=±2 và yCT=−2.

    c) Tập xác định: D=R∖{1}.

    Ta có: y′=(2x−2)(x−1)−(x2−2x+3)(x−1)2=x2−2x−1(x−1)2

    y′=0⇔[x=1−2x=1+2 (thỏa mãn)

    Lập bảng biến thiên của hàm số:

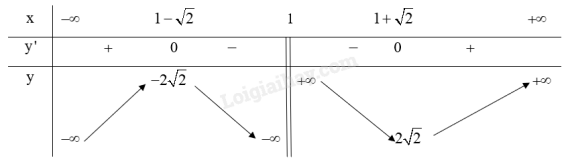
    Tài liệu VietJack

    Từ bảng biến thiên ta có:

    Hàm số y=x2−2x+3x−1 đạt cực đại tại x=1−2 và .

    Hàm số y=x2−2x+3x−1 đạt cực tiểu tại x=1+2 và yCT=22.

    d) y=4x−2x2

    Tập xác định: D=[0;2].

    Ta có: y′=(4x−2x2)′24x−2x2=−x+14x−2x2,y′=0⇔x=1(tm)

    Ta có bảng biến thiên của hàm số:

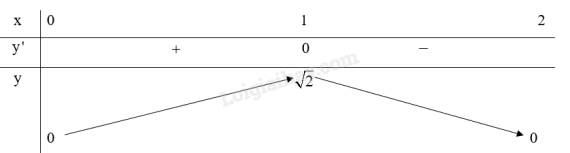
    Tài liệu VietJack

    Do đó, hàm số đạt cực đại tại x=1, , hàm số không có cực tiểu.

    Xem thêm các bài giải sách giáo khoa Toán 12 bộ sách Kết nối tri thức hay, chi tiết khác:

    HĐ 1 trang 6 Toán 12 Tập 1: Quan sát đồ thị của hàm số y=x2 (H.1.2) a) Hàm số đồng biến trên khoảng nào? b) Hàm số nghịch biến trên khoảng nào?

    Luyện tập 1 trang 6 Toán 12 Tập 1: Hình 1.5 là đồ thị của hàm số y=x3−3x2+2. Hãy tìm các khoảng đồng biến, khoảng nghịch biến của hàm số.

    HĐ 2 trang 6 Toán 12 Tập 1: a) Xét dấu đạo hàm của hàm số trên các khoảng (−∞;−1), (1;+∞). Nêu nhận xét về mối quan hệ giữa tính đồng biến, nghịch biến và dấu của đạo hàm...

    Luyện tập 2 trang 7 Toán 12 Tập 1: Tìm các khoảng đồng biến, khoảng nghịch biến của hàm số y=−x2+2x+3.

    HĐ 3 trang 7 Toán 12 Tập 1: Cho hàm số y=f(x)=x3−3x2+2x+1. a) Tính đạo hàm f′(x) và tìm các điểm x mà f′(x)=0....

    Luyện tập 3 trang 9 Toán 12 Tập 1: Tìm các khoảng đơn điệu của các hàm số sau: a) y=13x3+3x2+5x+2; b) y=−x2+5x−7x−2...

    Vận dụng 1 trang 9 Toán 12 Tập 1: Giải bài toán trong tình huống mở đầu bằng cách thực hiện lần lượt các yêu cầu sau...

    HĐ4 trang 9 Toán 12 Tập 1: Quan sát đồ thị của hàm số y=x3+3x2−4 (H.1.7). Xét dấu đạo hàm của hàm số đã cho và hoàn thành các bảng sau vào vở...

    Luyện tập 4 trang 10 Toán 12 Tập 1: Hình 1.9 là đồ thị của hàm số y=f(x). Hãy tìm các cực trị của hàm số...

    HĐ5 trang 10 Toán 12 Tập 1: Cho hàm số y=13x3−3x2+8x+1. a) Tính đạo hàm f′(x) và tìm các điểm mà tại đó đạo hàm f′(x) bằng 0...

    Câu hỏi trang 11 Toán 12 Tập 1: Giải thích vì sao nếu f’(x) không đổi dấu qua thì không phải là điểm cực trị của hàm số f(x)?

    Luyện tập 5 trang 12 Toán 12 Tập 1: Tìm cực trị của các hàm số sau: a) y=x4−3x2+1;  b) y=−x2+2x−1x+2...

    Vận dụng 2 trang 12 Toán 12 Tập 1: Một vật được phóng thẳng đứng lên trên từ độ cao 2m với vận tốc ban đầu là 24,5m/s...

    Bài 1.1 trang 13 Toán 12 Tập 1: Tìm các khoảng đồng biến, khoảng nghịch biến của các hàm số có đồ thị như sau: a) Đồ thị hàm số y=x3−32x2 (H.1.11);...

    Bài 1.2 trang 13 Toán 12 Tập 1: Xét sự đồng biến, nghịch biến của các hàm số sau: a) y=13x3−2x2+3x+1; b) y=−x3+2x2−5x+3...

    Bài 1.4 trang 13 Toán 12 Tập 1: Xét chiều biến thiên của các hàm số sau: a) y=4−x2; b) y=xx2+1...

    Bài 1.5 trang 13 Toán 12 Tập 1: Giả sử số dân của một thị trấn sau t năm kể từ năm 2000 được mô tả bởi hàm số N(t)=25t+10t+5,t≥0, trong đó N(t) được tính bằng nghìn người...

    Bài 1.6 trang 14 Toán 12 Tập 1: Đồ thị của đạo hàm bậc nhất y=f′(x) của hàm số f(x) được cho trong Hình 1.13: a) Hàm số f(x) đồng biến trên những khoảng nào? Giải thích...

    Bài 1.7 trang 14 Toán 12 Tập 1: Tìm cực trị của các hàm số sau: a) y=2x3−9x2+12x−5; b) y=x4−4x2+2...

    Bài 1.8 trang 14 Toán 12 Tập 1: Cho hàm số y=f(x)=|x|. a) Tính các giới hạn limx→0+⁡f(x)−f(0)x−0 và limx→0−⁡f(x)−f(0)x−0. Từ đó suy ra hàm số không có đạo hàm tại x=0...

    Bài 1.9 trang 14 Toán 12 Tập 1: Giả sử doanh số (tính bằng số sản phẩm) của một sản phẩm mới (trong vòng một số năm nhất định) tuân theo quy luật logistic được mô hình hóa...

    Xem thêm các bài giải sách giáo khoa Toán 12 bộ sách Kết nối tri thức hay, chi tiết khác:

    Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

    Bài 3: Đường tiệm cận của đồ thị hàm số

    Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số

    Bài 5: Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn

    Bài tập cuối chương 1 trang 42

    Tham khảo các loạt bài Toán 12 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 6,043 08/06/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: