Nội dung bài viết

    Xem thêm

    Lý thuyết Các phép toán với đa thức nhiều biến – Toán lớp 8 Chân trời sáng tạo

    Với lý thuyết Toán lớp 8 Bài 2: Các phép toán với đa thức nhiều biến chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sách Chân trời sáng tạo sẽ giúp học sinh nắm vững kiến thức trọng tâm để học tốt môn Toán 8.

    1 1,727 07/12/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Lý thuyết Toán 8 Bài 2: Các phép toán với đa thức nhiều biến - Chân trời sáng tạo

    Bài giảng Toán 8 Bài 2: Các phép toán với đa thức nhiều biến - Chân trời sáng tạo

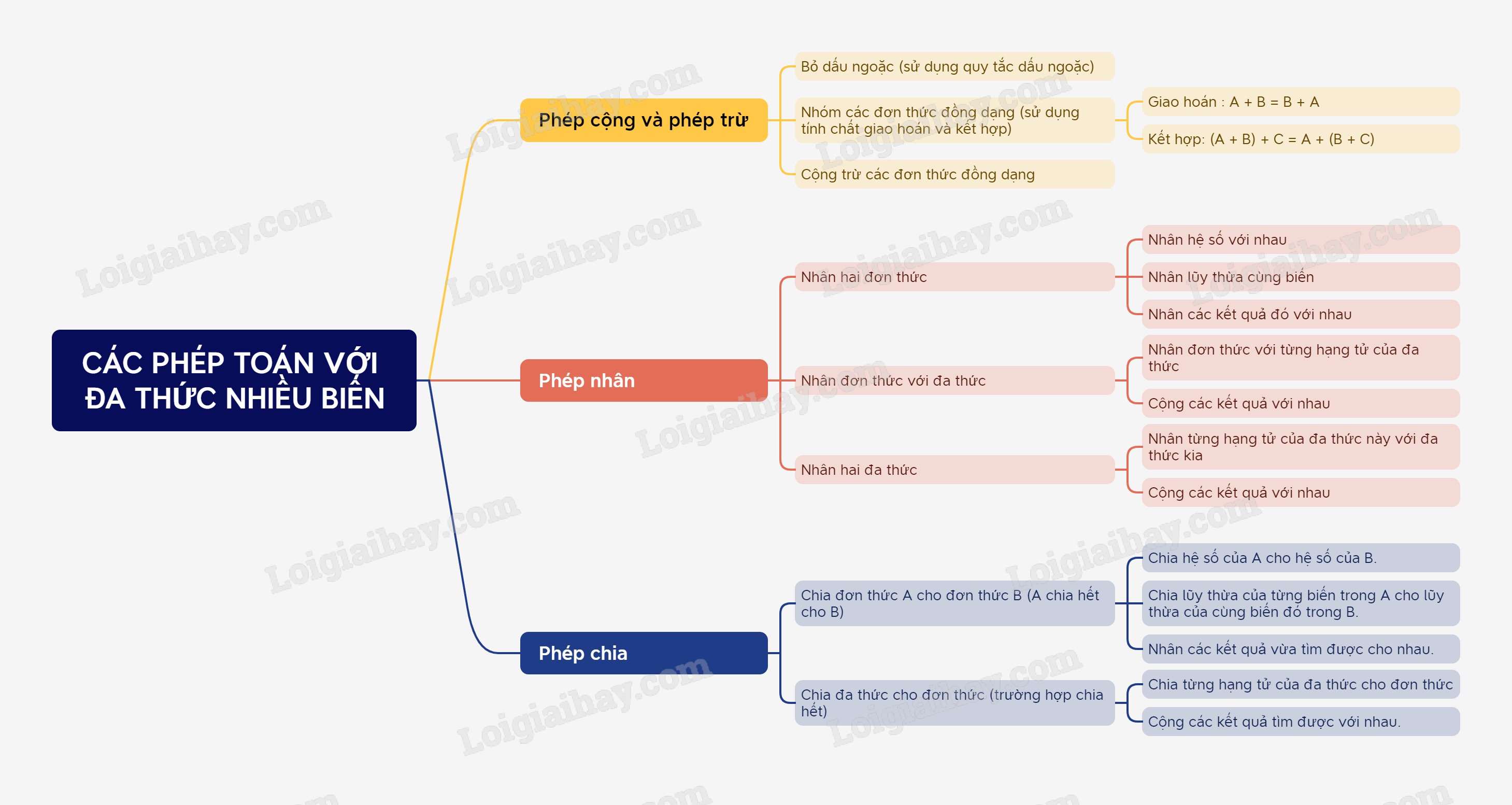
    A. Lý thuyết Các phép toán với đa thức nhiều biến

    1. Cộng và trừ hai đa thức

    Để cộng, trừ hai đa thức ta thực hiện các bước:

    - Bỏ dấu ngoặc (sử dụng quy tắc dấu ngoặc);

    - Nhóm các đơn thức đồng dạng (sử dụng tính chất giao hoán và kết hợp);

    - Cộng, trừ các đơn thức đồng dạng

    Ví dụ:

    Cho hai đa thức A=3x2−xyvà B=x2+2xy−y2

    A+B=(3x2−xy)+(x2+2xy−y2)=3x2−xy+x2+2xy−y2=(3x2+x2)+(−xy+2xy)−y2=4x2+xy−y2

    A−B=(3x2−xy)−(x2+2xy−y2)=3x2−xy−x2−2xy+y2=(3x2−x2)+(−xy−2xy)+y2=2x2−3xy+y2

    2. Nhân hai đơn thức

    Để nhân hai đơn thức, ta nhân các hệ số với nhau, nhân các lũy thừa cùng biến, rồi nhân các kết quả đó với nhau.

    Ví dụ: (−3x2y)(4xy)=[(−3.4)].(x2.x).(y.y)=−12.x3.y2

    3. Nhân đơn thức với đa thức

    Để nhân đơn thức với đa thức, ta nhân đơn thức đó với từng hạng tử của đa thức, rồi cộng các kết quả với nhau.

    Ví dụ:

    3x2y(2x2y−xy+3y2)=(3x2y).(2x2y)−(3x2y).(xy)+(3x2y).(3y2)=3.2.(x2.x2)(y.y)−3.(x2.x).(y.y)+3.3.x2.(y.y2)=6x4y2−3x3.y2+9x2y3

    4. Nhân hai đa thức

    Để nhân hai đa thức, ta nhân từng hạng tử của đa thức này với đa thức kia, rồi cộng các kết quả với nhau.

    Ví dụ:

    (xy+1)(xy−3)=(xy).(xy)+xy−3xy−3=x2y2−2xy−3

    5. Chia đơn thức cho đơn thức

    Muốn chia đơn thức A cho đơn thức B (với A chia hết cho B), ta làm như sau:

    - Chia hệ số của A cho hệ số của B.

    - Chia lũy thừa của từng biến trong A cho lũy thừa của cùng biến đó trong B.

    - Nhân các kết quả vừa tìm được cho nhau.

    Ví dụ:

    16x4y3:(−8x3y2)=(16:(−8)).(x4:x3).(y3:y2)=−2xy

    6. Chia đa thức cho đơn thức

    Muốn chia một đa thức cho một đơn thức (trường hợp chia hết), ta chia từng hạng tử của đa thức cho đơn thức đó, rồi cộng các kết quả tìm được với nhau.

    Ví dụ:

    (x2y+y2x):xy=x2y:xy+y2x:xy=x+y

    B. Bài tập Các phép toán với đa thức nhiều biến

    Đang cập nhật ...

    Xem thêm tóm tắt lý thuyết Toán lớp 8 sách Chân trời sáng tạo hay, chi tiết khác:

    Lý thuyết Bài 3: Hằng đẳng thức đáng nhớ

    Lý thuyết Bài 4: Phân tích đa thức thành nhân tử

    Lý thuyết Bài 5: Phân thức đại số

    Lý thuyết Bài 6: Cộng, trừ phân thức

    Lý thuyết Bài 7: Nhân, chia phân thức

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,727 07/12/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: