Trắc nghiệm Toán 10 Bài 5. Tích của một số với một vectơ có đáp án
Trắc nghiệm Toán 10 Bài 5. Tích của một số với một vectơ có đáp án
-
378 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
13/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: C
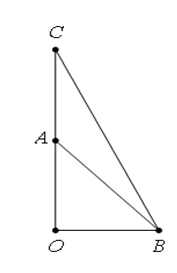
Gọi C là điểm đối xứng của O qua A ⇒OC=2a. Tam giác OBC vuông tại O có BC=√OB2+OC2=a√5.
Ta có : 2→OA−→OB=→OC−→OB=→BC, suy ra : |2→OA−→OB|=|→BC|=a√5.



Câu 2:
29/11/2024Cho tam giác OAB vuông cân tại O cạnh OA = a. Khẳng định nào sau đây sai:
 Xem đáp án
Xem đáp án
Đáp án đúng : C
*Lời giải
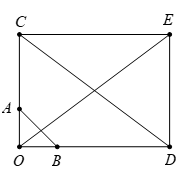
Dựa vào các đáp án, ta có nhận xét sau:
- Gọi C nằm trên tia đối của tia AO sao cho
OC=3 OA ⇒3 →OA=→OC.
Và D nằm trên tia đối của tia BO sao cho
OD=4 OB ⇒4 →OB=→OD.
Dựng hình chữ nhật OCED suy ra →OC+→OD=→OE (quy tắc hình bình hành).
Ta có: |3→OA+4→OB|=|→OC+→OD|=|→OE|=OE=CD=√OC2+OD2=5a.
Do đó, A đúng
- B đúng, vì |2 →OA|+|3 →OB|=2|→OA|+3|→OB|=2a+3a=5a.
- D đúng, vì |11 →OA|−|6 →OB|=11|→OA|−6|→OB|=11a−6a=5a.
*Phương pháp giải
- Ta sẽ dựng hình chữ nhật OCED với điều kiện: OC = 2OA và OD=4OB, suy ra vectơ vì cùng hướng.
- Áp dụng quy tắc hình bình hành cho hình chữ nhật với 2 cạnh OC và OD rồi thay thể lại về OA và OB để tính
- Đối chiếu với kết quả a,b,c,d xem kết quả nào đúng
*Một số lý thuyết nắm thêm tích vô hướng của một số với vectơ:
Ta quy ước k →a→a = →0→0 nếu →a→a = →0→0 hoặc k = 0.
Nhận xét: Vectơ k →a→a có độ dài bằng |k||→a→a| và cùng hướng với →a→a nếu k ≥ 0, ngược hướng với →a→a nếu →a→a ≠ →0→0 và k < 0.
Các tính chất của phép nhân vectơ với một số:
Với hai vectơ →a→a, →b→b và hai số thực k, t, ta luôn có :
+) k(t→a→a) = (kt) →a→a;
+) k (→a→a + →b→b) = k→a→a + k→b→b; k (→a→a – →b→b) = k→a→a – k→b→b;
+) (k + t) →a→a = k→a→a + t→a→a;
+) 1→a→a = →a→a; (–1) →a→a = –→a→a.
Nhận xét:
Điểm I là trung điểm của đoạn thẳng AB khi và chỉ khi −→IA+−→IB=→0→IA+→IB=→0.
Điểm G là trọng tâm của tam giác ABC khi và chỉ khi −−→GA+−−→GB+−−→GC=→0→GA+→GB+→GC=→0.
Xem thêm các bài viết liên quan hay, chi tiết:
Công thức phân tích vectơ (2024) chi tiết nhất
Trắc nghiệm Tổng và hiệu của hai vectơ có đáp án (Thông hiểu)
Câu 3:
16/07/2024Cho tam giác ABC có M là trung điểm của BC, I là trung điểm của AM. Khẳng định nào sau đây đúng ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
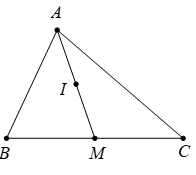
Vì M là trung điểm BC nên →IB+→IC=2→IM.
Mặt khác I là trung điểm AM nên →IA+→IM=→0.
Suy ra →IB+→IC+2→IA=2→IM+2→IA=2(→IM+→IA)=→0.
Câu 4:
23/07/2024Cho tam giác ABC có M là trung điểm của BC, I là trung điểm của AM. Khẳng định nào sau đây đúng ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
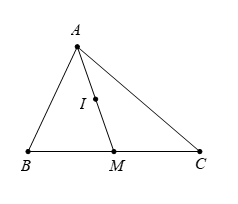
Vì M là trung điểm BC nên
→AB+→AC=2 →AM. (1)
Mặt khác I là trung điểm AM nên
2 →AI=→AM. (2)
Từ (1), (2) suy ra →AB+→AC=4 →AI⇔→AI=14(→AB+→AC).
Câu 5:
13/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: B
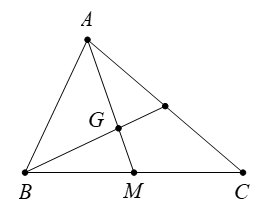
Vì G là trọng tâm của tam giác ABC
⇒→AG=23→AM.
Và M là trung điểm của BC
⇒→AB+→AC=2 →AM⇔→AM=12(→AB+→AC).
Do đó →AG=23.12(→AB+→AC)=13(→AB+→AC).
Câu 6:
14/07/2024Cho tứ giác ABCD. Trên cạnh AB, CD lấy lần lượt các điểm M, N sao cho 3 →AM=2 →AB và 3 →DN=2 →DC. Tính vectơ →MN theo hai vectơ →AD, →BC.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
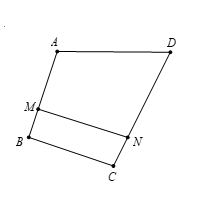
Ta có : →MN=→MA+→AD+→DN và →MN=→MB+→BC+→CN.
Suy ra 3 →MN=→MA+→AD+→DN+2(→MB+→BC+→CN)
=(→MA+2→MB)+→AD+2→BC+(→DN+2→CN).
Theo bài ra, ta có: →MA+2 →MB=→0 và →DN+2 →CN=→0. Thật vậy:
3 →AM=2 →AB⇔3→AM=2(→AM+→MB)
⇔3→AM=2→AM+2→MB
⇔→AM=2→MB
⇔2→MB−→AM=0
⇔2→MB+→MA=0
3 →DN=2 →DC⇔3 →DN=2(→DN+→NC)
⇔3 →DN=2→DN+2→NC
⇔→DN=2→NC
⇔→DN−2→NC=0
⇔→DN+2→CN=0
Vậy 3 →MN=→AD+2 →BC⇔→MN=13→AD+23→BC.
Câu 7:
22/07/2024Cho hình thang ABCD có đáy là AB và CD. Gọi M và N lần lượt là trung điểm của AD và BC. Khẳng định nào sau đây sai ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
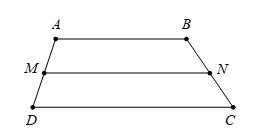
Vì M, N lần lượt là trung điểm của AD, BC
⇔{→MA+→MD=→0→BN+→CN=→0.
Dựa vào đáp án, ta có nhận xét sau:
- A đúng, vì →MD+→CN+→DC=(→MD+→DC)+→CN=→MC+→CN=→MN.
- B đúng, vì →AB−→MD+→BN=(→AB+→BN)−→MD=→AN−→AM=→MN. (vì M là trung điểm của AD nên →AM=→MD)
- C đúng, vì →MN=→MA+→AB+→BN và →MN=→MD+→DC+→CN.
Suy ra 2→MN=(→MA+→MD)+→AB+→DC+(→BN+→CN)=→0+→AB+→DC+→0=→AB+→DC
⇒→MN=12(→AB+→DC).
Vậy chỉ còn đáp án D.
Câu 8:
09/11/2024Cho hình bình hành ABCD có M là trung điểm của AB. Khẳng định nào sau đây đúng ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Lời giải
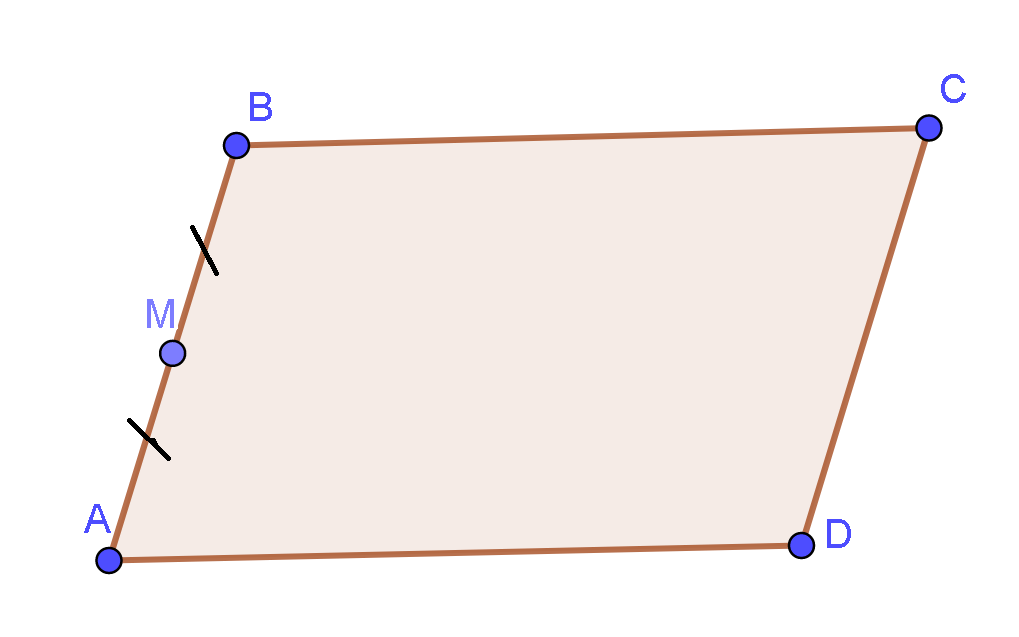
Xét các đáp án ta thấy cần phân tích vectơ →DM theo hai vectơ →DC và →BC
Vì ABCD là hình bình hành nên →DB=→DA+→DC.
Và M là trung điểm AB nên 2 →DM=→DA+→DB
⇔2 →DM=→DA+→DA+→DC
⇔2 →DM=2 →DA+→DC.
⇔2 →DM=− 2 →BC+→DC suy ra →DM=12→DC−→BC.
*Phương pháp giải:
Áp dụng quy tắc hình bình hành
Nếu ABCD là hình bình hành thì →AB+→AD=→AC.
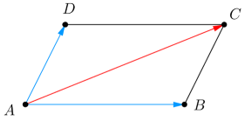
*Lý thuyết
- Quy tắc trung điểm: Với I là trung điểm của đoạn thẳng AB thì ta có:
→MA+→MB=2→MI ( M tùy ý )
→IA+→IB=→0
- Quy tắc trọng tâm: Với G là trọng tâm tam giác ABC thì ta có:
→MA+→MB+→MC=3→MG ( M tùy ý )
→GA+→GB+→GC=→0
- Quy tắc hình bình hành: Nếu ABCD là hình bình hành thì →AB+→AD=→AC.

B. Các công thức.
- Quy tắc trung điểm: I là trung điểm của AB
→IA+→IB=→0
→MA+→MB=2→MI ( M tùy ý )
- Quy tắc trọng tâm: G là trọng tâm tam giác ABC
→MA+→MB+→MC=3→MG ( M tùy ý )
→GA+→GB+→GC=→0
- Quy tắc hình hình hành: →AB+→AD=→AC ( ABCD là hình bình hành )
Xem thêm
Quy tắc trung điểm, trọng tâm, quy tắc hình bình hành vecto (2024) chi tiết nhất
TOP 40 câu Trắc nghiệm Hình bình hành (có đáp án - Toán 8
Câu 9:
12/07/2024Cho tam giác ABC điểm M thuộc cạnh AB sao cho 3 AM=AB và N là trung điểm của AC. Tính →MN theo →AB và →AC
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
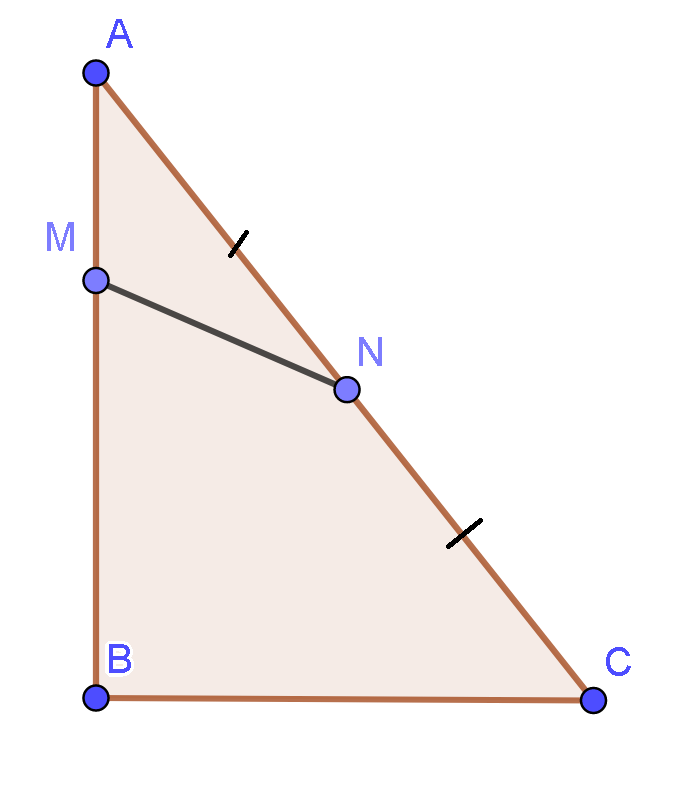
Vì N là trung điểm AC nên 2 →MN=→MA+→MC=→MA+→MA+→AC.
⇔2→MN=2 →MA+→AC
Do M là điểm thuộc cạnh AB và 3AM = AB nên →AB=3→AM=−3→MA
Do đó, 2→MN=2 →MA+→AC=−23→AB+→AC
Suy ra →MN=−13→AB+12→AC.
Câu 10:
12/07/2024Cho tam giác ABC. Hai điểm M, N chia cạnh BC theo ba phần bằng nhau BM=MN=NC. Tính →AM theo →AB và →AC
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
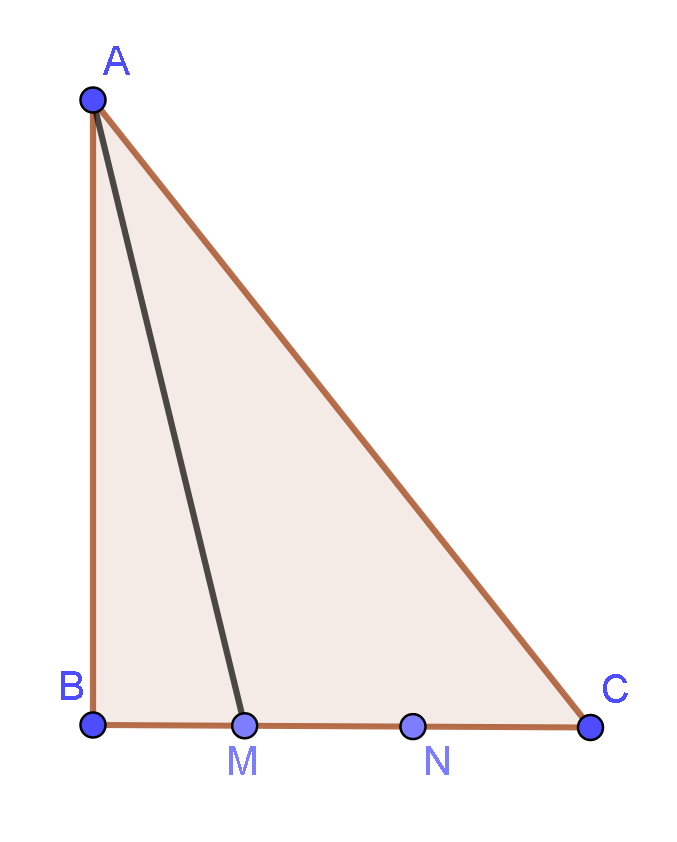
Theo giả thiết ta có: →BM=→MN=→NC=13→BC
Ta có: →AM=→AB+→BM=→AB+13→BC=→AB+13(→AC−→AB)=23→AB+13→AC.
Câu 11:
23/07/2024
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có : →AB=→AM+→MB=→AM−12→BC.
Câu 12:
12/07/2024Cho tam giác ABC, gọi M là trung điểm AB và N là một điểm trên cạnh AC sao cho NC=2NA. Gọi K là trung điểm của MN. Khi đó :
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
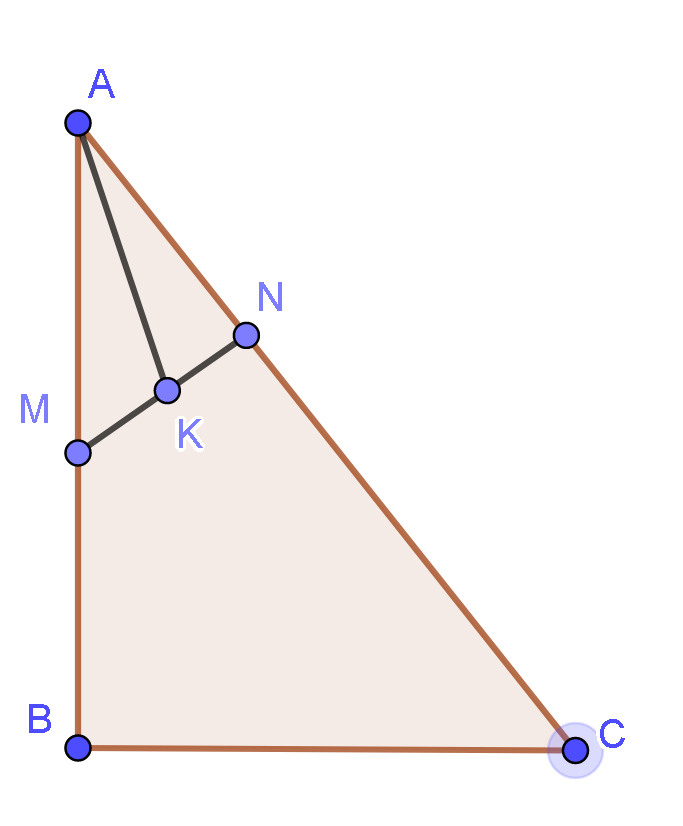
Vì K là trung điểm của MN nên ta có :
Ta có : →AK=12(→AM+→AN).
Mà M là trung điểm của AB và N là điểm thuộc cạnh AC sao cho NC = 2AN nên ta có : {→AM=12→AB→AN=13→AC
Do đó, →AK=12(12→AB+13→AC)=14→AB+16→AC
Câu 13:
30/10/2024Cho hình bình hành ABCD. Tính →AB theo →AC và →BD
 Xem đáp án
Xem đáp án
Đáp án đúng: A
*Lời giải
Vì ABCD là hình bình hành nên →CB+→AD=→0.
Ta có : {→AB=→AC+→CB→AB=→AD+→DB⇒2→AB=→AC+→DB+(→CB+→AD)=→AC+→DB
⇒→AB=12→AC+12→BD.
*Phương pháp giải
- vận dụng quy tắc hình bình hành và quy tắc cộng để biến đổi, tính toán
+ tách vectơ AB thành 2 vectơ nhỏ liên quan
+ cộng hai vế lại ta sẽ ra được kết quả cần tính
*Lý thuyết cần nắm và dạng bài toán về tích của một số với một vectơ:
a) Tính chất
Với hai vectơ bất kì →a→a, →b→b và hai số thực h, k, ta có:
+) k(→a→a + →b→b) = k→a→a + k→b→b; k(→a→a – →b→b) = k→a→a – k→b→b;
+) (h + k)→a→a = h→a→a + k→a→a;
+) h(k→a→a) = (hk)→a→a;
+) 1→a→a = →a→a; (–1)→a→a = –→a→a.
Nhận xét: k→a→a = →0→0 khi và chỉ khi k = 0 hoặc →a→a = →0→0.
b) Một số ứng dụng
Trung điểm của đoạn thẳng
Nếu I là trung điểm của đoạn thẳng AB thì −−→MA+−−→MB=2−→MI→MA+→MB=2→MI với điểm M bất kì.
Trọng tâm của tam giác
Nếu G là trọng tâm của tam giác ABC thì −−→MA+−−→MB+−−→MC=3−−→MG→MA+→MB+→MC=3→MG với điểm M bất kì.
Điều kiện để hai vectơ cùng phương. Điều kiện để ba điểm thẳng hàng
– Điều kiện cần và đủ để hai vectơ →a→a và →b→b (→b→b ≠ 0) cùng phương là có một số thực k để →a→a = k→b→b.
– Điều kiện cần và đủ để ba điểm phân biệt A, B, C thẳng hàng là có số thực k để −−→AB=k−−→AC→AB=k→AC.
Nhận xét: Trong mặt phẳng, cho hai vectơ →a→a và →b→b không cùng phương. Với mỗi vectơ →c→c có duy nhất cặp số (x; y) thoả mãn →c=x→a+y→b→c=x→a+y→b.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Tích của một số với một vectơ – Toán 10 Cánh diều
Giải Toán 10 Bài 5 (Cánh diều): Tích của một số với một vectơ
Trắc nghiệm Toán 10 Cánh diều Bài 5. Tích Của Một Số Với Một Vectơ có đáp án (Phần 2)
Câu 14:
12/07/2024Cho tam giác ABC và đặt →a=→BC, →b=→AC. Cặp vectơ nào sau đây cùng phương?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Dễ thấy −10 →a−2→b=− 2 (5→a+→b) ⇒ hai vectơ 5→a+→b, −10→a−2→b cùng phương
Câu 15:
23/07/2024Cho tam giác ABC và điểm M thỏa mãn →MA=→MB+→MC. Khẳng định nào sau đây đúng ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Gọi I, G lần lượt là trung điểm BC và trọng tâm tam giác ABC
Vì I là trung điểm BC nên →MB+→MC=2 →MI.
Theo bài ra, ta có →MA=→MB+→MC suy ra →MA=2→MI ⇔A, M, I thẳng hàng
Mặt khác G là trọng tâm của tam giác ABC⇒ G∈AI.⇒A, M, G thẳng hàng.
Có thể bạn quan tâm
- Trắc nghiệm Toán 10 Bài 5. Tích của một số với một vectơ có đáp án (377 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 5. Tích Của Một Số Với Một Vectơ có đáp án (Phần 2) (667 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Toán 10 Bài 2. Giải tam giác. Tính diện tích tam giác có đáp án (1165 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 2. Giải Tam Giác có đáp án (Phần 2) (732 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 1. Giá trị lượng giác của một góc từ 0° đến 180°. Định lí côsin và định lí sin trong tam giác có đáp án (phần 2) (661 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 6. Tích vô hướng của hai vectơ có đáp án (Phần 2) (617 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 4. Tổng và hiệu của hai vectơ có đáp án (Phần 2) (595 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 3. Vectơ có đáp án (Phần 2) (590 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài tập cuối chương 4 có đáp án (Phần 2) (585 lượt thi)
- Trắc nghiệm Toán 10 Bài 1. Giá trị lượng giác của một góc từ 0 độ đến 180 độ . Định lý cosin và sin trong tam giác có đáp án (468 lượt thi)
- Trắc nghiệm Toán 10 Bài 3. Khái niệm vectơ có đáp án (406 lượt thi)
- Trắc nghiệm Toán 10 Bài 4. Tổng và hiệu hai vectơ có đáp án (390 lượt thi)
