Trắc nghiệm Toán 10 Cánh diều Bài 5. Tích Của Một Số Với Một Vectơ có đáp án (Phần 2)
Trắc nghiệm Toán 10 Cánh diều Bài 5. Tích Của Một Số Với Một Vectơ có đáp án (Phần 2) (Nhận biết)
-
532 lượt thi
-
7 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
12/07/2024Cho tam giác ABC có G là trọng tâm và I là trung điểm của BC. Đẳng thức nào sau đây là đúng?
Xem đáp án
Đáp án đúng là: C
Vì I là trung điểm của BC suy ra
Ta có .
Câu 2:
22/07/2024 Xem đáp án
Đáp án đúng là: C
Câu 3:
22/07/2024Cho tam giác ABC vuông tại A, M là trung điểm BC. Khẳng định nào sau đây đúng?
Xem đáp án
Đáp án đúng là: C
Vì M là trung điểm của BC nên . Vậy đáp án C đúng.
Câu 4:
28/11/2024Cho tam giác ABC. Gọi M và N lần lượt là trung điểm của AB và AC. Khẳng định nào sau đây sai?
Xem đáp án
Đáp án đúng là: C
Lời giải
+) Do M là trung điểm của AB nên AB = 2AM, hơn nữa hai vectơ cùng hướng nên ta có . Vậy đáp án A đúng.
+) Tương tự, N là trung điểm của AC nên ta cũng có hay . Vậy đáp án B, D đúng.
+) Vì M, N lần lượt là trung điểm của AB, AC.
Suy ra MN là đường trung bình của tam giác ABC Þ MN // BC và
Do đó, hai vectơ cùng phương.
Mà là hai vectơ cùng hướng nên Vậy đáp án C sai.
*Phương pháp giải:
Sử dụng 2 vecto cung phương
*Lý thuyết:
Định nghĩa:
– Hai vectơ cùng phương: Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
Ví dụ:
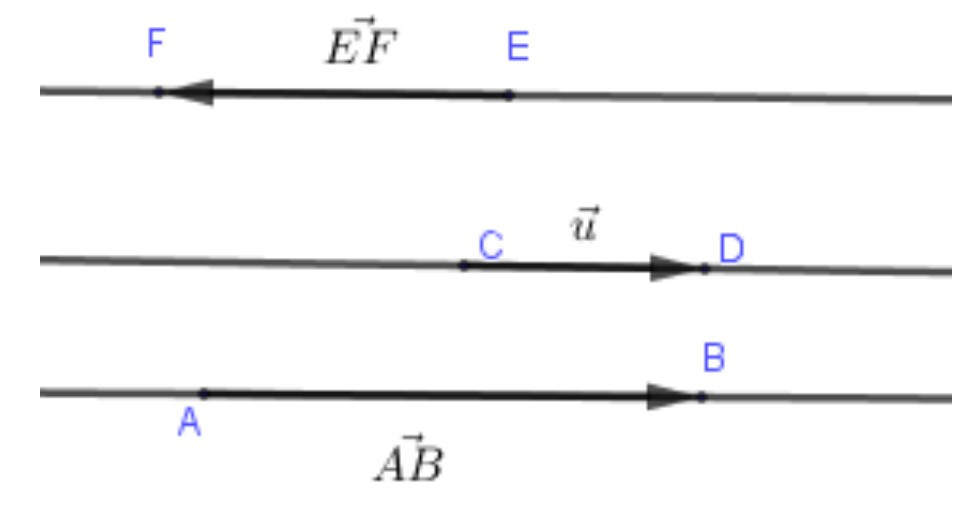
Trên hình vẽ các vectơ , , cùng phương với nhau.
Nhận xét: Hai vectơ cùng phương có thể cùng hướng hoặc ngược hướng.
Ví dụ:
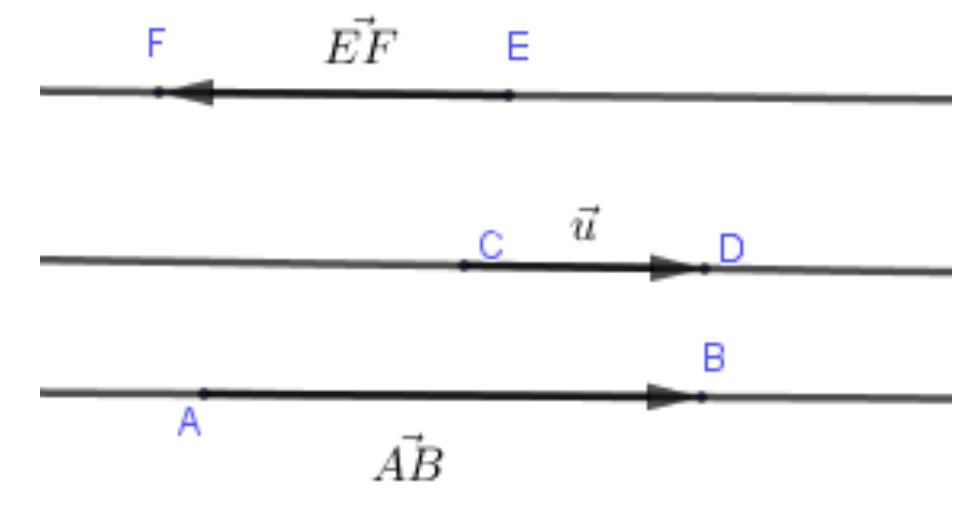
Hai vectơ và cùng phương và có cùng hướng đi từ trái sang phải. Ta nói hai vectơ và cùng hướng. Hai vectơ và cùng phương nhưng ngược hướng nhau. Ta nói hai vectơ và là hai vectơ ngược hướng.
Ví dụ: Cho hình bình hành ABCD. Liệt kê các cặp vectơ cùng hướng và ngược hướng trong hình bình hành ABCD.
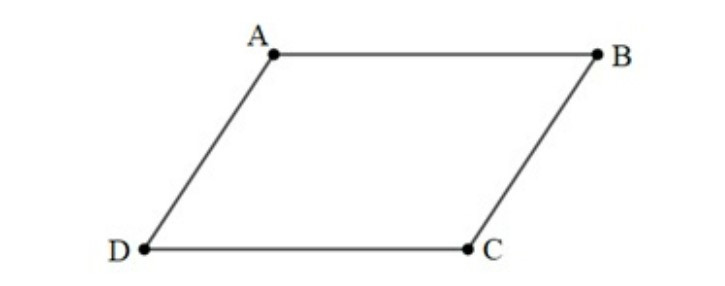
Hướng dẫn giải:
Do ABCD là hình bình hành nên ta có: AB // DC và AD // BC.
Các cặp vectơ cùng hướng: và , và , và , và .
Các cặp vectơ ngược hướng: và , và , và , và .
Xem thêm
Câu 5:
20/07/2024Cho tam giác ABC có G là trọng tâm. Mệnh đề nào sau đây đúng?
Xem đáp án
Đáp án đúng là: B
Gọi E là trung điểm của AC (1)
Mà G là trọng tâm của tam giác ABC nên ta có: (2)
Từ (1), (2) suy ra:
