Cho tam giác OAB vuông cân tại O cạnh OA = a. Khẳng định nào sau đây sai:

Đáp án đúng : C

*Lời giải

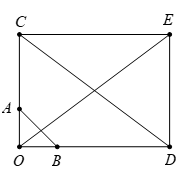
Dựa vào các đáp án, ta có nhận xét sau:

- Gọi C nằm trên tia đối của tia AO sao cho

$OC=3OA$ $\Rightarrow 3\overrightarrow{OA}=\overrightarrow{OC}.$

Và D nằm trên tia đối của tia BO sao cho

$OD=4OB$  $\Rightarrow 4\overrightarrow{OB}=\overrightarrow{OD}.$

Dựng hình chữ nhật OCED suy ra $\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{OE}$ (quy tắc hình bình hành).

Ta có: $\left|3\overrightarrow{OA}+4\overrightarrow{OB}\right|=\left|\overrightarrow{OC}+\overrightarrow{OD}\right|=\left|\overrightarrow{OE}\right|=OE=CD=\sqrt{O{C}^2+O{D}^2}=5a.$ 

Do đó, A đúng

- B đúng, vì $\left|2\overrightarrow{OA}\right|+\left|3\overrightarrow{OB}\right|=2\left|\overrightarrow{OA}\right|+3\left|\overrightarrow{OB}\right|=2a+3a=5a.$

- D đúng, vì $\left|11\overrightarrow{OA}\right|-\left|6\overrightarrow{OB}\right|=11\left|\overrightarrow{OA}\right|-6\left|\overrightarrow{OB}\right|=11a-6a=5a.$

*Phương pháp giải 

- Ta sẽ dựng hình chữ nhật OCED với điều kiện: OC = 2OA và OD=4OB, suy ra vectơ vì cùng hướng. 

- Áp dụng quy tắc hình bình hành cho hình chữ nhật với 2 cạnh OC và OD rồi thay thể lại về OA và OB để tính

- Đối chiếu với kết quả a,b,c,d xem kết quả nào đúng

*Một số lý thuyết nắm thêm tích vô hướng của một số với vectơ:

Ta quy ước k $\overrightarrow{a}$ = $\overrightarrow{0}$ nếu $\overrightarrow{a}$ = $\overrightarrow{0}$ hoặc k = 0.

 

Nhận xét: Vectơ k $\overrightarrow{a}$ có độ dài bằng |k||$\overrightarrow{a}$| và cùng hướng với $\overrightarrow{a}$ nếu k ≥ 0, ngược hướng với $\overrightarrow{a}$ nếu $\overrightarrow{a}$ ≠ $\overrightarrow{0}$ và k < 0.

Các tính chất của phép nhân vectơ với một số:

Với hai vectơ $\overrightarrow{a}$, $\overrightarrow{b}$ và hai số thực k, t, ta luôn có :

+) k(t$\overrightarrow{a}$) = (kt) $\overrightarrow{a}$;

+) k ($\overrightarrow{a}$ + $\overrightarrow{b}$) = k$\overrightarrow{a}$ + k$\overrightarrow{b}$; k ($\overrightarrow{a}$ – $\overrightarrow{b}$) = k$\overrightarrow{a}$ – k$\overrightarrow{b}$;

+) (k + t) $\overrightarrow{a}$ = k$\overrightarrow{a}$ + t$\overrightarrow{a}$;

+) 1$\overrightarrow{a}$ = $\overrightarrow{a}$; (–1) $\overrightarrow{a}$ = –$\overrightarrow{a}$.

Nhận xét:

Điểm I là trung điểm của đoạn thẳng AB khi và chỉ khi $\overrightarrow{IA}+\overrightarrow{IB}=\overrightarrow{0}$.

 

Điểm G là trọng tâm của tam giác ABC khi và chỉ khi $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$.

Xem thêm các bài viết liên quan hay, chi tiết: 

Công thức phân tích vectơ (2024) chi tiết nhất

Trắc nghiệm Tổng và hiệu của hai vectơ có đáp án (Thông hiểu)