25 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 8 Bài 4: Phương trình tích

Câu 1:

22/07/2024

Các nghiệm của phương trình (2 - 6x)(-x² – 4) = 0 là

A. x = 3

B. x =-

\frac{1}{3}

C. x = -3

D.x =

\frac{1}{3}

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

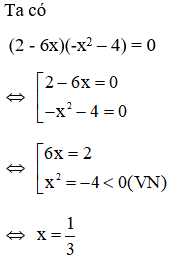
Phương trình có ngiệm duy nhất x = $\frac{1}{3}$

Câu 2:

21/07/2024

Tổng các nghiệm của phương trình

(x² – 4)(x + 6)(x – 8) = 0 là

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Đáp án: B

Giải thích:

Lời giải

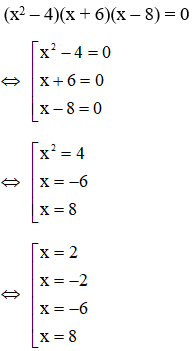
Tổng các nghiệm của phương trình

là 2 + (-2) + (-6) + 8 = 2

Câu 3:

21/07/2024

Phương trình (x² – 1)(x – 2)(x – 3) = 0

có số nghiệm là

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

Ta có (x² – 1)(x – 2)(x – 3) = 0

$\Leftrightarrow [\begin{array}{l} x^{2} - 1 = 0 \\ x - 2 = 0 \\ x - 3 = 0 \end{array}$

$\Leftrightarrow [\begin{array}{l} x = \pm 1 \\ x = 2 \\ x = 3 \end{array}$

Vậy phương trình có

bốn nghiệm x = -1; x = 1, x = 2, x = 3

Câu 4:

17/07/2024

Tìm m để phương trình (2m – 5)x – 2m² – 7 = 0

nhận x = -3 làm nghiệm

A. m = 1 hoặc m = 4

B. m = -1 hoặc m = -4

C. m = -1 hoặc m = 4

D. m = 1 hoặc m = -4

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

Thay x = -3 vào phương trình

(2m – 5)x – 2m² – 7 = 0 ta được

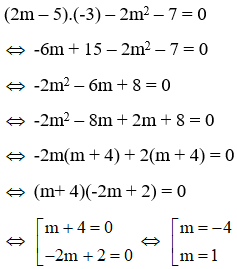
Vậy m = 1 hoặc m = -4

thì phương trình có nghiệm x = -3

Câu 5:

19/07/2024

Tập nghiệm của phương trình (2x + 1)(2 - 3x) = 0 là

Tập nghiệm của phương trình (2x + 1)(2 - 3x) = 0 là (ảnh 1)

Xem đáp án

Đáp án: C

Giải thích:

Lời giải

Ta có (2x + 1)(2 - 3x) = 0

$\Leftrightarrow [\begin{array}{l} 2 x + 1 = 0 \\ 2 - 3 x = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = - \frac{1}{2} \\ x = \frac{2}{3} \end{array}$

Vậy tập nghiệm của phương trình đã cho là

S = $\{- \frac{1}{2}; \frac{2}{3}\}$ .

Câu 6:

15/07/2024

Tổng các nghiệm của phương trình

(x² + 4)(x + 6)(x² – 16) = 0 là

A. 16

B. 6

C. -10

D. -6

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

Ta có (x² + 4)(x + 6)(x² – 16) = 0

$\Leftrightarrow [\begin{array}{l} x^{2} + 4 = 0 \\ x + 6 = 0 \\ x^{2} - 16 = 0 \end{array}$

$\Leftrightarrow [\begin{array}{l} x^{2} = - 4 (V N) \\ x = - 6 \\ x^{2} = 16 \end{array}$

$\Leftrightarrow [\begin{array}{l} x^{2} = - 4 (V N) \\ x = - 6 \\ x = \pm 4 \end{array}$

Tổng các nghiệm của phương trình

là: -6 + (-4) + 4 = -6

Câu 7:

19/07/2024

Số nghiệm của phương trình

$2 x^{2} + 3 x + 4 = x^{2} + x + 4$ là

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Đáp án: C

Giải thích:

Lời giải

Câu 8:

22/07/2024

Tập nghiệm của phương trình

(5x² – 2x + 10)² = (3x² +10x – 8)²là:

A. S = {

\frac{1}{2}

; 3}

B. S = {

\frac{1}{2}

; -3}

C. S = {-

\frac{1}{2}

; 3}

D. S = {-

\frac{1}{2}

; -3}

Xem đáp án

Đáp án: C

Giải thích:

Lời giải

(5x² – 2x + 10)² = (3x² +10x – 8)²

$\Leftrightarrow$ (5x² – 2x + 10)² - (3x² +10x – 8)² = 0

$\Leftrightarrow$ (5x² – 2x + 10 + 3x² +10x – 8)(5x² – 2x + 10 – 3x² – 10x + 8) = 0

$\Leftrightarrow$ (8x² + 8x + 2)(2x² – 12x + 18) = 0

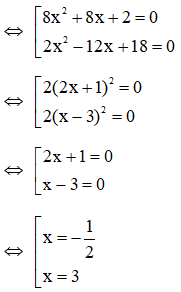
Vậy phương trình có tập nghiệm: S = {- $\frac{1}{2}$ ; 3}

Câu 9:

15/07/2024

Tìm m để phương trình

(2m – 5)x – 2m²+ 8 = 43 có nghiệm x = -7

A. m = 0 hoặc m = 7

B. m = 1 hoặc m = -7

C. m = 0 hoặc m = -7

D. m = -7

Xem đáp án

Đáp án: C

Giải thích:

Lời giải

Thay x = -7 vào phương trình (2m – 5)x – 2m²+ 8 = 43 ta được:

(2m – 5)(-7) – 2m² + 8 = 43

$\Leftrightarrow$ -14m + 35 – 2m² – 35 = 0

$\Leftrightarrow$ 2m² + 14m = 0

$\Leftrightarrow$ 2m(m + 7) = 0

$\Leftrightarrow [\begin{array}{l} m = 0 \\ m + 7 = 0 \end{array}$

$\Leftrightarrow [\begin{array}{l} m = 0 \\ m = - 7 \end{array}$

Vậy m = 0 hoặc m = -7

thì phương trình có nghiệm x = -7

Câu 10:

21/07/2024

Số nghiệm của phương trình

(5x² – 2x + 10)³ = (3x² +10x – 6)³là

A. 1

B. 2

C. 3

D. 0

Xem đáp án

Đáp án: B

Giải thích:

Lời giải

(5x² – 2x + 10)³ = (3x² +10x – 6)³

$\Leftrightarrow$ 5x² – 2x + 10 = 3x² +10x – 6

$\Leftrightarrow$ 5x² – 3x² – 2x – 10x + 10 + 6 = 0

$\Leftrightarrow$ 2x² – 12x + 16 = 0

$\Leftrightarrow$ x² – 6x + 8 = 0

$\Leftrightarrow$ x² – 4x – 2x + 8 = 0

$\Leftrightarrow$ x(x – 4) – 2(x – 4) = 0

$\Leftrightarrow$ (x – 2)(x – 4) = 0

$\Leftrightarrow$ $[\begin{array}{l} x - 2 = 0 \\ x - 4 = 0 \end{array}$

$\Leftrightarrow$ $[\begin{array}{l} x = 2 \\ x = 4 \end{array}$

Vậy phương trình có 2 nghiệm

Câu 11:

20/07/2024

Chọn khẳng định đúng.

A. Phương trình 8x(3x – 5) = 6(3x – 5) có hai nghiệm trái dấu

B. Phương trình 8x(3x – 5) = 6(3x – 5) có hai nghiệm dương

C. Phương trình 8x(3x – 5) = 6(3x – 5) có hai nghiệm cùng âm

D. Phương trình 8x(3x – 5) = 6(3x – 5) có một nghiệm duy nhất

Xem đáp án

Đáp án: B

Giải thích:

Lời giải

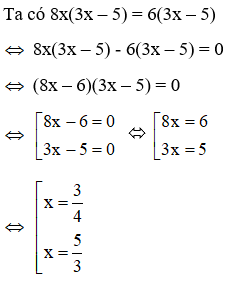
Vậy phương trình đã cho có hai nghiệm

cùng dương $x = \frac{3}{4}; x = \frac{5}{3}$

Câu 12:

23/07/2024

Tập nghiệm của phương trình

(x² – x – 1)(x² – x + 1) = 3 là

A. S = {-1; -2}

B. S = {1; 2}

C. S = {1; -2}

D. S = {-1; 2}

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

Đặt x² - x = y, ta có

(y – 1)(y + 1)= 3

$\Leftrightarrow$ y² – 1 = 3

$\Leftrightarrow$ y² = 4 y = ±2

Với y = 2 ta có: x² – x = 2

$\Leftrightarrow$ x² – x – 2 = 0

$\Leftrightarrow$ x² – 2x + x – 2 = 0

$\Leftrightarrow$ x(x – 2) + (x – 2) = 0

$\Leftrightarrow$ (x – 2)(x + 1) = 0

$\Leftrightarrow$ $[\begin{array}{l} x - 2 = 0 \\ x + 1 = 0 \end{array}$

$\Leftrightarrow$ $[\begin{array}{l} x = 2 \\ x = - 1 \end{array}$

Với y = -2 ta có: x² – x = -2

$\Leftrightarrow (x^{2} - 2. \frac{1}{2} . x + \frac{1}{4}) + \frac{7}{4} = 0$

$\Leftrightarrow {(x - \frac{1}{2})}^{2} + \frac{7}{4} = 0$ vô nghiệm

vì ${(x - \frac{1}{2})}^{2} + \frac{7}{4} > 0$ với mọi x $\in$ R

Vậy tập nghiệm của phương trình là S = {-1; 2}

Câu 13:

17/07/2024

Biết rằng phương trình (x² – 1)² = 4x + 1

có nghiệm lớn nhất là x₀. Chọn khẳng định đúng

A. x₀ = 3

B. x₀ < 2

C. x₀ > 1

D. x₀ < 0

Xem đáp án

Đáp án: C

Giải thích:

Lời giải

Ta có (x² – 1)² = 4x + 1

$\Leftrightarrow$ x⁴ – 2x² + 1 = 4x + 1

$\Leftrightarrow$ x⁴ – 2x² + 1 + 4x² = 4x² + 4x + 1

(Cộng 4x² vào hai vế)

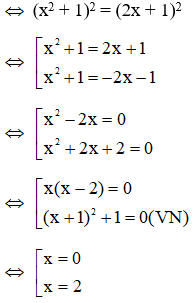
Vậy S = {0; 2}, nghiệm lớn nhất là x₀ = 2 > 1

Câu 14:

20/07/2024

Cho phương trình 5 – 6(2x – 3) = x(3 – 2x) + 5.

Chọn khẳng định đúng

A. Phương trình có hai nghiệm trái dấu

B. Phương trình có hai nghiệm nguyên

C. Phương trình có hai nghiệm cùng dương

D. Phương trình có một nghiệm duy nhất

Xem đáp án

Đáp án: C

Giải thích:

Lời giải

Ta có 5 – 6(2x – 3) = x(3 – 2x) + 5

5 – 5 = x(3 – 2x) + 6(2x – 3)

0 = -x(2x – 3) + 6(2x – 3)

(2x – 3)(-x + 6) = 0

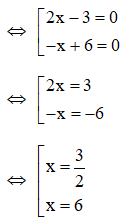
Vậy phương trình đã cho có hai nghiệm

cùng dương x = ; x = 6

Đáp án cần chọn là: C

Câu 15:

15/07/2024

Biết rằng phương trình (4x² – 1)² = 8x + 1

có nghiệm lớn nhất là x₀. Chọn khẳng định đúng

A. x₀ = 3

B. x₀ < 2

C. x₀ > 1

D. x₀ < 0

Xem đáp án

Đáp án: B

Giải thích:

Lời giải

Cộng 16x² vào hai vế của phương trình đã cho ta được

(4x² – 1)² +16x² = 16x² + 8x + 1

$\Leftrightarrow$ 16x⁴ – 8x² + 1 + 16x² = 16x² + 8x + 1

$\Leftrightarrow$ (4x² + 1)² = (4x + 1)²

$\Leftrightarrow$ (4x² + 1 + 4x + 1)(4x² + 1 – 4x – 1) = 0

$\Leftrightarrow$ (4x² + 4x + 2)(4x² – 4x) = 0

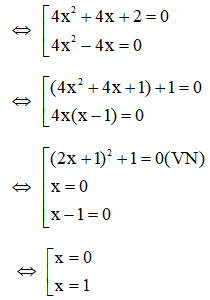
Vậy S = {0; 1}, nghiệm lớn nhất là x₀ = 1 < 2

Câu 16:

23/07/2024

Tích các nghiệm của phương trình

x³ + 4x² + x – 6 = 0 là

A. 1

B. 2

C. -6

D. 6

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

Ta có

x³ + 4x² + x – 6 = 0

$\Leftrightarrow$ x³ – x² + 5x² – 5x + 6x – 6 = 0

$\Leftrightarrow$ x²(x – 1) + 5x(x – 1) + 6(x – 1) = 0

$\Leftrightarrow$ (x – 1)(x² + 5x + 6) = 0

$\Leftrightarrow$ (x – 1)(x² + 2x + 3x + 6) = 0

$\Leftrightarrow$ (x – 1)[x(x + 2) + 3(x + 2)] = 0

$\Leftrightarrow$ (x – 1)(x + 2)(x + 3)= 0

$\Leftrightarrow [\begin{array}{l} x - 1 = 0 \\ x + 2 = 0 \\ x + 3 = 0 \end{array}$

$\Leftrightarrow [\begin{array}{l} x = 1 \\ x = - 2 \\ x = - 3 \end{array}$

Vậy S = {1; -2; -3} nên tích

các nghiệm là 1.(-2).(-3) = 6

Câu 17:

19/07/2024

Cho phương trình (1): x(x² – 4x + 5) = 0

và phương trình (2): (x² – 1)(x² + 4x + 5) = 0.

Chọn khẳng định đúng

A. Phương trình (1) có một nghiệm, phương trình (2) có hai nghiệm

B. Phương trình (1) có hai nghiệm, phương trình (2) có một nghiệm

C. Hai phương trình đều có hai nghiệm

D. Hai phương trình đều vô nghiệm

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

Xét phương trình (1): x(x² – 4x + 5) = 0

$\Leftrightarrow [\begin{array}{l} x = 0 \\ x^{2} - 4 x + 5 = 0 \end{array}$

$\Leftrightarrow [\begin{array}{l} x = 0 \\ {(x - 2)}^{2} + 1 = 0 (V N) \end{array}$

Vậy phương trình (1) có một nghiệm duy nhất x = 0.

Xét phương trình (2):

(x² – 1)(x² + 4x + 5) = 0

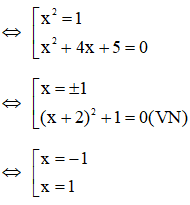
Vậy phương trình (2) có hai nghiệm x = -1; x = 1

Câu 18:

15/07/2024

Tích các nghiệm của phương trình

x³ – 3x² – x + 3 = 0 là

A. -3

B. 3

C. -6

D. 6

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

Ta có x³ – 3x² – x + 3 = 0

$\Leftrightarrow$ (x³ – 3x²) – (x – 3) = 0

$\Leftrightarrow$ x²(x – 3) – (x – 3)= 0

$\Leftrightarrow$ (x – 3)(x² – 1) = 0

$\Leftrightarrow$ (x – 3)(x – 1)(x + 1) = 0

$\Leftrightarrow [\begin{array}{l} x - 3 = 0 \\ x - 1 = 0 \\ x + 1 = 0 \end{array}$

$\Leftrightarrow [\begin{array}{l} x = 3 \\ x = 1 \\ x = - 1 \end{array}$

Vậy S = {1; -1; 3}

nên tích các nghiệm là 1.(-1).3 = -3

Câu 19:

23/07/2024

Cho phương trình x⁴ – 8x² + 16 = 0. Chọn khẳng định đúng

A. Phương trình có hai nghiệm đối nhau

B. Phương trình vô nghiệm

C. Phương trình có một nghiệm duy nhất

D. Phương trình có 4 nghiệm phân biệt

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

Ta có x⁴ – 8x² + 16 = 0

$\Leftrightarrow$ (x²)² – 2.4.x² + 4² = 0

$\Leftrightarrow$ (x² – 4)² = 0

$\Leftrightarrow$ x² – 4 = 0

$\Leftrightarrow$ (x – 2)(x + 2) = 0

$\Leftrightarrow [\begin{array}{l} x - 2 = 0 \\ x + 2 = 0 \end{array}$

$\Leftrightarrow [\begin{array}{l} x = 2 \\ x = - 2 \end{array}$

Vậy phương trình có hai nghiệm phân biệt đối nhau

Câu 20:

23/07/2024

Nghiệm lớn nhất của phương trình

(x² – 1)(2x – 1) = (x² – 1)(x + 3) là

A. 2

B. 1

C. -1

D. 4

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

Ta có (x² – 1)(2x – 1) = (x² – 1)(x + 3)

$\Leftrightarrow$ (x² – 1)(2x – 1) – (x² – 1)(x + 3) = 0

$\Leftrightarrow$ (x² – 1)(2x – 1 – x – 3) = 0

$\Leftrightarrow$ (x² – 1)(x – 4) = 0

$\Leftrightarrow [\begin{array}{l} x^{2} - 1 = 0 \\ x - 4 = 0 \end{array}$

$\Leftrightarrow [\begin{array}{l} x^{2} = 1 \\ x = 4 \end{array}$

$\Leftrightarrow [\begin{array}{l} x = \pm 1 \\ x = 4 \end{array}$

Vậy tập nghiệm của phương trình S = {-1; 1; 4}

Nghiệm lớn nhất của phương trình là x = 4

Câu 21:

22/07/2024

Các nghiệm của phương trình (2 + 6x)(-x² – 4) = 0 là

A. x = 2

B. x = -2

C. x =-

\frac{1}{2}

; x = 2

D. x =-

\frac{1}{3}

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

Ta có (2 + 6x)(-x² – 4) = 0

$\Leftrightarrow [\begin{array}{l} 2 + 6 x = 0 \\ - x^{2} - 4 = 0 \end{array}$

$\Leftrightarrow [\begin{array}{l} 6 x = - 2 \\ - x^{2} = 4 \end{array}$

$\Leftrightarrow [\begin{array}{l} x = - \frac{1}{3} \\ x^{2} = - 4 (V N) \end{array}$

Phương trình có ngiệm duy nhất x =- $\frac{1}{3}$

Câu 22:

15/07/2024

Tập nghiệm của phương trình

(x² + x)(x² + x + 1) = 6 là

A. S = {-1; -2}

B. S = {1; 2}

C. S = {1; -2}

D. S = {-1; 2}

Xem đáp án

Đáp án: C

Giải thích:

Lời giải

Đặt x² + x = y, ta có

$\Leftrightarrow$ y(y + 1) = 6 y² + y – 6 = 02²

$\Leftrightarrow$ y² – 2y + 3y – 6 = 0

$\Leftrightarrow$ y(y – 2) + 3(y – 2) = 0

$\Leftrightarrow$ (y – 2)(y + 3) = 0

$\Leftrightarrow$ $[\begin{array}{l} y = - 3 \\ y = 2 \end{array}$

+ Với y = –3, ta có x² + x + 3 = 0, vô nghiệm vì

x² + x + 3 = ${(x + \frac{1}{2})}^{2} + \frac{11}{4} > 0$

+ Với y = 2, ta có x² + x – 2 = 0

$\Leftrightarrow$ x² + 2x – x – 2 = 0

$\Leftrightarrow$ x(x + 2) – (x + 2) = 0

$\Leftrightarrow$ (x + 2)(x – 1) = 0

$\Leftrightarrow$ $[\begin{array}{l} x + 2 = 0 \\ x - 1 = 0 \end{array}$

$\Leftrightarrow$ $[\begin{array}{l} x = - 2 \\ x = 1 \end{array}$

Vậy S = {1;-2}

Câu 23:

16/07/2024

Số nghiệm của phương trình:

(x² + 9)(x – 1) = (x² + 9)(x + 3) là

A. 2

B. 1

C. 0

D. 3

Xem đáp án

Đáp án: C

Giải thích:

Lời giải

Ta có (x² + 9)(x – 1) = (x² + 9)(x + 3)

$\Leftrightarrow$ (x² + 9)(x – 1) - (x² + 9)(x + 3) = 0

$\Leftrightarrow$ (x² + 9)(x – 1 – x – 3) = 0

$\Leftrightarrow$ (x² + 9)(-4) = 0

$\Leftrightarrow$ x² + 9 = 0

$\Leftrightarrow$ x² = -9 (vô nghiệm)

Vậy tập nghiệm của phương trình S = Ø

hay phương trình không có nghiệm

Câu 24:

15/07/2024

Nghiệm nhỏ nhất của

phương trình (2x + 1)² = (x – 1)² là

A. 0

B. 2

C. 3

D. -2

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

Ta có (2x + 1)² = (x – 1)²

$\Leftrightarrow$ (2x + 1)² - (x – 1)² = 0

$\Leftrightarrow$ (2x + 1 + x – 1)(2x + 1 – x + 1) = 0

$\Leftrightarrow$ 3x(x + 2) = 0

$\Leftrightarrow$ $[\begin{array}{l} 3 x = 0 \\ x + 2 = 0 \end{array}$

$\Leftrightarrow$ $[\begin{array}{l} x = 0 \\ x = - 2 \end{array}$

Vậy tập nghiệm của phương trình S = {0; -2}

Nghiệm nhỏ nhất là x = -2

Câu 25:

23/07/2024

Nghiệm nhỏ nhất của phương trình

${(- \frac{1}{2} x + 1)}^{2} = {(\frac{3}{2} x - 1)}^{2}$ là

A. 0

B. 2

C. 3

D. -2

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3