Trắc nghiệm Toán 8 Bài 3: Phương trình đưa về được dạng ax + b
-
369 lượt thi
-
20 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
22/07/2024
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Ta có x – 12 = 6 – x
⇔ x + x = 6 + 12
⇔2x = 18
⇔ x = 18 : 2
⇔x = 9
Vậy phương trình có nghiệm x = 9
Câu 2:
17/07/2024 Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Ta có 2x – 3 = 12 – 3x
⇔2x + 3x = 12 + 3
⇔5x = 15
⇔x = 15 : 5
⇔ x = 3
Vậy phương trình có một nghiệm duy nhất x = 3
Câu 3:
19/07/2024Gọi x0 là một nghiệm của
phương trình 5x – 12 = 4 - 3x.
Hỏi x0 còn là nghiệm của phương trình nào dưới đây?
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
5x – 12 = 4 - 3x
⇔ 5x + 3x = 4 + 12
⇔8x = 16
⇔x = 2
Do đó phương trình có nghiệm x0 = 2.
Đáp án A: Thay x0 = 2 ta được 2.2 – 4 = 0
nên x0 = 2 là nghiệm của phương trình.
Câu 4:
22/07/2024Phương trình
x−1277+x−1178=x−7415+x−7316 có nghiệm là
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
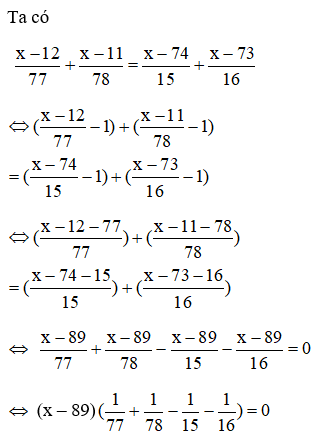
Câu 5:
20/07/2024Phương trình
x−277+x−178=x−745+x−736 có nghiệm là
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
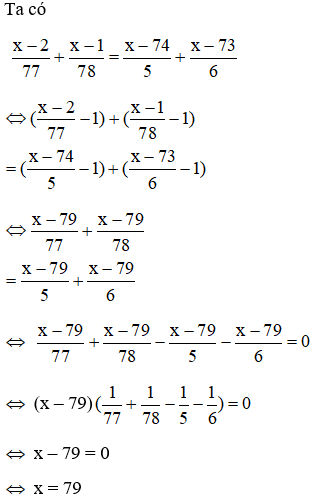
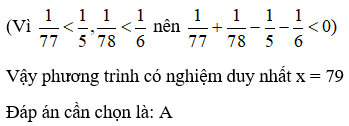
Câu 6:
19/07/2024Tính tổng các nghiệm của phương trình
|3x + 6| - 2 = 4, biết phương trình có 2 nghiệm phân biệt.
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
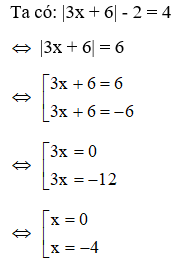
Vậy tổng các nghiệm của phương trình là 0 + (-4) = -4
Câu 7:
23/07/2024Nghiệm của phương trình
x+ab+c+x+ba+c+x+ca+b=−3 là
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
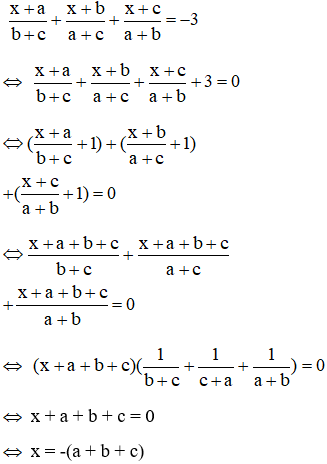
Vậy phương trình có nghiệm x = -(a + b + c)
Câu 8:
16/07/2024Số nghiệm nguyên dương của
phương trình 4|2x – 1| - 3 = 1 là:
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
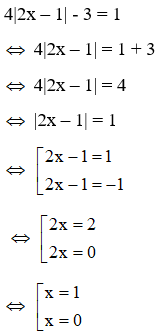
Do x nguyên dương nên phương trình
chỉ có một nghiệm x = 1 nguyên dương
Câu 9:
16/07/2024 Xem đáp án
Đáp án: A
Giải thích:
Lời giải
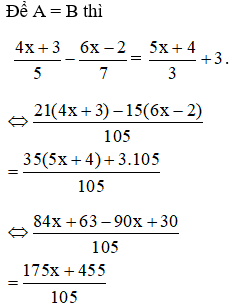
⇔ 84x + 63 - 90x + 30 = 175x + 455
⇔ 84x – 90x – 175x = 455 – 30 – 63
⇔ -181x = 362
⇔ x = -2
Vậy để A = B thì x = -2
Câu 10:
22/07/2024Gọi x0 là nghiệm của phương trình
3(x – 2) – 2x(x + 1) = 3 – 2x2. Chọn khẳng định đúng
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
3(x – 2) – 2x(x + 1) = 3 – 2x2
⇔3x – 6 – 2x2 – 2x = 3 – 2x2
⇔x – 6 – 2x2 – 3 + 2x2 = 0
⇔x – 9 = 0
⇔x = 9
Vậy nghiệm của phương trình
x0 = 9 là số nguyên dương
Câu 11:
22/07/2024Gọi x0 là nghiệm của phương trình
2.(x – 3) + 5x(x – 1) = 5x2. Chọn khẳng định đúng.
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
2.(x – 3) + 5x(x – 1) = 5x2
⇔ 2x – 6 + 5x2 – 5x = 5x2
⇔5x2 – 5x2 + 2x – 5x = 6
⇔ -3x = 6
⇔x = -2
Vậy nghiệm của phương trình là x0 = -2 > -3
Câu 12:
18/07/2024Kết luận nào sau đây là đúng nhất khi nói về nghiệm x0 của phương trình
x+12+x+34=3−x+23
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
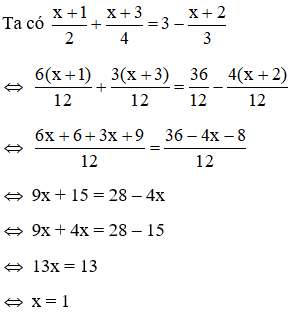
Vậy nghiệm phương trình là x = 1 là số nguyên dương
Câu 13:
16/07/2024Cho hai phương trình 7(x – 1) = 13 + 7x (1)
và (x + 2)2 = x2+ 2x + 2(x + 2) (2). Chọn khẳng định đúng
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Ta có
7(x – 1) = 13 + 7x
⇔7x – 7 = 13 + 7x
⇔7x – 7x = 13 + 7
⇔0 = 20 (VL)
Vậy phương trình đã cho vô nghiệm
Lại có:
(x + 2)2 = x2+ 2x + 2(x + 2)
⇔x2 + 4x + 4 = x2 + 2x + 2x + 4
⇔x2 + 4x – x2 – 2x – 2x = 4 – 4
⇔0 = 0
Điều này luôn đúng với mọi x thuộc R
Vậy phương trình đã cho vô số nghiệm
Câu 14:
16/07/2024Kết luận nào sau đây là đúng nhất khi nói
về nghiệm x0 của phương trình
x+12+x+34=3−x+23
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
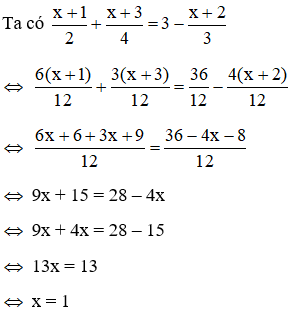
Vậy nghiệm phương trình là x = 1
là không số nguyên tố cũng không là hợp số
Câu 15:
20/07/2024Cho hai phương trình 3(x – 1) = -3 + 3x (1)
và (2 – x)2 = x2 + 2x – 6(x + 2) (2). Chọn khẳng định đúng
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Ta có
3(x – 1) = -3 + 3x
⇔3x – 3 = -3 + 3x
⇔3x – 3x = -3 + 3
⇔0x = 0
Điều này luôn đúng với mọi x thuộc R
Vậy phương trình đã cho vô số nghiệm
Lại có
(2 – x)2 = x2 + 2x – 6(x + 2)
⇔4 – 4x + x2 = x2 + 2x – 6x – 12
⇔x2 – x2 – 4x – 2x + 6x + 4 + 12 = 0
⇔16 = 0 (vô lí)
Vậy phương trình đã cho vô nghiệm
Do đó (1) vô số nghiệm, (2) vô nghiệm
Câu 16:
23/07/2024Gọi x1 là nghiệm của phương trình
x3 + 2(x – 1)2 – 2(x – 1)(x + 1) = x3 + x – 4 – (x – 4)
và x2 là nghiệm của phương trình .
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
+ Ta có
x3 + 2(x – 1)2 – 2(x – 1)(x + 1) = x3 + x – 4 – (x – 4)
⇔x3 + 2(x – 1)2 – 2(x – 1)(x + 1) – x3 – x + 4 + (x – 4) = 0
⇔ (x3 – x3) + 2(x2 – 2x + 1) – 2(x2 – 1) – x + 4 + x – 4 = 0
⇔ 2x2 – 4x + 2 – 2x2 + 2 – x + 4 + x – 4 = 0
⇔(2x2 – 2x2) + (-4x – x + x) + (2 + 2 + 4 – 4) = 0
⇔ -4x + 4 = 0
⇔ -4x = -4
⇔x = 1
Suy ra x1 = 1
+ Ta có:
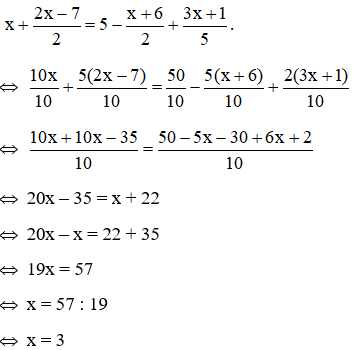
Suy ra x2 = 3
Nên x1.x2 = 1.3 = 3
Câu 17:
16/07/2024Gọi x1 là nghiệm của
phương trình (x + 1)3 – 1 = 3 – 5x + 3x2 + x3
và x2 là nghiệm của phương trình 2(x – 1)2 – 2x2 + x – 3 = 0
Giá trị S = x1 + x2 là:
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
+ Ta có: (x + 1)3 – 1 = 3 – 5x + 3x2 + x3
⇔x3 + 3x2 + 3x + 1 – 1 = 3 – 5x + 3x2 + x3
⇔x3 – x3 + 3x2 – 3x2 + 3x + 5x – 3 = 0
⇔8x – 3 = 0
⇔ x = 38
Suy ra x1 =38
+ Ta có: 2(x – 1)2 – 2x2 + x – 3 = 0
⇔2(x2 – 2x + 1) – 2x2 + x – 3 = 0
⇔2x2 – 4x + 2 – 2x2 + x – 3 = 0
⇔-3x – 1 = 0
⇔ x = -13
Suy ra x2 =-13
Nên x1+x2=38+(−13)=124
Câu 18:
23/07/2024 Xem đáp án
Đáp án: B
Giải thích:
Lời giải
x – 3 = -x + 2
⇔x – 3 + x – 2 = 0
⇔2x – 5 = 0
⇔x = 52
Vậy phương trình có tập nghiệm S = {52}
Câu 19:
19/07/2024 Xem đáp án
Đáp án: A
Giải thích:
Lời giải
5 – x2 = -x2 + 2x – 1
⇔5 – x2 + x2 - 2x + 1 = 0
⇔-2x + 6 = 0
⇔-2x = -6
⇔x = 3
Vậy phương trình có nghiệm x = 3
Câu 20:
16/07/2024 Xem đáp án
Đáp án: B
Giải thích:
Lời giải
(x – 1)2 = x2 + 4x – 3
⇔x2 – 2x + 1 = x2 + 4x – 3
⇔x2 – 2x + 1 – x2 – 4x + 3 = 0
⇔-6x + 4 = 0
⇔x =23
Vậy phương trình có nghiệm duy nhất x =23